計數排序,桶排序,基數排序,
計數排序->桶排序->基數排序,三者的排序思想是相通的,是逐漸複雜,使用性更廣的.(個人理解,歡迎指正,wiki上說基數排序是桶排序的變形,兩者的方法相似,都是分配和收集.百度百科說基數排序又叫bucket sort,基數在這裡個人理解就是基座,如果當前數的要分配的那一位與基座一致,就放進對應基座的桶內)
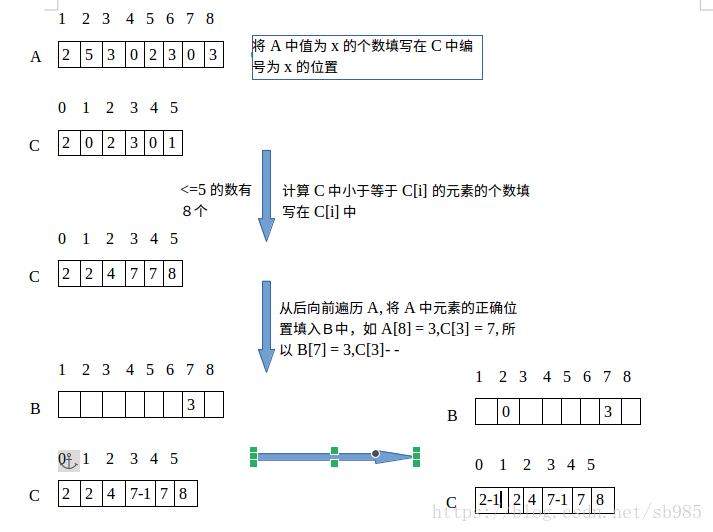
計數排序
計數排序是一種根據小整數鍵對一組物件進行排序的演算法,使用鍵值作為陣列中的索引,因此它不是比較排序,它是一個整數排序演算法。它通過計算具有每個不同鍵值的物件的數量並使用這些計數的算術來確定輸出序列中每個鍵值的位置。計數排序只適合元素是整數,小規模的排序
counting_sort(A 桶排序
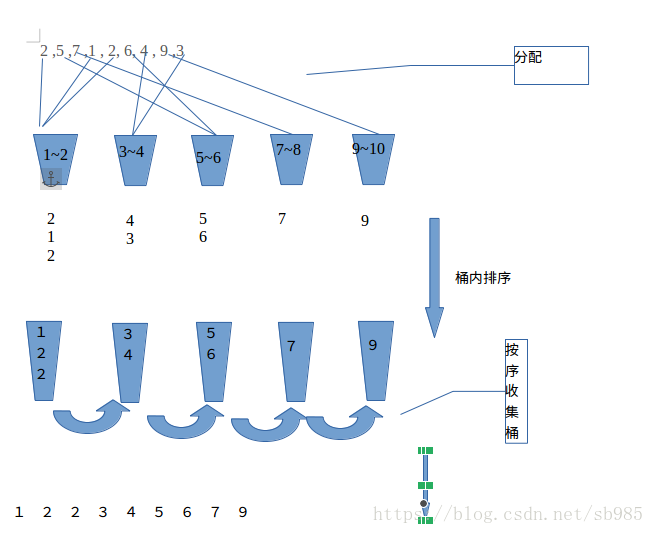
桶排序或桶排序是一種排序演算法,它通過將陣列元素分配到多個桶中來工作。然後,使用不同的排序演算法或遞迴應用桶排序演算法,將每個桶單獨排序。
基數排序
wilki百科解釋:
基數排序是一種非比較性的整數排序演算法,它使用整數鍵對資料進行排序,方法是將鍵分組為具有相同重要位置和值的單個數字。需要位置表示法,但由於整數可以表示字串(例如,名稱或日期)和特殊格式的浮點數,所以基數排序不限於整數。
least significant digit (LSD) 基數排序通常使用以下排序順序:短鍵(長度短)在較長的鍵之前,而長度相同的鍵按字典順序排序。這與整數表示的正常順序一致,例如順序1,2,3,4,5,6,7,8,9,10,11。從個位開始向高位挪動
most significant digit (MSD)基數排序使用詞典順序,這適合排序字串,如單詞或固定長度整數表示。諸如“b,c,d,e,f,g,h,i,j,ba”的序列按字典順序排序為“b,ba,c,d,e,f,g,h,i,j ”。如果使用詞典排序來對可變長度整數表示進行排序,則從1到10的數字的表示將被輸出為1,10,2,3,4,5,6,7,8,9,如同較短的按鍵左對齊,並在右側用空白字元填充以使短按鍵與最長按鍵一樣長,以確定排序順序。從高位向地位開始比較,MSD的方式與LSD相反,是由高位數為基底開始進行分配,但在分配之後並不馬上合併回一個數組中,而是在每個“桶子”中建立“子桶”,將每個桶子中的數值按照下一數位的值分配到“子桶”中,在進行完最低位數的分配後再合併回單一的陣列中。
LSD:

1.DataDefinition.h
//鏈式基數排序
const int RADIX = 10;
//對於基數排序只能是int 元素型別
typedef int ArrType[RADIX];
ArrType f,e;
template <class T>
struct SLCell{//SLCell is a number
T *keys;//一個數的各個位
int next;
};
template <class T>
struct SLList{
SLCell<T> *SList;//將輸入數依次連線起來
int keynum;
int recnum;
};
template <class T>
void OutPut(SLList<T> &SL){
for(int i = SL.SList[0].next;i;i=SL.SList[i].next){
for(int j = 1;j <= SL.keynum;j++){
cout <<SL.SList[i].keys[j];//輸出數字的每一位
}//endfor
cout<<"\t";
}//endfor
cout<<endl;
}
#endif
2.RadixSort.h
#ifndef __RADIXSORT__
#define __RADIXSORT__
#include "DataDefinition.h"
template <class T>
void InitSLList(SLList<T> &SL){
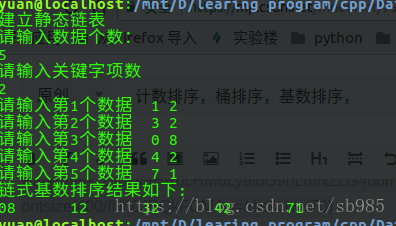
//建立靜態連結串列
cout<<"建立靜態連結串列"<<endl<<"請輸入資料個數:"<<endl;
cin >>SL.recnum;
SL.SList = new SLCell<T>[SL.recnum+1];
cout<<"請輸入關鍵字項數"<<endl;
cin >>SL.keynum; //關鍵字的位數,也是基的個數
//建立基,SL.SList[i]是輸入第i個數,SList[i].key[j]是第i個數的第j位
for(int i = 1;i <= SL.recnum; ++i){
//為每個數建立keynum位,因為下標j從1開始,所以建立keynum+1個元素的陣列
SL.SList[i].keys = new T[SL.keynum+1]; //建立一個桶(基),以i為基底
}//endfor
//輸入資料
SL.SList[0].next = 1;
for(int i = 1;i <= SL.recnum; ++i){
cout<<"請輸入第"<<i<<"個數據 ";
for(int j = 1;j <= SL.keynum; j++){
//輸入數字的每一位
cin>>SL.SList[i].keys[j];
}//endfor
//連線各個基底
if (i != SL.recnum) {
SL.SList[i].next = i+1;
} else {
SL.SList[i].next = 0;
}
}//endfor
}
template <class T>
void RelList(SLList<T> &SL){
//Release distributed space
for(int i = 1;i <= SL.recnum; ++i){
delete SL.SList[i].keys;
}//endfor
delete SL.SList;
}
template <class T>
void Distribute(SLCell<T> *r,int i,ArrType &f,ArrType &e){
//按第i個關鍵字s[i]建立RADIX個子表,使同一子表中記錄的keys[i]相同
//f[0..RADIX]和e[0..RADIX]分別指向各個子表中第一個和最後一個記錄
int j;
//初始化RADIX個基底
for(j = 0;j < RADIX; ++j){
f[j] = 0;
}//endfor
for(int a = r[0].next;a;a = r[a].next){
//r[0].next is the first radix,the last's next is 0
//r[i] 是一個數,按照第i位進行分配,j是數r[a]的第i位的值
j = r[a].keys[i];
if(!f[j]){ //如果基數為j的桶為空,則將這個數的序號放進桶中,否則就新增在原始鏈的後面
f[j] = a; //這一步只代表該基底有數,且存放連結串列的首地址,原序列中的第a個數
} else {
r[e[j]].next = a; //把原待排序數字序列中基底為j的最後一個數的下一個元素是當前元素a
}
e[j] = a; //e記錄基為j的桶中最後放入的數在原序列中的序號
}
}
template <class T>
void Collect(SLCell<T>*r,int i,ArrType &f,ArrType &e){
//按keys[i]自小到大將f[0...RADIX]所指各個子表依次連結成一個連結串列
int j;
for(j=0;!f[j];++j); //找第一個非空子表,(非空桶)j是桶的編號
r[0].next = f[j]; //r[0].next指向第一個非空子表中的第一個結點
int t = e[j]; //基數為j的桶最後放入的數序號
while(j < RADIX){
for(j++;j<RADIX-1 && !f[j];j++);//找下一個非空子表
if(f[j]){
r[t].next = f[j]; //連結兩個非空子表
t = e[j]; //記錄當前基底的最後一個數的序號,方便與下一個非空桶連結
}
}//endwhile
r[t].next = 0; //t指向最後一個非空子表中的左後一個結點
}
template <class T>
void RadixSort(SLList<T> &SL){
//對L做基數排序,使得L按關鍵字自小到大有序
for(int i = SL.keynum;i>=1;i--){//按最高位優先依次對各位進行分配和收集
Distribute(SL.SList,i,f,e); //第i趟分配,按照第i位分配
Collect(SL.SList,i,f,e); //第i趟收集
}//endfor
}
#endif
3.RadixMain.cpp
#include <iostream>
using namespace std;
#include "DataDefinition.h"
#include "RadixSort.h"
int main(int argc, char* argv[]){
SLList<int> SL;
InitSLList(SL);
RadixSort(SL);
cout<<"鏈式基數排序結果如下:"<<endl;
OutPut(SL);
RelList(SL);
return 0;
}