桶排序：

要排序的資料有n個，均勻地劃分到m個桶內，每個桶裡就有k=n/m個元素。每個桶內部使用快速排序，時間複雜度為O(k*logk)。m個桶排序的時間複雜度是O(m*k*logk)，因為k=n/m，所以整個桶排序的時間複雜度就是O(n*log(n/m))。當桶個數m接近資料個數n時，log(n/m)就是一個非常小的常量，這個時候桶排序的時間複雜度接近O(n)。

如果有些桶內的資料非常多，有些非常少，很不均勻，那桶內資料排序的時間複雜度就不是常量級了。在極端情況下，如果資料都被劃分到一個桶內，那就退化為O(nlogn)的排序演算法。

計數排序：

計數排序只能用在資料範圍不大的場景中，如果資料範圍k比要排序的資料n大很多，就不適合計數排序了。而且，計數排序只能給非負整數排序，如果要排序的資料是其他型別的，就要在不改變大小的情況下，轉化為非負整數。

#include<iostream>
#include<stdlib.h>

using namespace std;

int main()
{
    int n;
    cin >> n;
    int *a = new int[n];
    int *c = new int[n];
    memset(a, 0, n*sizeof(int));
    memset(c, 0, n*sizeof(int));
    int max = 0;
    for (int i = 0; i < n; i++)
    {
        cin >> a[i];
        max = a[i]>max ? a[i] : max;
    }
    int *b = new int[max+1];
    memset(b, 0, (max+1)*sizeof(int));
    for (int i = 0; i < n; i++)
    {
        b[a[i]]++;
    }
    for (int i = 1; i < max + 1; i++)
    {
        b[i] = b[i] + b[i - 1];
    }
    for (int i = 0; i < n; i++)
    {
        b[a[i]]--;
        c[b[a[i]]] = a[i];
    }
    for (int i = 0; i < n; i++)
        cout << c[i] << endl;
    delete[]a;
    delete[]b;
    delete[]c;

    return 0;
}
 

基數排序：

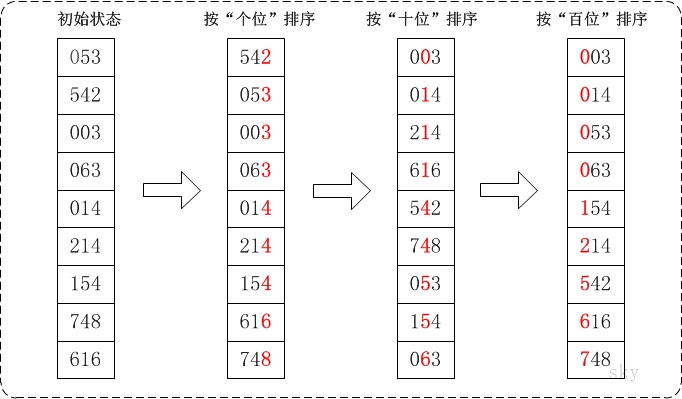
基數排序對每個要排序的數分段排序，基數排序每次排序必須是穩定的，否則這個實現思路是不正確的。因為如果是非穩定演算法，那最後一次排序只會考慮最高位的大小順序，完全不管其他位的大小關係，那麼低位的排序就完全沒有意義了。

基數排序對要排序的資料時有要求的，需要可以分割出獨立的“位”來比較，而且位之間有遞進的關係，如果a資料的高位比b資料大，那剩下的低位就不用比較了。除此之外，每一位的資料範圍不能太大，要可以線性排序演算法來排序，否則，基數排序的時間複雜度就無法做到O(n)了。

int GetMaxDigit(int* arr, size_t n)
{
	assert(arr);
	int digit = 1;
	int base = 10;
	for (size_t i = 0; i < n; i++)
	{
		while (arr[i] >= base)
		{
			++digit;
			base *= 10;
		}
	}
	return digit;
}
 
void LSDSort(int* arr,size_t n)
{
	assert(arr);
	int base = 1;
	int digit = GetMaxDigit(arr, n);
	int* tmp = new int[n];
	while (digit--)
	{
		int count[10] = { 0 };
		//統計某一位出現相同數字的個數
		for (size_t i = 0; i < n; i++)
		{
			int index = arr[i] / base % 10;
			count[index]++;
		}
		int start[10] = { 0 };
		//統計個位相同的數在陣列arr中出現的位置
		for (size_t i = 1; i < n; i++)
		{
			start[i] = count[i - 1] + start[i - 1];
		}
		//初始化tmp陣列
		memset(tmp, 0, n*sizeof(int));
		//從桶中重新排序資料
		for (size_t i = 0; i < n; ++i)
		{
			int index = arr[i] / base % 10;
			tmp[start[index]++] = arr[i];
		}
		//將tmp陣列中的元素拷回原陣列
		memcpy(arr, tmp, n*sizeof(int));
		base *= 10;
	}
	delete[] tmp;
}