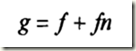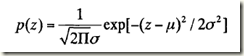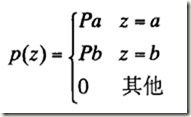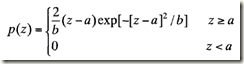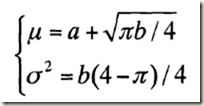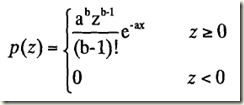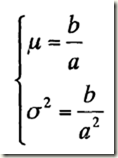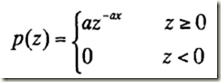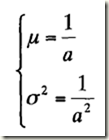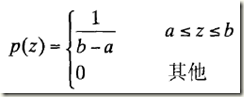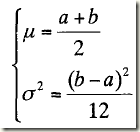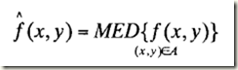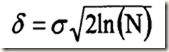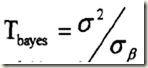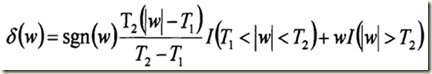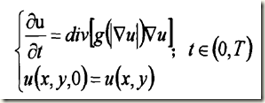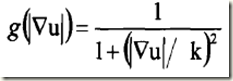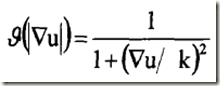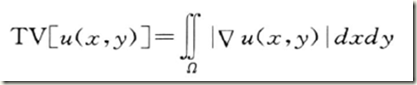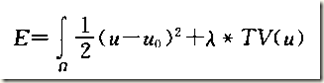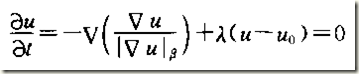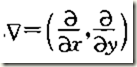一，背景

隨著各種數字儀器和數碼產品的普及，影象和視訊已成為人類活動中最常用的資訊載體，它們包含著物體的大量資訊，成為人們獲取外界原始資訊的主要途徑。然而在影象的獲取、傳輸和存貯過程中常常會受到各種噪聲的干擾和影響而使影象降質，並且影象預處理演算法的好壞又直接關係到後續影象處理的效果，如影象分割、目標識別、邊緣提取等，所以為了獲取高質量數字影象，很有必要對影象進行降噪處理，儘可能的保持原始資訊完整性（即主要特徵）的同時，又能夠去除訊號中無用的資訊。所以，降噪處理一直是影象處理和計算機視覺研究的熱點。

影象視訊去噪的最終目的是改善給定的影象，解決實際影象由於噪聲干擾而導致影象質量下降的問題。通過去噪技術可以有效地提高影象質量，增大信噪比，更好的體現原來影象所攜帶的資訊，作為一種重要的預處理手段，人們對影象去噪演算法進行了廣泛的研究。在現有的去噪演算法中，有的去噪演算法在低維訊號影象處理中取得較好的效果，卻不適用於高維訊號影象處理；或者去噪效果較好，卻丟失部分影象邊緣資訊，或者致力於研究檢測影象邊緣資訊，保留影象細節。如何在抵制噪音和保留細節上找到一個較好的平衡點，成為近年來研究的重點。

二，影象去噪理論基礎

2.1 影象噪聲概念

噪聲可以理解為“妨礙人們感覺器官對所接收的信源資訊理解的因素”。例如，一幅黑白圖片，其平面亮度分佈假定為f(x，y)，那麼對其接收起干擾作用的亮度分佈R(x，y)，即可稱為影象噪聲。但是，噪聲在理論上可以定義為“不可預測，只能用概率統計方法來認識的隨機誤差”。因此將影象噪聲看成是多維隨機過程是合適的，因而描述噪聲的方法完全可以借用隨機過程的描述，即用其概率分佈函式和概率密度分佈函式。但在很多情況下，這樣的描述方法是很複雜的，甚至是不可能的。而實際應用往往也不必要。通常是用其數字特徵，即均值方差，相關函式等。因為這些數字特徵都可以從某些方面反映出噪聲的特徵。

2.2 常見的影象噪聲

在我們的影象中常見的噪聲主要有以下幾種：

（1），加性噪聲

加性嗓聲和影象訊號強度是不相關的，如影象在傳輸過程中引進的“通道噪聲”電視攝像機掃描影象的噪聲的。這類帶有噪聲的影象g可看成為理想無噪聲影象f與噪聲n之和，即：

（2），乘性噪聲

乘性嗓聲和影象訊號是相關的，往往隨影象訊號的變化而變化，如飛點掃描影象中的嗓聲、電視掃描光柵、膠片顆粒造成等，這類噪聲和影象的關係是：

（3），量化噪聲

量化嗓聲是數字影象的主要噪聲源，其大小顯示出數字影象和原始影象的差異，減少這種嗓聲的最好辦法就是採用按灰度級概率密度函式選擇化級的最優化措施。

（4），“椒鹽”噪聲

此類嗓聲如影象切割引起的即黑影象上的白點，白影象上的黑點噪聲，在變換域引入的誤差，使影象反變換後造成的變換噪聲等。

2.3 影象噪聲模型

實際獲得的影象含有的噪聲，根據不同分類可將噪聲進行不同的分類。從噪聲的概率分情況來看，可分為高斯噪聲、瑞利噪聲、伽馬噪聲、指數噪聲和均勻噪聲。它們對應的概率密度函式（PDF）如下：

（1），高斯噪聲

在空間域和頻域中，由於高斯噪聲在數學上的易處理性，這種噪聲(也稱為正態噪聲)模型經常被用在實踐中。高斯隨機變數Z的PDF由下式給出：

其中，z表示灰度值，μ表示z的平均值或期望值，α表示z的標準差。當z服從上述分佈時，其值有95%落在[(μ-2σ)， (μ+2σ)]範圍內。

（2）脈衝噪聲（椒鹽噪聲）

（雙極）脈衝噪聲的PDF可由下式給出：

如果b>a，則灰度值b在影象中將顯示為一個亮點，反之則a的值將顯示為一個暗點。若Pa或Pb為零，則脈衝稱為單極脈衝。如果Pa和Pb均不可能為零，尤其是它們近似相等時，則脈衝噪聲值將類似於隨機分佈在影象上的胡椒和鹽粉微粒。由於這個原因，雙極脈衝噪聲也稱為椒鹽噪聲。

（3）瑞利噪聲

其均值和方差分別為：

（4）伽馬噪聲

其密度的均值和方差為：

（5）指數分佈噪聲

其中a>0，概率密度函式的期望值和方差是：

（6）均勻噪聲

其均值和方差分別為：

2.4 影象去噪演算法分類

（1），空間域濾波

空域濾波是在原影象上直接進行資料運算，對畫素的灰度值進行處理。常見的空間域影象去噪演算法有鄰域平均法、中值濾波、低通濾波等。

（2），變換域濾波

影象變換域去噪方法是對影象進行某種變換，將影象從空間域轉換到變換域，再對變換域中的變換系數進行處理，再進行反變換將影象從變換域轉換到空間域來達到去除影象嗓聲的目的。將影象從空間域轉換到變換域的變換方法很多，如傅立葉變換、沃爾什-哈達瑪變換、餘弦變換、K-L變換以及小波變換等。而傅立葉變換和小波變換則是常見的用於影象去噪的變換方法。

（3），偏微分方程

偏微分方程是近年來興起的一種影象處理方法，主要針對低層影象處理並取得了很好的效果。偏微分方程具有各向異性的特點，應用在影象去噪中，可以在去除噪聲的同時，很好的保持邊緣。偏微分方程的應用主要可以分為兩類:一種是基本的迭代格式，通過隨時間變化的更新，使得影象向所要得到的效果逐漸逼近，這種演算法的代表為Perona和Malik的方程[27]，以及對其改進後的後續工作。該方法在確定擴散係數時有很大的選擇空間，在前向擴散的同時具有後向擴散的功能，所以，具有平滑影象和將邊緣尖銳化的能力。偏微分方程在低噪聲密度的影象處理中取得了較好的效果，但是在處理高噪聲密度影象時去噪效果不好，而且處理時間明顯高出許多。

（4），變分法

另一種利用數學進行影象去噪方法是基於變分法的思想，確定影象的能量函式，通過對能量函式的最小化工作，使得影象達到平滑狀態，現在得到廣泛應用的全變分TV模型就是這一類。這類方法的關鍵是找到合適的能量方程，保證演化的穩定性，獲得理想的結果。

（5），形態學噪聲濾除器

將開與閉結合可用來濾除噪聲，首先對有噪聲影象進行開運算，可選擇結構要素矩陣比噪聲尺寸大，因而開運算的結果是將背景噪聲去除；再對前一步得到的影象進行閉運算，將影象上的噪聲去掉。據此可知，此方法適用的影象型別是影象中的物件尺寸都比較大，且沒有微小細節，對這類影象除噪效果會較好。

三，幾種影象去噪演算法介紹

3.1 基於空間域的中值濾波

中值濾波器是一種常用的非線性平滑濾波器，基本原理是把數字影象或數字序列中一點的值用該點鄰域內各點的中值代換。設f(x，y)表示數字影象畫素點(x，y)的灰度值，濾波視窗為A的中值濾波器可以定義為：

當n為奇數時，n個數x1，x2，…xn的中值就是按數值大小順序處於中間的數；當n為偶數時，我們定義兩個中間數平均值為中值。

3.2 基於小波域的小波閾值去噪

小波萎縮法是目前研究最為廣泛的方法，小波萎縮法又分成如下兩類：第1類是閾值萎縮，由於閾值萎縮主要基於如下事實，即比較大的小波係數一般都是以實際訊號為主，而比較小的係數則很大程度是噪聲。因此可通過設定合適的閾值，首先將小於閩值的係數置零，而保留大於閉值的小波係數；然後經過閾值函式對映得到估計係數；最後對估計係數進行逆變換，就可以實現去噪和重建；而另外一種萎縮方法則不同，它是通過判斷係數被噪聲汙染的程度，併為這種程度引入各種度量方法(例如概率和隸屬度等)，進而確定萎縮的比例，所以這種萎縮方法又被稱為比例萎縮。閾值萎縮方法中的兩個基本要素是閾值和閾值函式。

閾值的選擇：

閾值的確定在閾值萎縮中是最關鍵的。目前使用的閾值可以分成全域性閾值和區域性適應閾值兩類。其中，全域性閾值對各層所有的小波係數或同一層內的小波係數都是統一的；而區域性適應閾值是根據當前係數周圍的區域性情況來確定閾值。目前提出的全域性閾值主要有以下幾種：

（1），Donoho和Johastone統一閾值（簡稱DJ閾值）：

其中σ為噪聲標準方差，N為訊號的尺寸或長度。

（2），基於零均值正態分佈的置信區間閾值：

（3），Bayes Shrink閾值和Map Shrink閾值。在小波係數服從廣義高斯分佈的假設下，Chang等人得出了閾值：

其中，（R為噪聲標準方差，RB為廣義高斯分佈的標準方差值）。

（4），最小最大化閾值：這是Donoho和John Stone在最小最大化意義下得出的閾值與上邊的閾值不同，它是依賴於訊號的，而且沒有顯式表示式，在求取時需要預先知道原訊號。

（5），理想閾值：理想閾值是在均方差準則下的最優閾值，同最大最小化閾值一樣，也沒有顯式的表示式，並且這個閾值的計算通常也需先知道訊號本身。

閾值函式：

Bruce和Gao。提出了一種半軟閾值函式：

該方法通過選擇合適的閾值T1和12，可以在軟閾值方法和硬閾值方法之間達到很好的折中。另外，zhang等人為了對SIJRE誤差準則函式進行基於梯度的優化搜尋，提出了另外一種閾值函式，這種閾值函式同上邊閉值函式所不同的是它擁有更高的導數階，故其重建影象更為平滑，但該文作者將去噪效果的提高歸功於搜尋方法，其實，Donoh。和 Johnstone提出的在當前小波係數集合中，搜尋最優閾值的方法，對於當前已經是優的了，由此可見，該去噪效果的提高則應歸功於閾值函式的選取。

3.3 基於PDE的影象去噪

目前，基於PDE的影象處理方法的研究，也是影象去噪的研究熱點方向，並且己經取得了一定的理論和實際應用方面的成它的去噪過程為通過建立噪聲影象為某非線性PDE的初始條件，然後求解這個PDE，得到在不同時刻的解，即為濾波結果。Perona和Malik提出了基於PDE的非線性擴散濾波方法（以下簡稱P-M），各向異性的去噪模型根據影象的梯度值決定擴散的速度，使之能兼顧噪聲消除和邊緣保持兩方面的要求。

以P-M模型為代表的這類方法己經在影象增強、影象分割和邊緣檢測等領域得到了廣泛的應用，取得了很好的效果。

P-M是一種非線性的各向異性方法，目的是為了克服線性濾波方法存在的模糊邊緣和邊緣位置移動的缺點。基本思想是:影象特徵強的地方減少擴散係數，影象特徵弱的地方增強擴散係數。方程如下：

其中u(x，y，t)是隨時間變化的影象，是梯度的模，擴散係數函式用於控制擴散速度。理想的擴散係數應當使各向異性擴散在灰度變化平緩的區域快速進行，而在灰度變化急劇的位置（即影象特徵處）低速擴散乃至不擴散函式，所以，應具有如下性質：

基於以上的兩個性質，P-M提出瞭如下擴散係數函式：

其中k為邊緣閾值，用來判斷邊緣區域和平坦區域。引入通量函式，主要是為了闡明閾值k在擴散操作中的作用，其函式定義如下：

儘管P-M方程在抑制噪聲與保留影象重要特徵方面取得了一定的效果，但卻表現出病態且不穩定。Catt等人對該方程進行了改進，他們先用高斯核同影象作卷積，然後取其梯度模作影象邊緣資訊的估計。文獻提出用優化的對稱指數濾波器對影象作光滑，然後取其梯度模作影象邊緣資訊的估計。這兩種估計方法的基本思想是降低噪聲的干擾，更加真實地提取影象的邊緣特徵資訊，以便利用邊緣資訊更好地控制P-M方程的擴散行為。

3.4 全變分（TV）影象去噪

TV方法是由Rudin Osher and Fatemi提出，它基於變分法的思想，確定影象的能量函式，通過對影象能量函式最小化達到平滑去噪的目的。是現在比較流行的影象復原方法。影象的能量函式方程為：

在文獻[2]中給出的全變分去噪能量泛函為：

為了使得能量函式最小，其尤拉-拉格朗日方程為：

其中，梯度運算元：

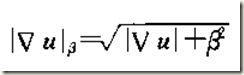
正則項：

用來減少平坦區域的退化。將整體左邊轉換成影象中任意畫素點中的區域性座標系後，方程可以分解成邊緣方向和邊緣正交的兩個方向，分解後個方向的係數控制著該方向的擴散強度。擴散方向實際上是一個分線性的各向異性的擴散方程，其擴散運算元僅沿影象梯度的正交方向擴散，擴散係數為1/|▽μ|，而朝著梯度方向無擴散。這樣可以通過影象的梯度來判斷邊緣位置，使得邊緣擴散係數最小，從而降低對邊緣的模糊程度，但是也由於邊緣的擴散係數小，噪聲得不到很好的抑制，而且當|▽μ|>λ的時候，勢能函式是非凸的，使得邊緣處處理表現不穩定。所以，如何確定擴散引數的值是一個問題。

四，總結

隨著科技的發展和工作生活的需要，數字影象濾波應用將越來越廣泛，要求也將越來越高。到目前為止，仍有很多去噪方面的新思想、新方法出現，不斷的充實影象去噪方法。而且，噪聲的研究範圍也在不斷擴大，由高斯噪聲到非高斯噪聲。去噪技術有很廣泛的應用和研究的前景，而且，研究領域也在不斷的拓展。

本文主要的內容是對影象的去噪技術做一個簡單的介紹。全文對影象去噪技術進行了概述，包括噪聲的概念和去噪原理，並對一些基本的影象去噪方法做了介紹。由於時間關係，並且這是導論課程的論文作業，就沒有進行深入細緻的研究。

五，參考文獻

[1] GonzalesRC，WoodsRE.DigitalImageProeessing，SeeondEdition Beijing Eleetronieand Industrial Press，2002

[2] Leonid I. Rudin 1, Stanley Osher and Emad Fatemi Nonlinear total variation based noise removal algorithms 1992

[3] W.Luo，An efficient detail preserving approach for removing impulse noise in images，IEEE Signal Proeess.Lett.，2006，13(7):413-416.

From

擴充套件閱讀