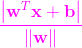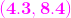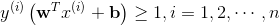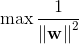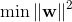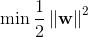支援向量機(support vector machine)--模型的由來
1995年,Corinna Cortes(CC老師)靚照
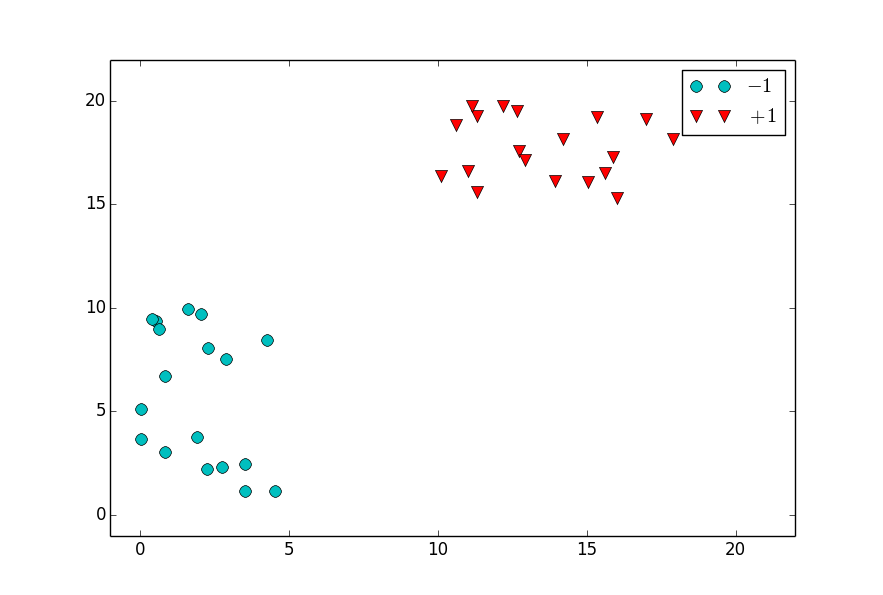
CC老師首先給出資料集是二分類且線性可分的情況,設是





CC老師提出了第一個問題:既然能線性可分,那麼就有超平面
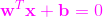
我和同學A、同學B分別給出了直線的方程,我求出的直線方程是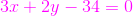


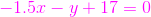
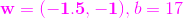
CC老師向我們提出了第二個問題,既然這三個方程只代表一條直線,能不能想個辦法,把這條直線統一一下,標準一下,CC老師看出了我們三個的迷惑,就給我提示了一下,他說你們可以找到離這條直線最近的點,通過這個點改進你們的直線方程。
補充幾何知識:
第一個知識點:已知超平面
,哪個一點離這條超平面最近,答案:哪一個點使得
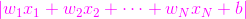
第二個知識點:已知超平面

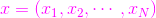
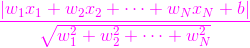
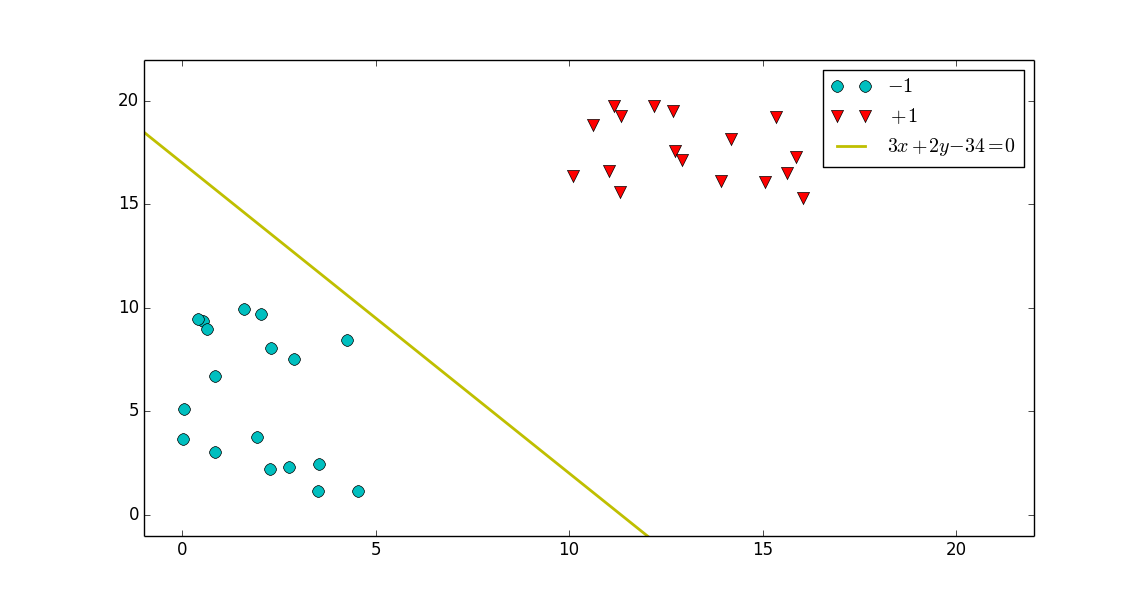
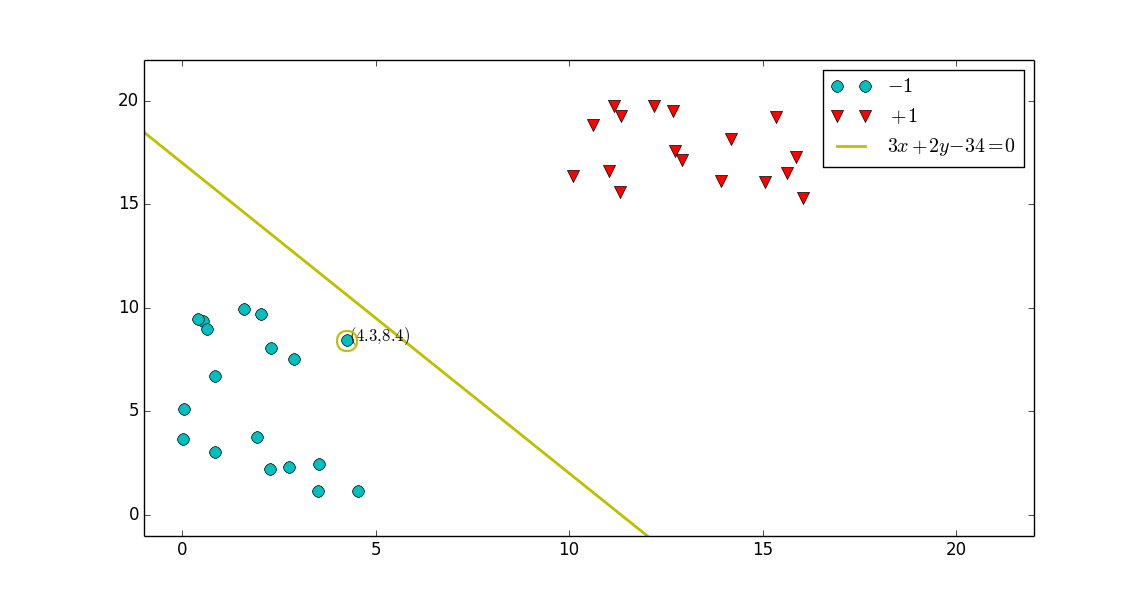
通過幾何知識,我修改我的直線方程,在二維平面裡可直觀的看到離這黃色直線最近的點,我用黃色圓圈標註出來了,並給出了這個點的座標
我的直線方程改進過程: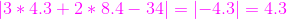

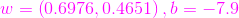
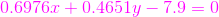
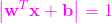
,都有
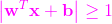
同學B改進他的直線方程過程(我偷瞄的):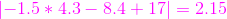
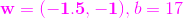
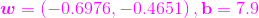

同學A改進他的方程,按照上述步驟,最後和我的是一樣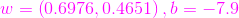
然後,我們三個把各自的答案給了CC老師,老師看後說,你們的給出的直線方程使得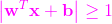
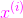
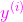

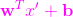
則對於直線當直線方程是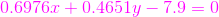
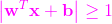

而當直線方程是
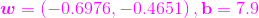
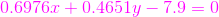

 ,直到現在我們三個終於把這條直線的直線方程給統一化了,即
,直到現在我們三個終於把這條直線的直線方程給統一化了,即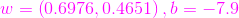


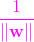
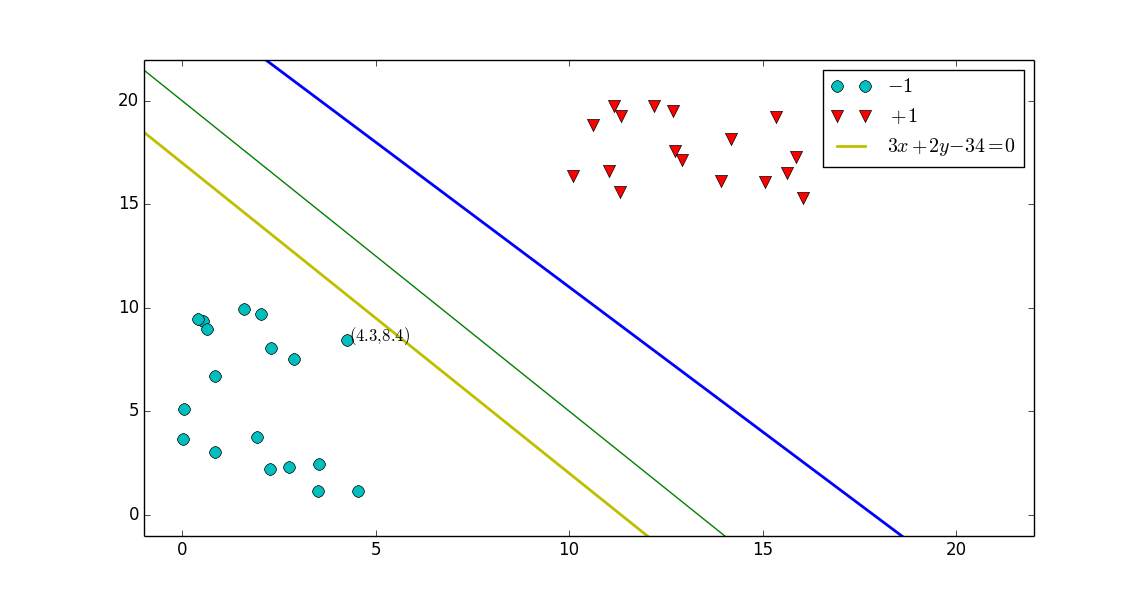
CC老師又拋給了我們一個問題,還有沒有別的超平面可以分開這兩個資料集,回答是肯定,會有無數個超平面分開這兩個資料集,
按照求統一黃色直線方式,我們又求出了圖中綠色和藍色的直線方程,其中綠色直線方程的的係數為我們用綠色的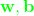
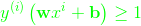
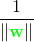
表示,且滿足
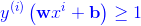
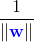

老師又著急了,既然有無數條,就是有無數個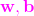

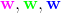
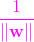


老師說你們能不能用"選資料集到直線 最小距離最大的那一個" 這句話抽象出一個模型或者公式,老師提示說用運籌學分支之一非線性規劃的知識,歸納一下這個模型,我們想了一想給出了這個模型公式:
老師微微點點頭,範數的平方好處理一些吧,再改改,我們修改如下:
然後,老師說原問題一般用最小值處理,我們又做了一下修改:
最後把原問題乘以0.5,最優化問題的解不變,所以最後模型為:
老師最後微笑了一下,說下課吧,你們的模型已經解釋出來了!我們著急的拉住CC老師說:老師,我們穿越過來不容易,你直接告訴我們,這個模型有無數個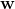
本集結束!
下集預告:又要穿越去找Harold W. Kuhn和Albert W. Tucker,去學習他們的解非線性規劃的kuhn-Ticker條件(KKT)。
對於支援向量機比較好開源庫是臺灣大學林老師寫的libsvm,這個庫只有常用的三個核函式,我在原始碼的基礎上,加上了十個核函式。。。