同餘方程組，中國剩餘定理（孫子定理）學習

從孫子定理介紹起把，其實對於它的由來大家還是很有興趣瞭解一下的。
以下是我取於互動百科的內容：
中國南北朝時期（5～6世紀）著名的著作《孫子算經》中“物不知數”問題所闡述的定理。物不知數問題的原題是：“今有物，不知其數，三三數之剩二，五五數之剩三，七七數之剩二，問物幾何？”這屬於數論的一次同餘方程組問題。用現代數學符號可表為求下列同餘方程的整數解：


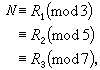
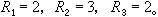
《孫子算經》沒有給出具體演算法。宋代秦九韶在《數書九章》中第一次詳細地、完整地闡述了求解一次同餘方程組的演算法，他稱做“大衍總數術”，其中包括求kj的一種機械化演算法──大衍求一術。

個人認為孫子定理理解起來還是挺困難的，不真正理解原理，只是一味套模版並沒有什麼用，非常容易忘記，所以好好學吧。

孫子定理又名中國剩餘定理，其實就是求 模線性方程組 其 x 值。
x ≡ a1 ( % n1);
x ≡ a2 ( % n2);
x ≡ a3 ( % n1);
……
求其值要滿足一系列的模線性方程，具我知道的可以說有4種方法。
1. 列舉法。
列舉滿足每個方程的一系列數字，找到滿足各個方程的數字（既各個方程都有的數字）。
注：個人不細講，因為這個方法好理解，而且可以說這只是個理論成立，對於現實裡由於複雜度大，並不適用。

2. 化為同餘數法
如果把上述的模線性方程組的mod值化成相同是不是簡單許多。秉著這個思想：
X≡2 (mod 7 ) ； X≡5 (mod 9 ) ；X≡1 (mod 5 )
這三個同餘式，餘數不同，分別為7、9、5，為了能利用同餘式的和差特性，簡化計算，先設法使它們的除數相同，為此：
X≡2 (mod 7 )兩邊都乘9* 5，得X* 45≡2* 45 (mod 7* 45 ) →45 X≡90 (mod 315 ) …(1)
X≡5 (mod 9 ) 兩邊都乘7* 5，得X* 35≡5* 35 (mod 9* 35 ) →35 X≡175 (mod 315 ) …(2)
X≡1 (mod 5 ) 兩邊都乘7* 9，得X* 63≡1* 63 (mod 9* 63 ) →63 X≡ 63 (mod 315 ) …(3)
(1)＋(2)＋(3)＝ (4) → 143 X≡328 (mod 315 ) …4)
根據同餘式的加減性質，(1)＋(2)＋(3)得：
143 X≡328 (mod 315 ) 即 143 X≡13 (mod 315 )
再最後單獨求解一個同餘方程，用擴充套件歐幾里德很快得出。
注：個人認為雖然這個方法好理解，也簡單。但如果 ni 夠大，方程夠多，最後的mod數很大而難以實現原來的效果。

3. 逐級滿足法
見名思意，逐級滿足。這個方法的基本思路是：
這裡我把x用C來代寫以免於下面x,y整數解衝突，下面整數解用x,y是讓學過擴充套件歐幾里德的人更好的理解。總的來說，它要求把第一和第二方程合併，再把合併方程和第三個方程再合併，知道合併完全。先解算出合符第一個方程的C（注意C是滿足現在這級的C，所以C在不斷滿足的過程中變化）。再解算出合符第一、第二個方程的C，【過程：對於頭兩個關係式，C % n1==a1, C % n2==a2，可以聯立方程組 n1* x+n2* y==a2-a1 ，很熟悉，直接套用擴充套件歐幾里得演算法得到一組解x,y，再取x的最小值，帶入式子C%n1==a1(化為不定方程)中，便得到了答案 C 。】求出了合併方程的C，那麼合併方程的n怎麼求？
答案是 n = lcm(n1,n2)。
新式子公式是這樣的：c mod lcm(n1,n2) ==C 這裡C是要求的新答案，C是前兩個式子求的的一個解，lcm(n1,n2)是a1，a2的最小公倍數。
你可以理解為新的答案C即要mod n1,又要modn2,所以就mod lcm(n1,n2)。而餘數C 是剛前面求得的答案，也就是說c不管怎麼折騰，都還會保留一個C，即不會破壞前面的成果！

//MOD[]為ni;
//c[]為ai; 這裡因為x≡ai (%ni)就為 x + ni*y = ai;作為不定方程ax + by = c來看，ai就為ci。
            int now_mod = MOD[0]; //n1第一個方程
            int now_c = c[0];     //a1第一個方程
            for(int i = 1; i < 4; i++)
            {
//n1*x+n2*y==a2-a1,這裡由於在用擴充套件歐幾里德時,a,b會變化,   所以再引用了變數now_mod。下面只作方程一和二的講解
                int a = now_mod;  //n1
                int b = MOD[i];   //n2
                int c_real = c[i] - now_c; //a2-a1
                int x,y;
                int d = exgcd(a,b,x,y);
                x = x * c_real/d;
                int r = b/d;
                x = (x%r+r)%r;    //得到最小正的x。
                now_c = now_mod * x + now_c; //變化的C
                now_mod = now_mod * (MOD[i]/d); //變化的n
        //得到第一和第二合併的式子就是 c（這個其實無所謂，重點在下面倆的變化） ≡ now_c (mod now_mod)
            }
            int ans = now_c;

注：在我看來這個演算法最實用，雖然演算法難了點，但它可以在
gcd（ni,n(i-1)） == 任何數 適用，而下面我們介紹的賊難的“大衍求一術”解法只適用與 ni 互質。

4. 大衍求一術法
X≡R1 (mod m1 ) X≡2 (mod 7 )
X≡R2 (mod m2) X≡5 (mod 9 )
X≡R3 (mod m3) X≡1 (mod 5 )
名詞註釋及計算步驟：
1 餘數R：R1=2、R2=5、R3=1
2 模，亦即除數m：例中m1=7、m2=9、m3=5
3 模的最小公倍數G：G=m1* m2* m3，例中M=7* 9* 5=315
4 衍數（區域性公倍數）y：Y1=m2m3、Y2=m1m3，Y3=m1m2，例中Y1=9* 5=45、Y2=7* 5=35、Y3=7* 9=63
5 乘率：(衍數*乘率)除以模(除數)，而餘數為1。即：
衍數 * 乘率 ≡ 1 (mod m)，乘率C可以經過反算而得到。
（要求的）X ≡ Σ 餘數* 衍數* 乘率 (mod G)。
注：案例是拿的，原理不知，條件是互質，感覺還是挺麻煩的額。