粒子群演算法 MATLAB
阿新 • • 發佈:2019-02-08
對於Ackley函式粒子群演算法求解其全域性最優值,是粒子群演算法應用的一個典型例子
Ackley函式形如下
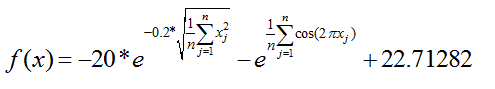
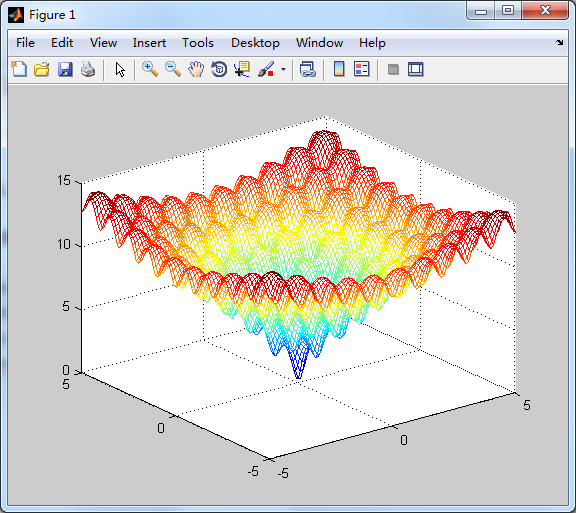
藉助matlab畫出函式影象如下
clear all;clc;
a=linspace(-5,5,100);
b=linspace(-5,5,100);
[x,y]=meshgrid(a,b);
z=-20*exp(-0.2*sqrt(0.5*(x.^2+y.^2)))-exp(0.5*(cos(2*pi*x)+cos(2*pi*y)))+22.71282;
mesh(x,y,z)顯然函式在(0,0)處可以取得最小值,接下來藉助PSO演算法求解此最小值點所在座標,具體程式碼如下:
clear all;clc; Gk=200;%設定迭代次數 scale=100;%設定粒子種群規模 wini=0.9;%慣性因子 wend=0.4; m=5*(2*rand(2,scale)-1);%粒子群初始化位置 z=zeros(1,scale); x=zeros(1,scale); y=zeros(1,scale); for i=1:scale x(i)=m(1,i); y(i)=m(2,i); z(i)=-20*exp(-0.2*sqrt(0.5*(x(i)^2+y(i)^2)))-exp(0.5*(cos(2*pi*x(i))+cos(2*pi*y(i))))+22.71282; end x=[x;y];%每個粒子座標 xmax=0.0002;%確定x飛行方向速度最大值 ymax=0.0002;%確定y飛行方向速度最大值 v=zeros(2,scale);%初始化粒子群速度為零 pbest=100*ones(1,scale);%初始化各個粒子最優值 pbest_zuobiao=ones(2,scale);%初始化各個粒子最佳位置座標 gbest=100;%初始化整個粒子群最優數值 gbest_zuobiao=[5;5];%初始化整個粒子群最優位置 for g=1:Gk for j=1:scale if z(j)<pbest(j)%如果粒子發現更好位置 pbest(j)=z(j);%更新粒子最優值 %更新粒子最佳位置座標 pbest_zuobiao(1,j)=x(1,j); pbest_zuobiao(2,j)=x(2,j); end end for j=1:scale if gbest>pbest(j)%如果種群發現更優位置 gbest=pbest(j);%求出種群最佳位置 gbest_zuobiao=[pbest_zuobiao(1,j);pbest_zuobiao(2,j)];%種群中最佳位置座標 end end for j=1:scale w=(wini-wend)*(Gk-g)/Gk+wend; %更新每個粒子移動速度 v(:,j)=w*v(:,j)+2*rand()*(pbest_zuobiao(:,j)-x(:,j))+2*rand()*(gbest_zuobiao-x(:,j)); %x、y軸方向飛行速度不能超過限定最大值0.0002 if v(1,j)>xmax v(1,j)=xmax; else if v(1,j)<-xmax v(1,j)=-xmax; end end if v(2,j)>ymax v(2,j)=ymax; else if v(2,j)<-ymax v(2,j)=-ymax; end end p=x+v; %x、y軸方向飛行不能超過邊界最大值5 for k=1:scale if p(1,j)>5 x(1,j)=5; else if p(1,j)<-5 x(1,j)=-5; else if p(2,j)>5 x(2,j)=5; else if p(2,j)<-5 x(2,j)=-5; else x=p;%x、y軸方向飛行都沒有超過邊界最大值5 end end end end end %更新每個粒子適應度值 z(j)=-20*exp(-0.2*sqrt(0.5*(x(1,j)^2+x(2,j)^2)))-exp(0.5*(cos(2*pi*x(1,j))+cos(2*pi*x(2,j))))+22.71282; end end gbest gbest_zuobiao