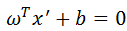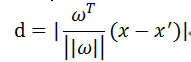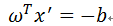超平面詳解-SVM支援向量機
研究了半天,終於對“超平面”有了個初步瞭解。
n 維空間中的超平面由下面的方程確定:
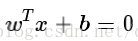
其中,w 和 x 都是 n 維列向量,x 為平面上的點,w 為平面上的法向量,決定了超平面的方向,b 是一個實數,代表超平面到原點的距離。且
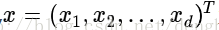
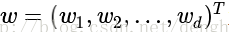
那麼,w 為什麼是法向量呢?b 為什麼表示平面到原點的距離呢?下面給出詳細解釋:
我們對“平面”概念的理解,一般是定義在三維空間中的,即

這個平面由兩個性質定義:1、方程是線性的,是由空間點的各分量的線性組合。2、方程數量是1。這個平面是建立在“三維”上的。如果我們撇開“維度”這個限制,那麼就有了超平面的定義。實際上,超平面是純粹的數學概念,不是物理概念,它是平面中的直線、空間中的平面的推廣,只有當維度大於3,才稱為“超”平面。它的本質是自由度比空間維度小1。自由度的概念可以簡單的理解為至少要給定多少個分量的值才能確定一個點. 例如, 三維空間裡的(超)平面只要給定了(x,y,z)中任意兩個分量, 剩下的一個的值就確定了. 先確定值的兩個分量是自由的, 因為它們想取什麼值就能取什麼值;剩下的那個是"不自由的", 因為它的值已經由另外兩確定了. 二維空間裡的超平面為一條直線. 一維空間裡超平面為數軸上的一個點。
百度百科上對超平面的數學定義是這樣的:超平面H是從n維空間到n-1維空間的一個對映子空間,它有一個n維向量和一個實數定義。因為是子空間,所以超平面一定過原點。
通常,R2(二維空間)中的點集 i = (x,y)滿足等式 (點集 i 實際為一條直線):
ax + 1/by + c = 0 (1) (這裡使用1/b 是為了後續計算好表示)
其中,a,b,c均為標量,a,1/b至少有一個不為0.我們假設 b 不為0。,那麼
y = -abx - cb
此時,使用換元法,令 t = x,(顯然,t 為標量) 則點集 i (x,y) 可以表示成
i (x,y) = ( t, -abt - cb) = t (1, -ab) + (0, -cb)
這條直線是什麼?實際上就是過 (0, -cb) 點,方向為 (1, -ab) 的直線 L。
進一步,我們令向量 n = (a,1/b),則 (1)可以表示成n* i + c = 0 (2)
神奇的一刻來臨了。假設在直線 L 上取一點 p0(x0,y0),顯然,n* p0 + c = 0,那麼 c = -n* p0.
更進一步,將 (2)改寫,可得 n* i-n* p0 = 0 ,即可 n* (i - p0 ) = 0。
因為 n 和(i - p0 ) 均是向量,(i - p0 ) 在直線 L 上, 所以,n 垂直直線L ,即n為直線L 的法向量。更進一步,我們可以得到,那些與p的差向量與 n 向量正交的點,就是點集 i (x,y).
進一步解釋什麼是超平面:
給定向量空間 Rn 中的一個點 P 和一個非零向量n ,滿足
n * (i - p)= 0
則稱點集 i 為通過點p 的超平面,向量 n為通過超平面的法向量。按照這個定義,雖然當維度大於3才可以成為“超”平面,但是你仍然可以認為,一條直線是 R2 空間內的超平面,一個平面是 R3 空間內的超平面 。Rn 空間的超平面是Rn 空間內的一個 n - 1 維的仿射子空間。
點到超平面的距離
樣本空間中的任意一點 x,到超平面(w,b)的距離,可以表示為
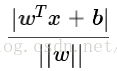
後來有同學評論說,點到超平面上的點為什麼這麼計算呢?我在這裡再具體說一下。推導過程並不繁瑣(這裡以三維空間為例)。
對於超平面A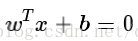
對於空間上任意一點 x, 到平面 A 的距離 H,等於 x 到超平面的法向量長度,也就是 向量 xx' 在垂直方向上(即法向量)上的投影。而計算投影,將 xx' 乘以法向量 w 即可。並且,我們不光要投影,還要計算單位,即使用單位為 1 的投影。也就是在分母除以 || w ||。所以,距離 H 可以表示為:
又因為:
所以,距離為:
判斷超平面的正反
一個超平面可以將它所在的空間分為兩半, 它的法向量指向的那一半對應的一面是它的正面, 另一面則是它的反面。如果利用數學來判斷的話,需要利用到法向量 w。

若將距離公式中分子的絕對值去掉, 讓它可以為正為負. 那麼, 它的值正得越大, 代表點在平面的正向且與平面的距離越遠. 反之, 它的值負得越大, 代表點在平面的反向且與平面的距離越遠。