當我們使用正則化的線性迴歸方法預測房價時，發現得到的模型應用於新的資料上時有很大誤差，這時，我們可以選擇一些解決方案，例如：

上圖中的這六種解決方案都有相應的條件，如圖中藍色字型所示。

【一、迴歸模型選擇】

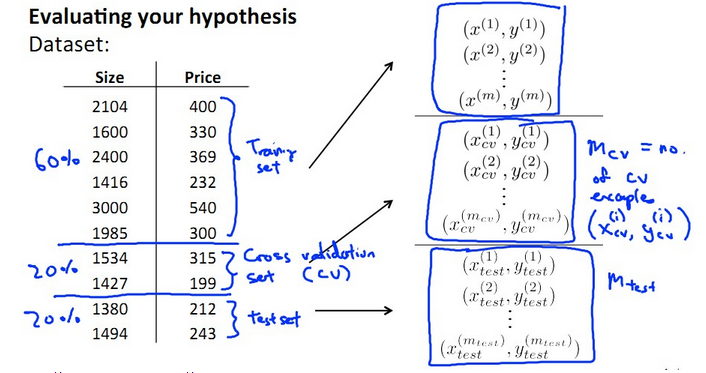
我們引入一類資料集，叫做cross validation set，即交叉驗證資料集。將所有資料按6：2：2
分為training set , cross validation set , testing set三類，如下圖所示：

【模型選擇的步驟】

1. 建立d個假設模型，如下圖所示（d=10），分別在training set 上求使其training error最小的θ向量，那麼得到d個θ。
2. 對這d個假設模型，在cross validation set上計算J(cv)，選擇cv set error最小的一個模型 ，例如：如果J(cv)在第2組中最小，則取d=2的假設。
   

【二、bias and variance的定義】

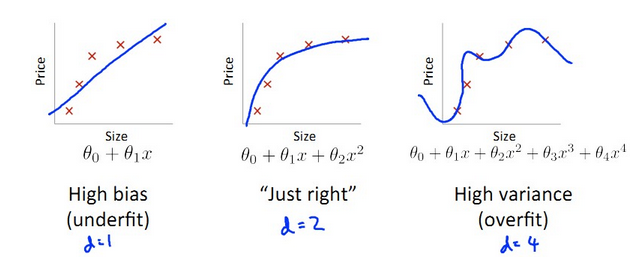
對於不同的模型，有不同的擬合情況，如下圖所示：

由上圖可定義：

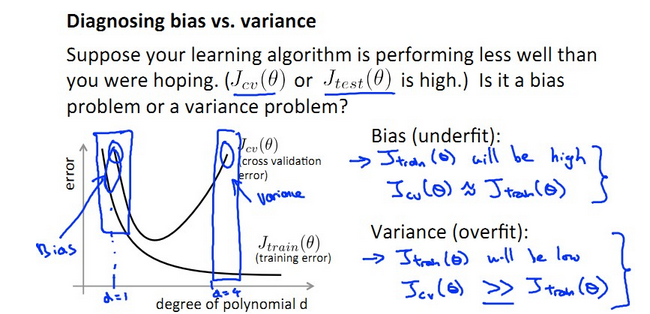
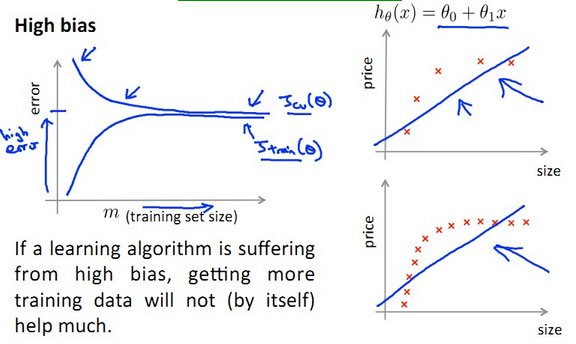
• bias：J(train)大，J(cv)大，J(train)≈J(cv)，bias產生於d小，underfit階段
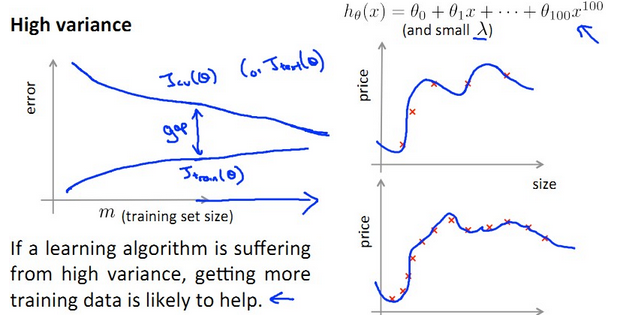
• variance：J(train)小，J(cv)大，J(train)遠遠小於J(cv)，variance產生於d大，overfit階段

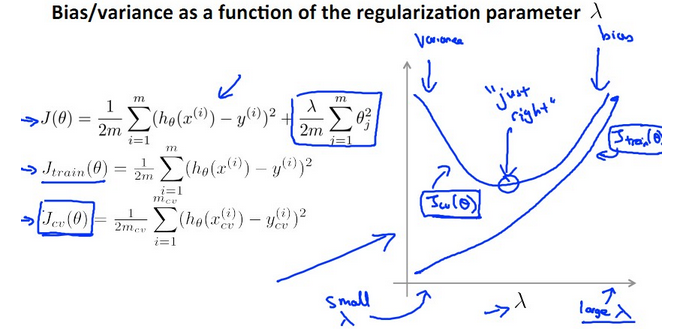
【三、正則化引數λ的選擇】

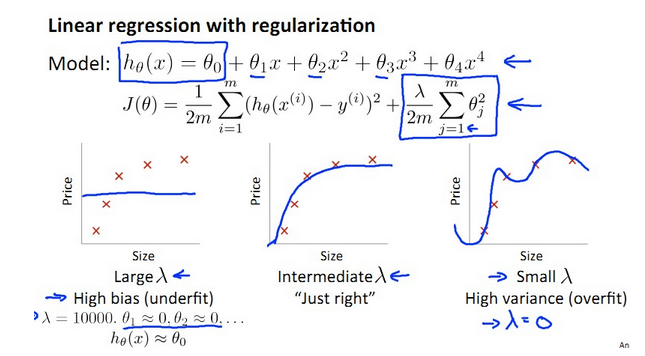
為了解決過擬合的問題，使用正則化，但是正則化引數λ的正確選擇是一個難題。

• λ太小導致overfit，產生variance，J(train)遠遠小於J(cv)

• λ太大導致underfit，產生bias，J(train) ≈ J(cv)

  如下圖所示：
  

關於λ的曲線如下：

【引數λ的選擇】

1. 將λ從0，0.01，一直往上每次乘以2，那麼到10.24總共可以試12次λ。這12個λ會得到12個模型，如下圖所示。每個對應有J(θ)和 Jcv(θ)，分別在training set 上求使其training error最小的θ向量，那麼得到12個θ。
   2.在cross validation set上計算J(cv)，選擇cv set error最小的一個模型 ，然後取出令Jcv（θ）最小的一組定為最終的λ。例如假設J(cv)在第5組中最小，則取λ=0.08的假設，如下圖所示。

【四、什麼時候增加訓練資料training set才是有效的？】

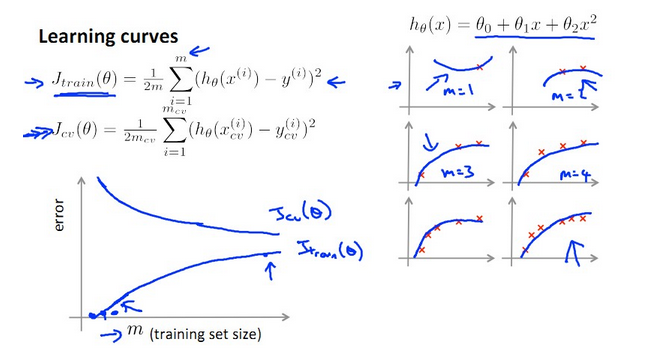
從上圖可知：訓練資料越少，J(train)越小，J(cv)越大；m越大，J(train)越大（因為越難完全擬合），J(cv)越小（因為越精確）。

那麼怎麼判斷增加訓練資料training set的數目m能夠對演算法有較大改進呢？？

【總結】

• Underfit 的 High bias: J(train)≈J(cv)增加m沒什麼幫助！
• Overfit的 High Variance: 增加m使得J(train)和J(cv)之間gap減小，有助於performance提高！