0 概率&概率圖模型

世界的真實狀態幾乎無法通過我們有限的觀測完全確定下來，因為大多數關係根本就是非確定性的，至少相對於我們對其的建模能力而言。不確定性的出現源於我們對世界的觀察能力有限，對其建模的能力有限，甚至可能源於其固有的不確定性。由於這種關於真實世界狀態的普遍且根本的不確定性的存在，需要我們的推理系統考慮不同的可能性。為了得到有意義的結論，我們不僅需要推理什麼是可能的（possible），而且需要推理什麼是很可能的（probable）[1]
概率論運算為我們考慮多個可能的結果及其可能性提供了一種形式框架。它定義了一組互斥且無窮盡的可能時間，並賦予每種可能事件一個概率。概率論可以用兩個簡單的方程表示（加和規則和乘積規則）。

1 貝葉斯網路

1.1 鏈式法則與貝葉斯公式

條件概率鏈式法則：
P(A1A2...An)=P(A1)P(A2|A1)...P(An−1|A1A2,,,An−2)P(An|A1A2...An−1)
貝葉斯公式：
P

1.2 簡單的圖模型表示

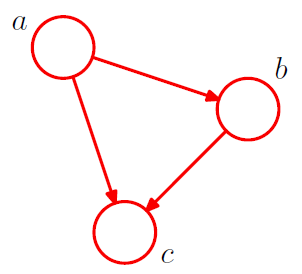
為了理解有向圖對於描述概率分佈的作⽤，⾸先考慮三個變數a; b; c上的⼀個任意的聯合分佈p(a; b; c)。注意，現階段我們不需要對這些變數做出任何更多的假設，例如它們是離散的還是連續的。實際上，圖模型的⼀個強⼤的⽅⾯是，⼀個具體的圖可以描述⼀⼤類概率分佈。通過使⽤概率的乘積規則，我們可以將聯合概率分佈寫成下⾯的形式。
p(a,b,c)=p(c|a,b)p(a,b)=p(c|a,b)p(b|a)p(a)
關於上式，很有趣的⼀點是，它的左側關於三個變數a; b; c是對稱的，⽽右側不是。
實際上，通過對左邊的分解，我們隱式地選擇了⼀個特定的順序（即a; b; c）。如果選擇⼀個不同的順序，我們會得到⼀個不同的分解⽅式，因此就得到⼀個不同的圖表⽰形式。
注意，這個分解⽅法對於任意的聯合概率分佈的選擇都成立。現在，我們使⽤⼀個簡單的圖模型表示方程的右側：

N個變數的聯合概率分佈

根據1.1中的條件概率鏈式法則
P(A1A2...An)=P(A1)P(A2|A1)...P(An−1|A1A2,,,An−2)P(An|A1A2...An−1)
我們將1.2中的簡單的例子擴充套件到N個變數的聯合概率分佈P(A1A2...An)
對應⼀個給定的N，我們可以將其表⽰為⼀個具有N個結點的有向圖，每個結點對應於上式右側的⼀個條件概率分佈，每個結點的輸⼊連結包括所有以編號低於當前結點編號的結點為起點的連結。我們說，這個圖是全連線的（fully connected），因為每對結點之間都存在⼀個連結。

1.3 缺失連線圖

⽬前為⽌，我們操作的物件是⼀個完全⼀般的聯合概率分佈，從⽽分解⽅式以及對應的全連線圖表⽰，可以應⽤於概率分佈的任意選擇。正如我們將會看到的，真正傳遞出圖表⽰的概率分佈的性質的有趣資訊的是圖中連結的缺失（absence）。考慮下圖。這不是⼀個全連線的圖，因為從x1到x2或者從x3到x7之間不存在連結。

現在，我們將根據這幅圖，寫出對應的聯合概率表示式。聯合概率表示式由⼀系列條件概率的乘積組成，每⼀項對應於圖中的⼀個結點。每個這樣的條件概率分佈只以圖中對應結點的⽗結點為條件。例如，x5以x1和x3為條件。於是，7個變數的聯合概率分佈為
p(x1)p(x2)p(x3)p(x4|x1,x2,x3)p(x5|x2,x3)p(x6|x4)p(x7|x4,x5)
條件概率鏈式法則和貝葉斯網路鏈式法則差異，比較這個式子和條件概率鏈式法則的差異

1.4有向圖模型的聯合概率分佈的分解屬性

由上面的論述我們可以知道，給定的有向圖和變數上對應的概率分佈之間的⼀般關係。在圖的所有結點上定義的聯合概率分佈由每個結點上的條件概率分佈的乘積表⽰，每個條件概率分佈的條件都是圖中結點的⽗結點所對應的變數。因此，對於⼀個有K個結點的圖，聯合概率為
p(x)=∏Kk=1p(xk|pak)
其中，pak表示xk父節點的集合，x={x1,x2,...xk}

注：我們考慮的有向圖要滿⾜⼀個重要的限制，即不能存在有向環（directed cycle）。換句話說，在圖中不能存在這樣的路徑：從某個結點開始，沿著連結中箭頭的⽅向運動，結束點為起點。這種沒有有向環的圖被稱為有向⽆環圖（directed acyclic graph），或者DAG。這等價於存在⼀個將誒點的排序，使得不存在從某個結點到序號較⼩的結點的連結。

1.5 條件獨立

2 馬爾科夫隨機場

3 因子圖

From:

Ref:
[1] Probabilistic Graphical Models Principles and Techniques. Daphne Koller,Nir Friedman
[2] Pattern Recognition and Machine Learning. Chapter 8
[3] http://www.cnblogs.com/bhlsheji/p/4875551.html