支援向量機(SVM)必備知識(KKT、slater、對偶)
SVM目前被認為是最好的現成的分類器,SVM整個原理的推導過程也很是複雜啊,其中涉及到很多概念,如:凸優化問題、拉格朗日乘子法、對偶問題,slater條件、KKT條件還有複雜的SMO演算法!相信有很多研究過SVM的小夥伴們為了弄懂它們也是查閱了各種資料,著實費了不少功夫!本文便針對SVM涉及到的這些複雜概念進行總結,希望為大家更好地理解SVM奠定基礎。
一、凸集和凸函式
在講解凸優化問題之前我們先來了解一下凸集和凸函式的概念
凸集:在點集拓撲學與歐幾里得空間中,凸集是一個點集,其中每兩點之間的直線上的點都落在該點集中。千言萬語不如一張圖來的明白,請看下圖:

凸函式:一個定義在向量空間的凸子集C(區間)上的實值函式f,如果在其定義域C上的任意兩點x,y以及t∈[0,1]有

則該函式為凸函式!凸函式另一個判別方式是:如果一個凸函式是一個二階可微函式,則它的二階導數是非負的。上圖:

下面引自維基百科:
注意:中國大陸數學界某些機構關於函式凹凸性定義和國外的定義是相反的。Convex Function在某些中國大陸的數學書中指凹函式。Concave Function指凸函式。但在中國大陸涉及經濟學的很多書中,凹凸性的提法和其他國家的提法是一致的,也就是和數學教材是反的。舉個例子,同濟大學高等數學教材對函式的凹凸性定義與本條目相反,本條目的凹凸性是指其上方圖是凹集或凸集,而同濟大學高等數學教材則是指其下方圖是凹集或凸集,兩者定義正好相反。 另外,也有些教材會把凸定義為上凸,凹定義為下凸。碰到的時候應該以教材中的那些定義為準。
在機器學習領域大多數是採用上文中所描述的凸函式和凹函式的定義,下文中凸函式的定義也採用上文描述的那種!
二、凸優化問題
凸優化:凸優化是指一種比較特殊的優化,是指求取最小值的目標函式為凸函式的一類優化問題。其中,目標函式為凸函式且定義域為凸集的優化問題稱為無約束凸優化問題。而目標函式和不等式約束函式均為凸函式,等式約束函式為仿射函式,並且定義域為凸集的優化問題為約束優化問題。
上面是來自百度百科定義,下面我們對其總結,將其公式化!
凸優化性質:
1、目的是求取目標函式的最小值;
2、目標函式和不等式約束函式都是凸函式,定義域是凸集;
3、若存在等式約束函式,則等式約束函式為仿射函式;
4、對於凸優化問題具有良好的性質,區域性最優解便是全域性最優解。
一個凸優化問題用公式描述為:

所以其目標函式f(x)以及不等式約束條件g(x)便是凸函式,而等式約束條件h(x)是仿射函式。
大家可能要問:何為仿射函式!!!
仿射函式:即是deg(h(x))=1的函式,常數項為0的仿射函式稱為線性函式。
其中符號 deg() 表示多項式h(x)的次數<將函式看成多項式而已
三、拉格朗日乘子法
拉格朗日乘子法的作用:求函式f(x1,x2…)在g(x1,x2…)=0的約束條件下的極值。
拉格朗日乘子法的操作過程
1、定義新函式:

2、利用偏導方式列出以下方程
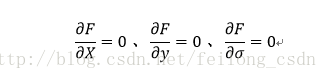
3、求解出x,y,σ的值帶入F(x,y,σ)便是目標函式的極值
四、對偶問題,slater條件,KKT條件
這裡我們來談一談SVM中必須需要明白的對偶問題,要說對偶問題,則需要從凸優化問題開始說起。假設我們現在來求解上面的那個凸優化問題的最優解:

觀察上面的最優化問題,便是在一定的約束條件下求解函式的極值,我們上面已經說過拉格朗日乘子法啦,所以這裡便用到了。
使用拉格朗日乘子法針對上面的最優化問題有:

需要明確:其中α≥0、β任意,均為拉格朗日乘子,i=1,2,…,p且j=1,2,…,q
如果按照我們上面談到的拉格朗日乘子法的思路,則應該讓L(x,α,β)對x以及引數α和β進行求導,然後得出結果帶入原始便可求出我們需要的最優解。
但需要注意兩點:
1、這裡引數α和β總共p+q個,如果全部求偏導工作量太大,不現實;
2、並且大家有沒有想過,這個問題可能根本就沒有最優解這種情況存在。
針對上面情況,我們便引出了換一種思路,那就是利用對偶問題,也就是將原問題轉化成其對偶問題進行求解。
下面和大家先說一下對偶問題的基本思想,然後我們再繼續從上面的問題出發,推導其對偶問題,進行求解。
對偶問題的性質:無論原命題的形式如何,對偶問題都是一個凸優化問題,還記得凸優化問題的好處吧,那就是區域性最優解就是全域性最優解,並且容易求解,所以我們將問題轉化為其對偶問題就簡化了問題的求解思路。
上面我們利用拉格朗日乘子法得到了如下式子:

現在我們自定義一個函式如下:

分析上面的自定義函式有:

對上面的式子進行分析:
(1)式說明,當目標函式的約束條件都滿足時,則自定義的函式便是上面需要求解的目標函式f(x) ,(2)則是隻要目標函式的約束條件只有一個不滿足,則自定義的函式便等於無窮大!
所以我們便可以認為自定義的函式θ(x) 是對原理優化問題中的約束條件進行了吸收,是原來的約束優化問題變為無約束優化問題(相對於原來變數x 無約束了),即我們可以將最初的優化問題寫成:

上式便是我們需要優化的原問題
原問題的 對偶問題 便是:

下面我們假設假命題為P,對偶問題為Q!當然對偶問題已經不等價於原問題了,但是二者是存在一定聯絡的,下面我們來講解二者的聯絡,以及如何通過求解對偶問題來得到原問題的最優解!
這裡我們令:


所以有: P>=Q
解釋:大家想一下,函式L中最大值中最小的一個總比最小值中最大的那一個要大,也就是對偶問題提供了原問題最優值的一個下界。
但是大家想,我們是想通過對偶問題求解原問題的最優解,所以只有當二者相等時即P=Q,才可能將原問題轉化成對偶問題進行求解。當然,當滿足一定條件的情況下,便有P=Q。而這個條件便是 slater條件和KTT條件。
slater條件:
slater條件官方正規定義:存在x,使得不等式約束g(x)<=0嚴格成立。
slater條件性質: slater條件是原問題P可以等價於對偶問題Q的一個充分條件,該條件確保了鞍點的存在。
KKT條件:
大家已經知道slater條件已經確保了鞍點的存在,但是鞍點不一定就是最優解啊,所以KKT條件的作用便體現出來了。
KKT條件便是確保鞍點便是原函式最優解的充分條件,當然對於我們前面舉得那個例子,當原問題是凸優化問題時,則KKT條件便是鞍點便是最優解的充要條件。
KKT條件描述為一下三個條件:
1、
2、
3、
解釋:第一個約束條件表明:最優點x必須滿足所有等式及不等式限制條件, 也就是說最優點必須是一個可行解, 這一點自然是毋庸置疑的;
第二個約束條件表明:在最優點x, ∇f必須是∇gi和∇hj的線性組合;
第三個約束條件表明:拉格朗日乘子不等式的一些限制,對於不等式的拉格朗日乘子限制條件有方向性, 所以每一個α都必須大於或等於零, 而等式限制條件沒有方向性,只是β不等於0。
這樣對於slater條件和KKT條件都十分清楚了吧,並且也知道了他們的作用!這樣我們最初的求解凸優化問題便轉化為求解其對偶問題。當前我們的優化目標便是:

因此我們先讓L函式對x求導然後最小化,得出一個優化函式,然後在讓這個優化函式對α,β求導,求出引數α,β!這樣再待會原問題中,便可得到最優解,而下面我們要將的 SMO演算法(序列最小化演算法),正是用於求解引數α,β的!關於SMO演算法數學推導十分複雜,我將在後繼部落格中對於詳細闡述其數學推導過程!!!
文中如有什麼問題,歡迎大家提問和指正!



