2. 程式人生 > >回溯法----旅行售貨員問題java演算法

回溯法----旅行售貨員問題java演算法

阿新 • • 發佈：2019-02-08

我的java演算法：

import java.util.Arrays;

/**
 * Created by Administrator on 2018/4/21.
 */
public class CityTravel {

    static int cityCount = 4;  //城市數量
static int maxstep = cityCount -1;  //城市數量
int shortestval = Integer.MAX_VALUE;    //最小的值
int[] shortestarr = new int[cityCount]; //最小的集合
int stepval = 0;
    int
 
[] steparr = new int[cityCount];
    int[] choosecity = new int[cityCount];

    int[][] citydistanceArr = null;


    public void travel(int step){
        if(step >= maxstep+1){
            //表示走完了所有城市
if(stepval < shortestval){
                shortestarr = Arrays.copyOf(steparr,4);
                shortestval 
 
= stepval;
                System.out.println("當前最短長度是" + shortestval + ",路線是 " + Arrays.toString(shortestarr));
            }
            return;
        }
        //繼續下一步
for(int i = 0; i < cityCount ; i++){
            //下一步沒有走過，並且可達，則選中
if(choosecity[i] == 0 && citydistanceArr[steparr[step-1
 
]][i] != -1){
                steparr[step] = i;
                stepval += citydistanceArr[steparr[step-1]][i];
                choosecity[i] = 1;
                travel(step+1);
                //這裡是退回到上一步
steparr[step] = -1;
                choosecity[i] = 0;
                stepval -= citydistanceArr[steparr[step-1]][i];
            }
        }
    }

    public static void main(String[] args) {
        int[][] citydistanceArr = new int[cityCount][cityCount];
        citydistanceArr[0][0] = -1;
        citydistanceArr[0][1] = 30;
        citydistanceArr[0][2] = 6;
        citydistanceArr[0][3] = 4;

        citydistanceArr[1][0] = 30;
        citydistanceArr[1][1] = -1;
        citydistanceArr[1][2] = 5;
        citydistanceArr[1][3] = 10;

        citydistanceArr[2][0] = 6;
        citydistanceArr[2][1] = 5;
        citydistanceArr[2][2] = -1;
        citydistanceArr[2][3] = 20;

        citydistanceArr[3][0] = 4;
        citydistanceArr[3][1] = 10;
        citydistanceArr[3][2] = 20;
        citydistanceArr[3][3] = -1;

        CityTravel cityTravel = new CityTravel();
        cityTravel.citydistanceArr = citydistanceArr;

        for(int i = 0 ; i < cityCount ; i++){
            cityTravel.steparr[i] = -1;// key表示第幾步,value表示選擇的城市，用於表示當前路線
cityTravel.choosecity[i] = 0;//key表示城市編號,value表示是否選擇，判斷當前路線是否已經存在該城市，用於去重
}

        //城市編號為 0,1,2,3
        //固定第一步走城市0
cityTravel.steparr[0] = 0;//  step的值表示走過的城市編號，表示第0步選擇城市0
cityTravel.choosecity[0] = 1;
        cityTravel.travel(1);

        System.out.println("執行結束================");
        System.out.println(" 最短距離 " + cityTravel.shortestval);
        System.out.println(" 最短路線 " + Arrays.toString(cityTravel.shortestarr));



    }

}

一、問題描述

某售貨員要到若干城市去推銷商品，已知各城市之間的路程(或旅費)。他要選定一條從駐地出發，經過每個城市一次，最後回到駐地的路線，使總的路程(或總旅費)最小。

        如下圖：1，2，3，4 四個城市及其路線費用圖，任意兩個城市之間不一定都有路可達。

       

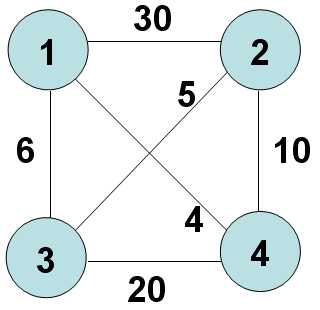
二、問題理解

      1.分支限界法利用的是廣度優先搜尋和最優值策略。

      2.利用二維陣列儲存圖資訊City_Graph[MAX_SIZE][MAX_SIZE]

         其中City_Graph[i][j]的值代表的是城市i與城市j之間的路徑費用

         一旦一個城市沒有通向另外城市的路，則不可能有迴路，不用再找下去了

      3. 我們任意選擇一個城市，作為出發點。（因為最後都是一個迴路，無所謂從哪出發）

      下面是關鍵思路：

       想象一下，我們就是旅行員，假定從城市1出發，根據廣度優先搜尋的思路，我們要把從城市1能到達的下一個城市，都要作為一種路徑走一下試試。

       可是程式裡面怎麼實現這種“試試”呢？

       利用一種資料結構，儲存我們每走一步後，當前的一些狀態引數，如，我們已經走過的城市數目（這樣就知道，我們有沒有走完，比如上圖，當我們走了四個城市之後，無論從第四個城市是否能回到起點城市，都就意味著我們走完了，只是這條路徑合不合約束以及能不能得到最優解的問題）。這裡把，這種資料結構成為結點。這就需要另一個數據結構，儲存我們每次試出來的路徑，這就是堆。

       資料結構定義如下：

  1. Node{  
  2.    int s;           //結點深度，即當前走過了幾個城市
  3.    int x[MAX_SIZE]; //儲存走到這個結點時的路徑資訊
  4. }  
  5. MiniHeap{  
  6.    //儲存所有結點並提供一些結點的操作
  7. }  
 

       a.我們剛開始的時候不知道最總能得到的路徑是什麼，所以我們，就認為按照城市編號的次序走一遍。於是有了第一個結點0，放入堆             中。 相當於來到了城市1(可以是所有城市中的任意一個，這裡姑且設為圖中城市1)。

       b.從城市1，出發，發現有三條路可走，分別走一下，這樣就產生了三個結點，都放入堆中。

          結點1 資料為：x[1 2 3 4]，深度為s=1（深度為0表示在城市1還沒有開始走），這說明，結點1是從城市1走來，走過了1個城                                      市，當前停在城市2，後面的城市3 和城市4都還沒有走，但是具體是不是就按照3.4的順序走，這個不一定。

          結點2 資料為：x[1 3 2 4]，深度為s=1，表示，從城市1走來，走過了1個城市，當前停在了城市3，後面2.4城市還沒走

          結點3 資料為：x[1 4 3 2]，深度為s=1，表示，從城市1走來，走過了1個城市，當前停在了城市4，後面3.2城市還沒有走

       c. 從堆中取一個結點，看看這個結點是不是走完了的，也就是要看看它的深度是不是3，是的話，說明走完了，看看是不是能回到起                點，如果可以而且費用少於先前得到最優的費用，就把當前的解作為最優解。

           如果沒有走完，就繼續把這條路走下去。

以上就是簡單的想法，而實際的程式中，堆還需要提供對結點的優先權排序的支援。而當前結點在往下一個城市走時，也是需要約束和限界函式，這些書上講的很清楚，不懂，就翻翻書。

有點要提出來說說的就是結點優先權和限界函式時都用到了一個最小出邊和，就相當於把所有城市最便宜的一條路（邊）費用加起來的值。

下面是程式碼

  1. #include <stdio.h>
  2. #include <istream>
  3. usingnamespace std;  
  4. //---------------------巨集定義------------------------------------------
  5. #define MAX_CITY_NUMBER 10          //城市最大數目
  6. #define MAX_COST 10000000           //兩個城市之間費用的最大值
  7. //---------------------全域性變數----------------------------------------
  8. int City_Graph[MAX_CITY_NUMBER][MAX_CITY_NUMBER];  
  9.                             //表示城市間邊權重的陣列
  10. int City_Size;              //表示實際輸入的城市數目
  11. int Best_Cost;              //最小費用
  12. int Best_Cost_Path[MAX_CITY_NUMBER];  
  13.                             //最小費用時的路徑  
  14. //------------------------定義結點---------------------------------------
  15. typedef struct Node{  
  16.     int lcost;              //優先順序
  17.     int cc;                 //當前費用
  18.     int rcost;              //剩餘所有結點的最小出邊費用的和
  19.     int s;                  //當前結點的深度，也就是它在解陣列中的索引位置
  20.     int x[MAX_CITY_NUMBER]; //當前結點對應的路徑
  21.     struct Node* pNext;     //指向下一個結點
  22. }Node;  
  23. //---------------------定義堆和相關對操作--------------------------------
  24. typedef struct MiniHeap{  
  25.     Node* pHead;             //堆的頭
  26. }MiniHeap;  
  27. //初始化
  28. void InitMiniHeap(MiniHeap* pMiniHeap){  
  29.     pMiniHeap->pHead = new Node;  
  30.     pMiniHeap->pHead->pNext = NULL;  
  31. }  
  32. //入堆
  33. void put(MiniHeap* pMiniHeap,Node node){  
  34.     Node* next;  
  35.     Node* pre;   
  36.     Node* pinnode = new Node;         //將傳進來的結點資訊copy一份儲存
  37.                                       //這樣在函式外部對node的修改就不會影響到堆了
  38.     pinnode->cc = node.cc;  
  39.     pinnode->lcost = node.lcost;  
  40.     pinnode->pNext = node.pNext;  
  41.     pinnode->rcost = node.rcost;  
  42.     pinnode->s = node.s;  
  43.     pinnode->pNext = NULL;  
  44.     for(int k=0;k<City_Size;k++){  
  45.         pinnode->x[k] = node.x[k];  
  46.     }  
  47.     pre = pMiniHeap->pHead;  
  48.     next = pMiniHeap->pHead->pNext;  
  49.     if(next == NULL){  
  50.         pMiniHeap->pHead->pNext = pinnode;  
  51.     }  
  52.     else{  
  53.         while(next != NULL){  
  54.             if((next->lcost) > (pinnode->lcost)){ //發現一個優先順序大的，則置於其前面
  55.                 pinnode->pNext = pre->pNext;  
  56.                 pre->pNext = pinnode;  
  57.                 break;                            //跳出

  58. 相關推薦

    演算法java實現--回溯法--旅行售貨員問題--排列樹

    旅行售貨員問題的java實現（回溯法--排列樹） 具體問題描述以及C/C++實現參見網址 http://blog.csdn.net/liufeng_king/article/details/8890603 /** * 旅行售貨員問題--回溯法 * @author

    回溯法----旅行售貨員問題java演算法

    我的java演算法： import java.util.Arrays; /** * Created by Administrator on 2018/4/21. */ public class CityTravel { static int ci

    回溯法----旅行售貨員問題

    一、問題 二、程式碼實現        程式實現了 遞歸回溯 解決該問題        迭代回溯演算法仍在考慮中... /**************************************************************** *問 題：旅行

    回溯法-旅行售貨員問題(C語言)

    1、旅行員售貨問題 問題描述 某售貨員要到若干城市去推銷商品，已知各城市之間的路程（旅費），他要選定一條從駐地出發，經過每個城市一遍，最後回到駐地的路線，使總的路程（總旅費）最小。(必須從1號店出發,最後回到出發地) #include <stdio.h>

    分支限界法-旅行售貨員問題

    旅行售貨員問題的解空間樹是一顆排序樹。與前面關於子集樹的討論類似，實現對排列樹搜尋的優先佇列式分支限界法也可以用兩種不同的實現方式。一種是僅使用一個優先佇列來儲存活結點。優先佇列中的每個活結點都儲存從根到該活結點的相應路徑。另一種是用優先佇列來儲存活結點，並同時儲存當前已構造出的部分排列樹。在這

    分支限界法---旅行售貨員問題

    1 N: int = 4 2 MAX_WEIGHT: int = 4000 3 NO_PATH: int = -1 4 City_Graph = [[int('0')] * (N+1) for _ in range(N+1)] # 初始化dp 5 x = [int('0') * (N+1)

    回溯法—裝載問題—java實現

    問題描述：一共有n個貨物要裝上兩艘重量分別為c1和c2的輪船上，其中貨物i的重量為Wi，且：                                  要求確定是否有一個合理的裝載方案可將貨物裝上這兩艘輪船。採取策略：        (1)首先將第一艘輪船儘可能裝滿；

    【資料結構與演算法】回溯法解決N皇后問題，java程式碼實現

    N皇后問題 問題描述 在8×8格的國際象棋上擺放八個皇后，使其不能互相攻擊，即任意兩個皇后都不能處於同一行、同一列或同一斜線上，問有多少種擺法，這稱為八皇后問題。 延伸一下，便為N皇后問題。 核心思想 解決N皇后問題有兩個關鍵點。一是如何進行放置棋子，二是如何驗證棋子是否符合

    數獨求解演算法（回溯法和唯一解法）java實現

    數獨（すうどく，Sudoku）是一種運用紙、筆進行演算的邏輯遊戲。玩家需要根據9×9盤面上的已知數字，推理出所有剩餘空格的數字，並滿足每一行、每一列、每一個粗線宮內的數字均含1-9，不重複。     注：數獨的各種知識和解決思路請 參考http://www.llang

    旅行售貨員問題（回溯法搜尋排列樹）

    {        if (node.firstchild ==null)//到了葉結點...{                        return (int)((ArrayList)g.AdjacentMatrix[node.data])[0];//葉結點與根結點之間的路徑，因為需要回路       

    旅行售貨員問題-回溯法-深度搜索

    問題描述:某售貨員要到若干城市去推銷商品，已知各城市之間的路程，他要選定一條從駐地出發，經過每個城市一遍，最後回到住地的路線，使總的路程最短。演算法描述：回溯法，序列樹， 假設起點為 1。演算法開始時 x = [1, 2, 3, ..., n]x[1 : n]有兩重含義 x[

    旅行售貨員問題 回溯法 與 01揹包的區別

    #include<stdio.h>//01揹包回溯法是拿一個少一個，順序無關，屬於子集樹 #include<string.h>//售貨員問題是與順序有關，屬於排列樹，用一個標誌陣列標誌就可以 #define MAX_INT 1000; int mg[

    旅行售貨商問題 -- 回溯法

    temp fine tput 初始 clu += put true lse /*旅行售貨員問題回溯法*/ #include<stdio.h> #define N 4 int cc,//當前路徑費用 bestc;//當前最優解費用 i

    遞迴、回溯-旅行售貨員問題

    某售貨員到若干城市去推銷商品，已知各城市之間的路程(或旅費)。他要選定一條路線，經過每個城市一遍最後回到駐地的路線，使得總的路程(或總旅費)最小（預設從1號城市開始）。 輸入：城市的數目n，城市a，b，以及其之間的路程d。 輸出：最短的路程，最短的路徑方案。 執行結果：

    Leetcode——回溯法常考演算法整理

    Leetcode——回溯法常考演算法整理 Preface Leetcode——回溯法常考演算法整理 Definition Why & When to Use Backtrakcing How to Use Bac

    演算法題（二十一）：回溯法解決矩陣路徑問題

    題目描述 請設計一個函式，用來判斷在一個矩陣中是否存在一條包含某字串所有字元的路徑。路徑可以從矩陣中的任意一個格子開始，每一步可以在矩陣中向左，向右，向上，向下移動一個格子。如果一條路徑經過了矩陣中的某一個格子，則之後不能再次進入這個格子。 例如 a b c e s f c s a d e

    回溯法演算法實驗

    桂 林 理 工 大 學 實  驗  報  告 班級  軟體工程16-1班  學號  3162052051116  姓名  張識虔  同組實驗者      

    【資料結構與演算法】回溯法解決裝載問題

    回溯法解決裝載問題(約束函式優化) 解題思想 遍歷各元素，若cw+w[t]<=c(即船可以裝下)，則進入左子樹，w[t]標記為1，再進行遞迴，若cw+r>bestw(即當前節點的右子樹包含最優解的可能),則進入右子樹，否則，則不遍歷右子樹。 完整程式碼實現如下 p

    小朋友學經典演算法（14）：回溯法和八皇后問題

    一、回溯法 回溯法（探索與回溯法）是一種選優搜尋法，又稱為試探法，按選優條件向前搜尋，以達到目標。但當探索到某一步時，發現原先選擇並不優或達不到目標，就退回一步重新選擇，這種走不通就退回再走的技術為回溯法，而滿足回溯條件的某個狀態的點稱為“回溯點”。 二、八皇后問題 （一）問

    【基礎演算法】回溯法與八皇后問題

    #include"iostream" #include"stdlib.h" using namespace std; int x[8],tot=0; bool B(int x[],int k) { int i; for(i=0;i<k;i++) if(x[i]==x[