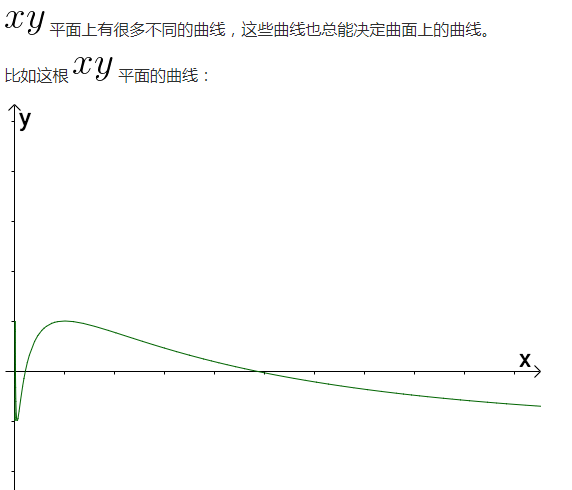
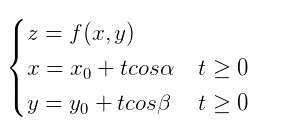什麼是全導數、偏導數、方向導數?
阿新 • • 發佈:2019-02-09
全導數是多元函式中的一個概念。
我們知道一元函式的情況下,導數就是函式的變化率,從幾何意義上看就是:
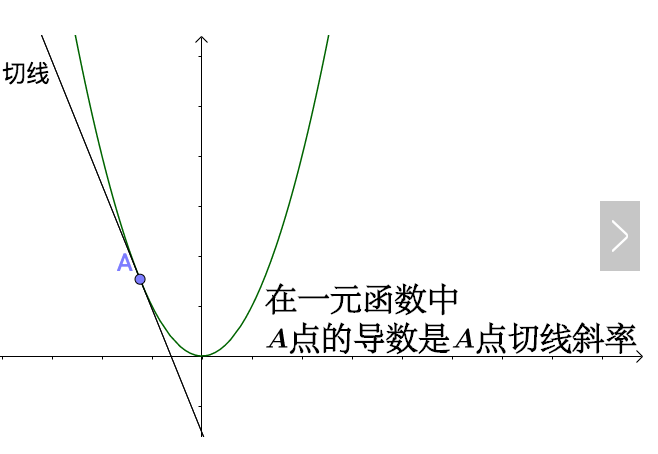
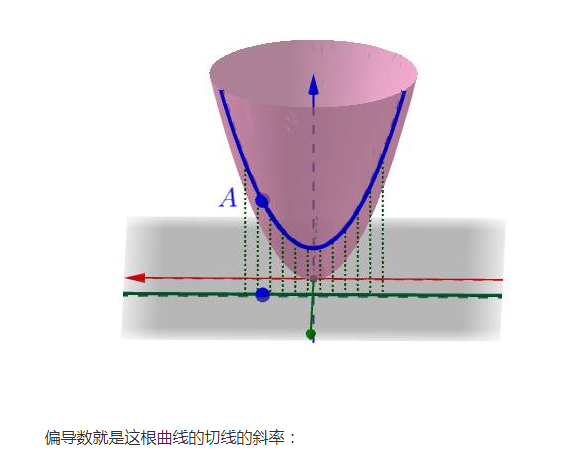
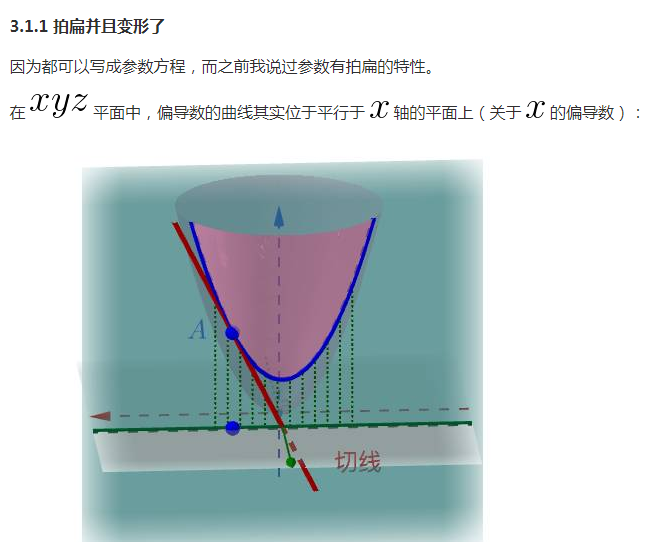
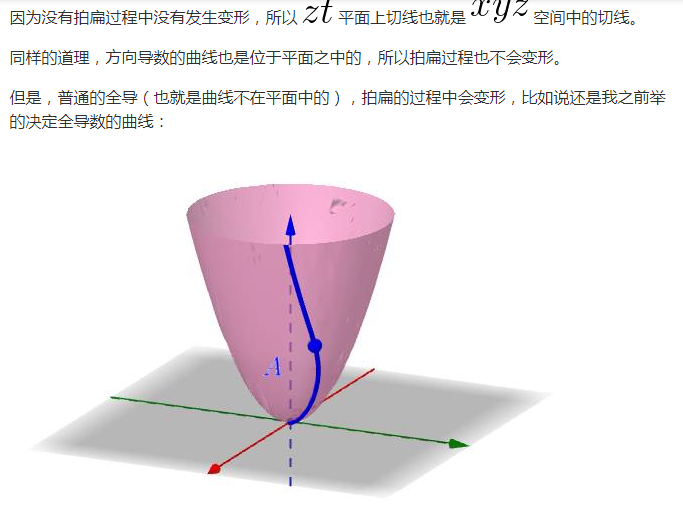
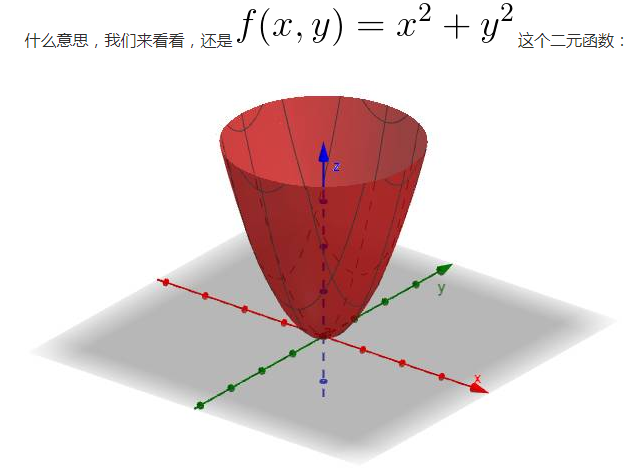
但是在多元的情況下比一元的複雜,下面我用二元函式來舉例子(三元我也畫不出來),比如這樣一個曲面上的一點 ![]() :
:
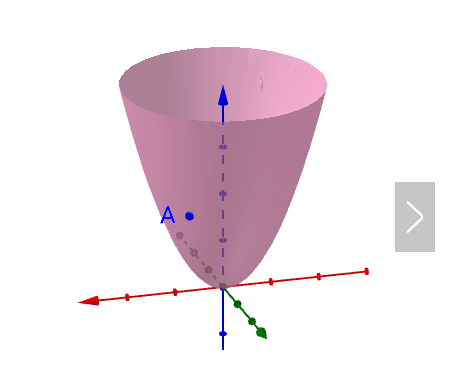
在曲面上可以做無數條過 ![]() 點的曲線(圖上隨便畫了三根):
點的曲線(圖上隨便畫了三根):
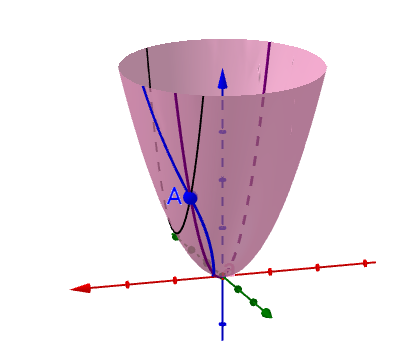
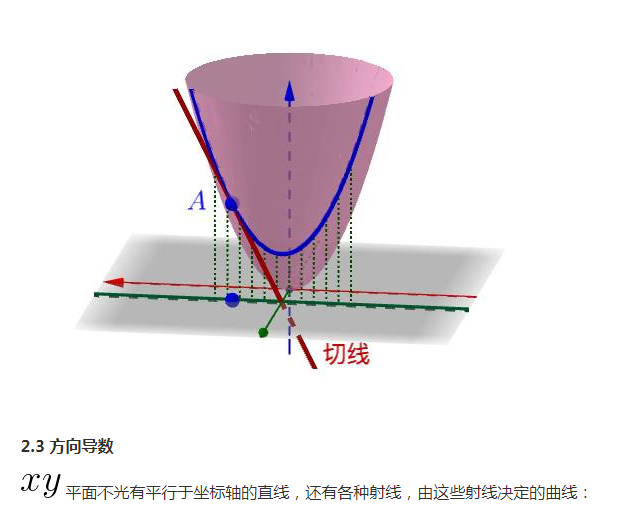
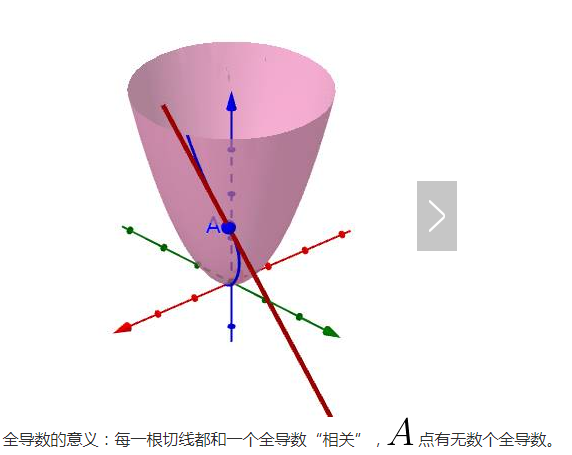
每根曲線都可能可以(也有作不出來的情況,你想想一元的時候也有作不出切線的情況)作一根切線,比如(隨便挑了一根切線來畫,都畫出來太亂了):
最精簡的回答已經完了,後面我就要講一些細節了,主要闡述下面兩個細節:
-
方向導數、偏導數是特殊的全導數
-
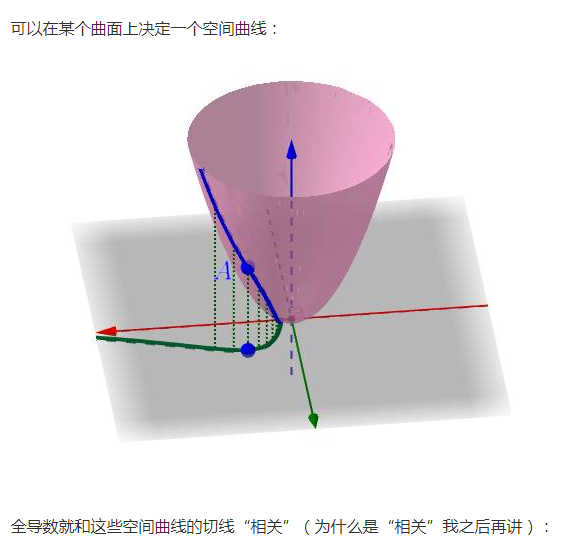
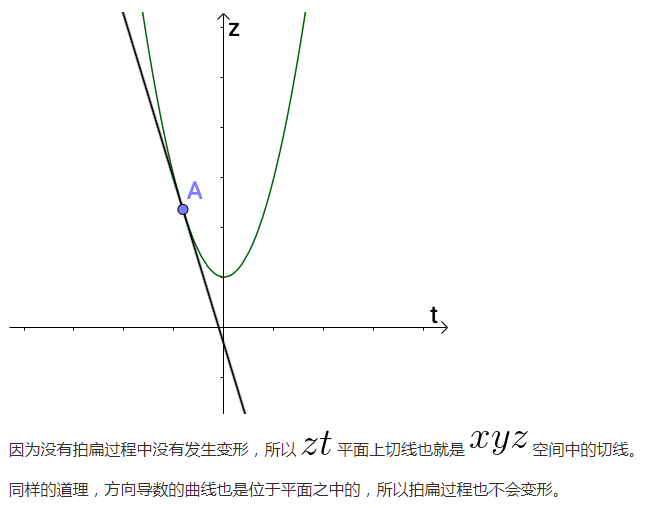
每一根切線都和一個全導數“相關”,這個“相關”是什麼意思?難道不就是切線的斜率就是全導數嗎?
順便說一下,如果所有這些切線共面的話,那麼這個平面就是切平面(全微分),可以參考我之前的回答如何直觀理解全微分?。
1 引數方程
為了繼續講下去,我們需要了解下所需要的技術手段:引數方程。
引數方程的用處很多,下面講解下我們需要了解的部分。
1.1 通過引數方程來描述所有的曲線
要描述所有這些曲線,我們就需要一些數學手段,這就是引數方程。
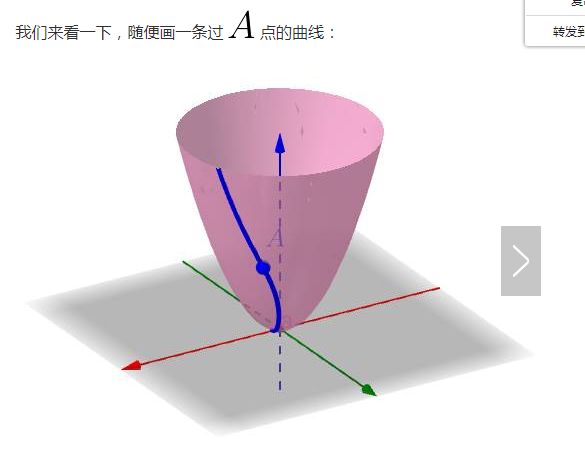
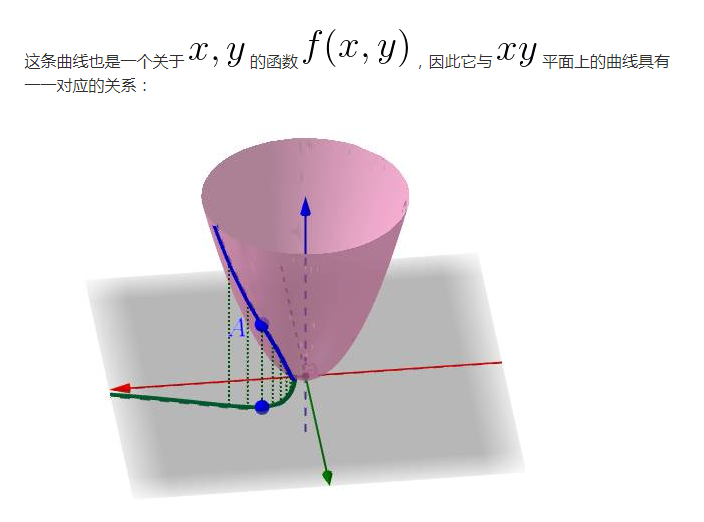
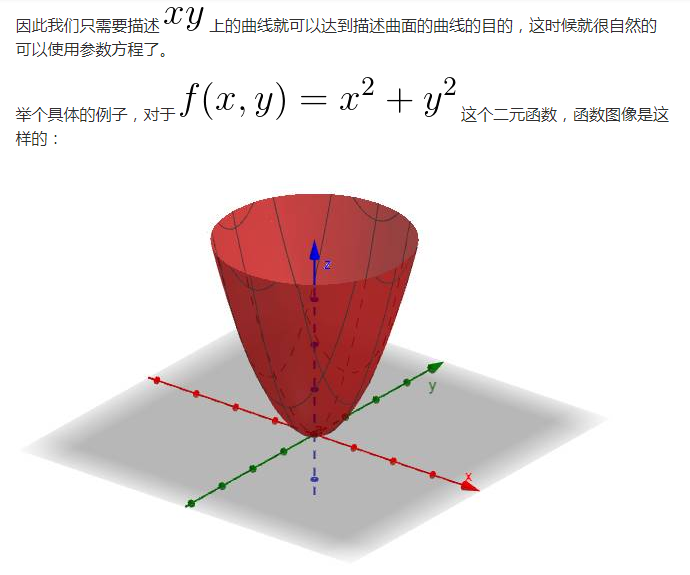
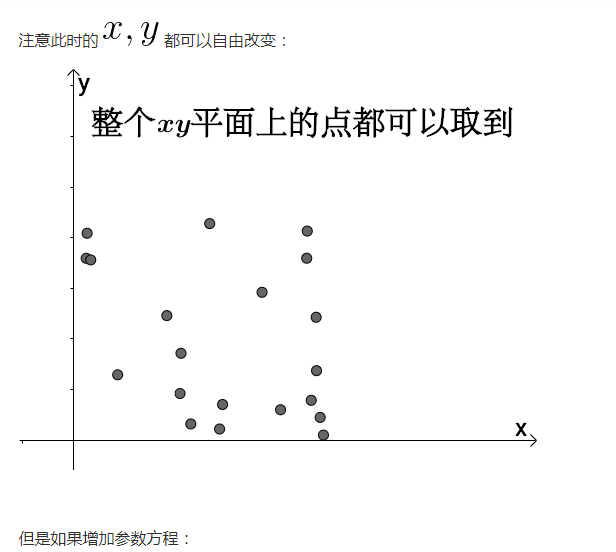
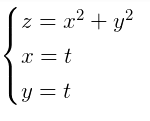
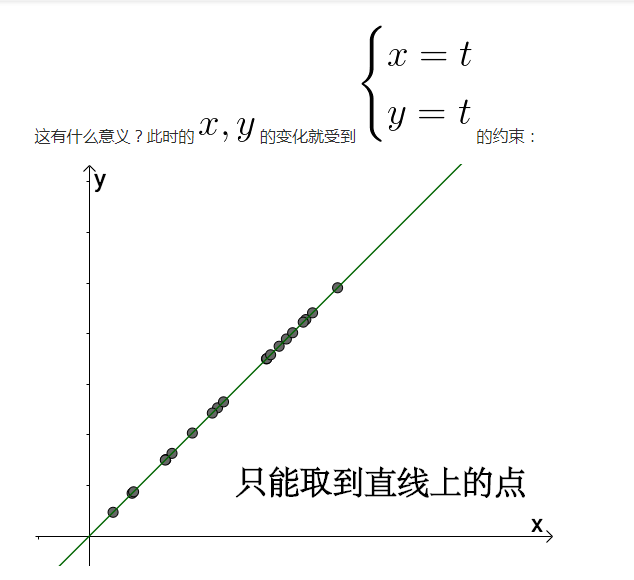
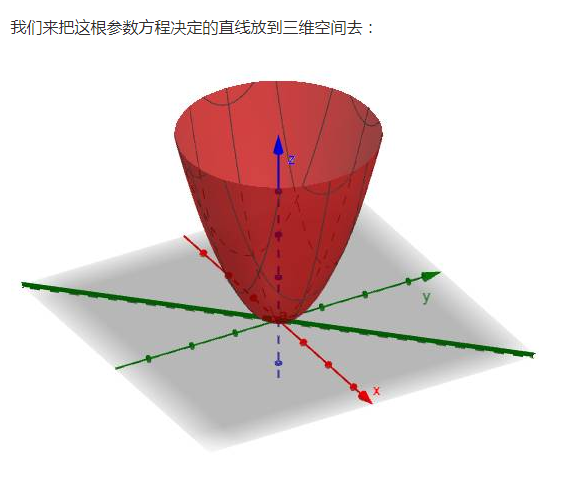
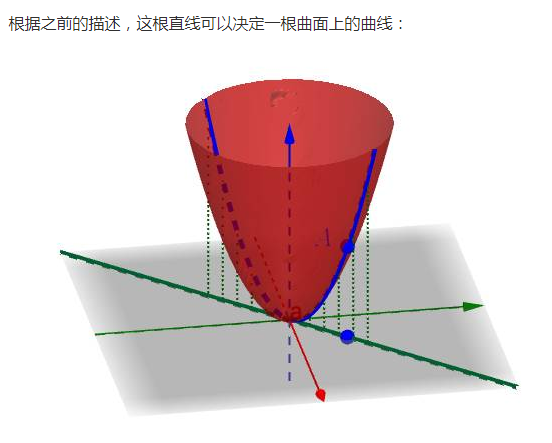
這根曲面上的曲線就是剛才說過的:
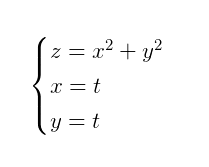
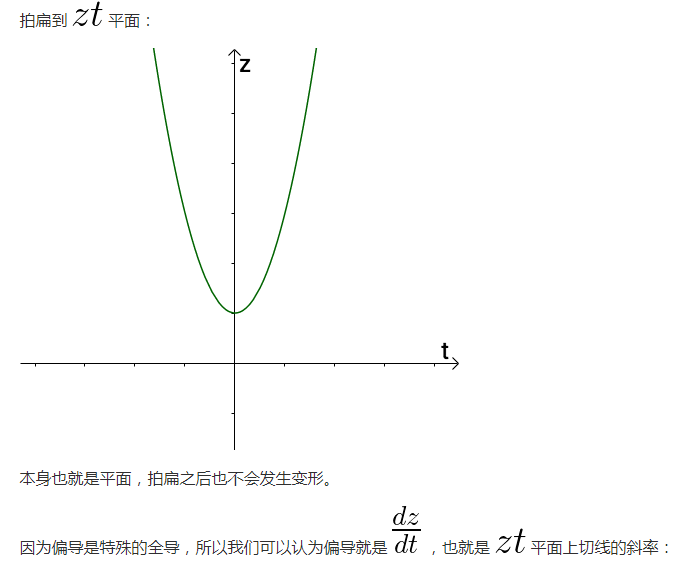
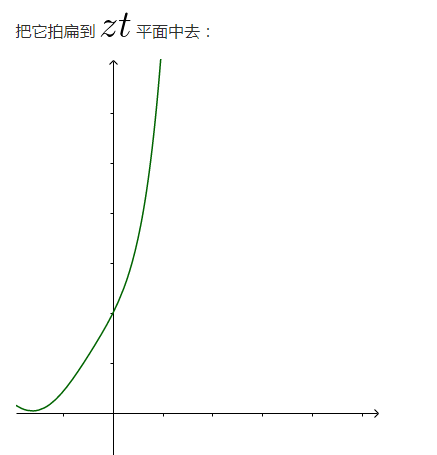
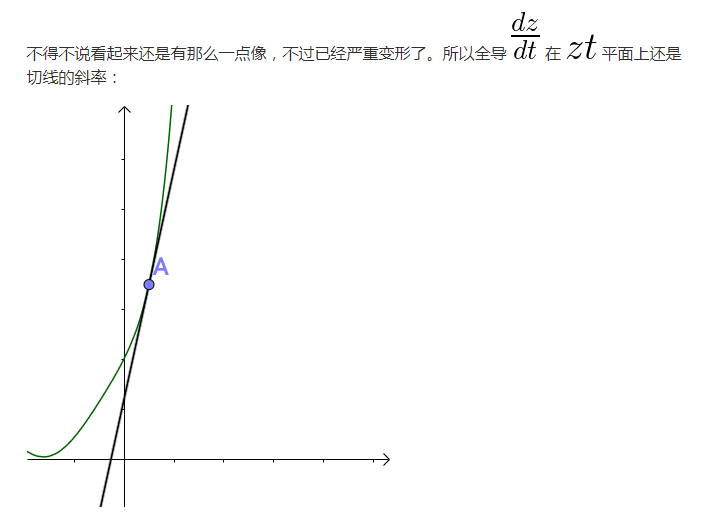
1.2 引數方程可以拍扁三維影象
從另外一個角度看,引數方程可以把三維的影象一巴掌拍扁:

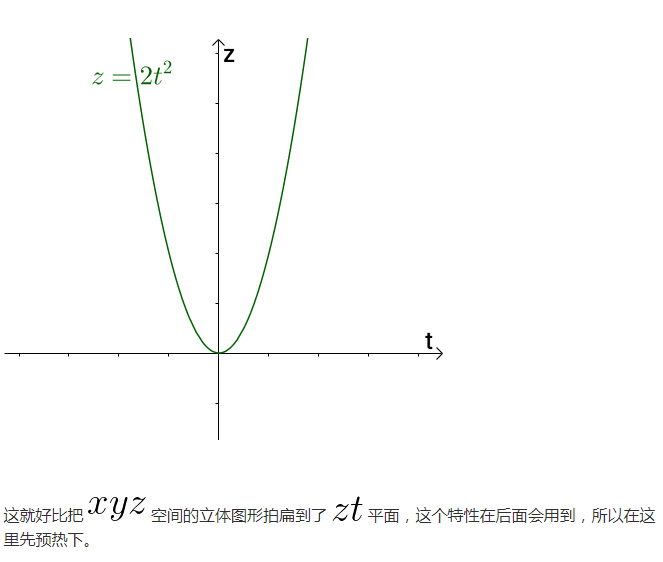
2 全導數、偏導數、方向導數
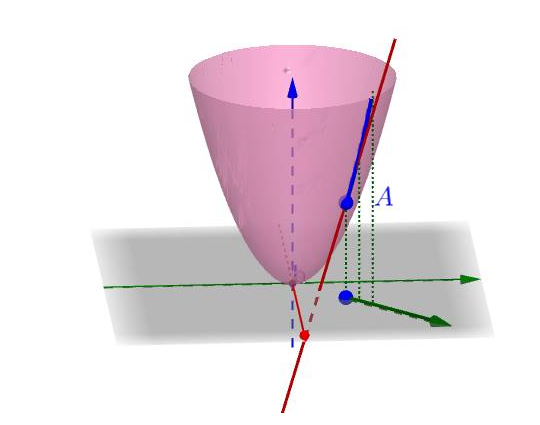
講完“所有曲線”之後,我們要來講這些曲線的切線了,不同的曲線有不同的切線,也就有不同型別的導數。
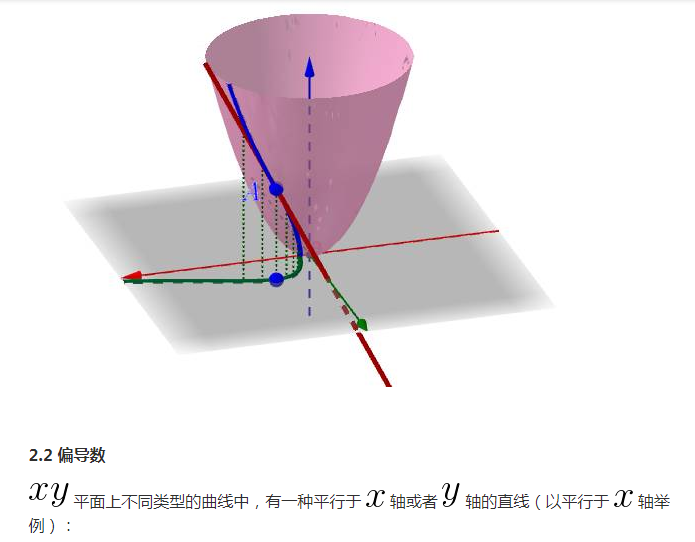
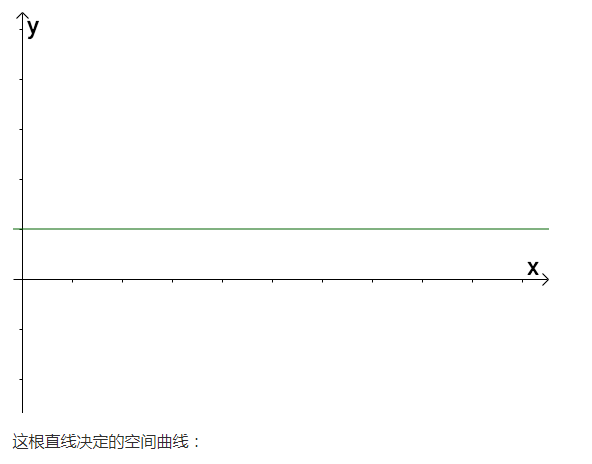
2.1 全導數