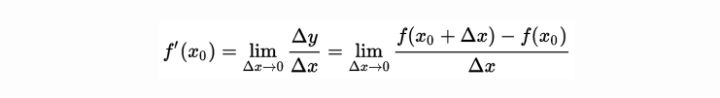導數、偏導數、梯度
一、導數(derivative)
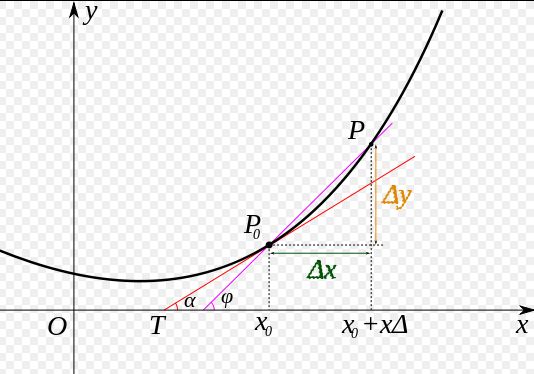
導數,是我們最早接觸的一元函數中定義的,可以在 xy 平面直角坐標系中方便的觀察。當 Δx→0時,P0處的導數就是因變量y在x0處的變化率,反映因變量隨自變量變化的快慢;從幾何意義來講,函數在一點的導數值就是過這一點切線的斜率。
二、偏導數(partial derivative)
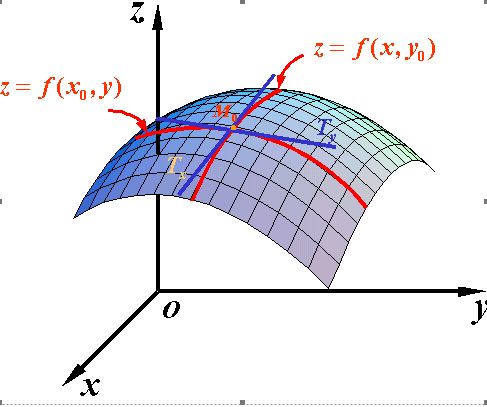
偏導數對應多元函數的情況,對於一個 n元函數 y=f(x1,x2,…,xn),在 ?n 空間內的直角坐標系中,函數沿著某一條坐標軸方向的導數,就是偏導數。在某一點處,求 xi軸方向的導數,就是將其他維的數值看做常數,去截取一條曲線出來,這條曲線的導數可以用上面的導數定義求。求出來就是此點在這條軸方向上的偏導數。
三、方向導數 (directional derivative)
很多時候,僅僅有了坐標軸方向上的偏導數是不夠的,我們還想知道任意方向上的導數。函數在任意方向上的導數就是方向導數。而空間中任意方向,是一定可以用坐標軸線性組合來表示的,這就架起了偏導數和方向導數的橋梁:
令 ,
其中,α是由偏導數定義的向量A 與 我們自己找的單位方向向量 I之間的夾角。
現在我們來討論函數![]() 在一點
在一點![]() 沿某一方向的變化率問題.
沿某一方向的變化率問題.
定義 設函數![]() 在點
在點![]()
![]() 的某一鄰域
的某一鄰域![]() 內有定義.自點
內有定義.自點![]() 引射線
引射線![]() .設
.設![]() 軸正向到射線
軸正向到射線![]() 的轉角為
的轉角為![]() (逆時針方向:
(逆時針方向:![]()
![]() 0;順時針方向:
0;順時針方向:![]()
![]() 0),並設
0),並設![]() '(
'(![]() +△
+△![]() ,
,![]() +△
+△![]() )為
)為![]() 上的另一點且
上的另一點且![]() '∈
'∈![]() .我們考慮函數的增量
.我們考慮函數的增量![]()
![]() (1)
(1)
從定義可知,當函數![]()
![]() 在點
在點![]()
![]() 的偏導數
的偏導數![]() x、
x、![]() y存在時,函數在點
y存在時,函數在點![]() 沿著
沿著![]() 軸正向
軸正向![]()
![]() =
=![]() ,
,![]() 軸正向
軸正向![]() =
=![]() 的方向導數存在且其值依次為
的方向導數存在且其值依次為![]() x、
x、![]() y,函數
y,函數![]()
![]() 在點
在點![]() 沿
沿![]() 軸負向
軸負向![]() =
=![]() ,
,![]() 軸負向
軸負向![]() =
=![]() 的方向導數也存在且其值依次為-
的方向導數也存在且其值依次為-![]() x、-
x、-![]() y.
y.
關於方向導數![]() 的存在及計算,我們有下面的定理.
的存在及計算,我們有下面的定理.
定理 如果函數![]() 在點
在點![]()
![]() 是可微分的,那末函數在該點沿任一方向的方向導數都存在,且有
是可微分的,那末函數在該點沿任一方向的方向導數都存在,且有
![]()
![]() (2)
(2)
其中![]() 為
為![]() 軸到方向
軸到方向![]() 的轉角.
的轉角.
證 根據函數![]() 在點
在點![]()
![]() 可微分的假定,函數的增量可以表達為
可微分的假定,函數的增量可以表達為
![]()
兩邊各除以![]() ,得到
,得到
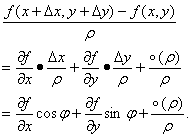
所以 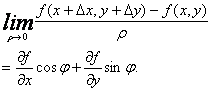
![]() 這就證明了方向導數存在且其值為
這就證明了方向導數存在且其值為
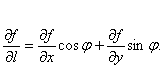
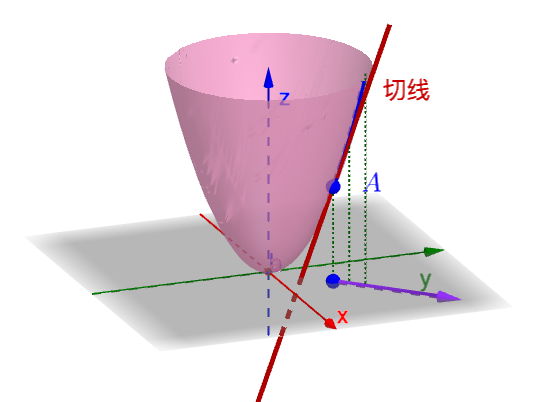
在訓練神經網絡時,我們都是通過定義一個代價函數(cost function),然後通過反向傳播更新參數來最小化代價函數,深度神經網絡可能有大量參數,因此代價函數是一個多元函數,多元函數與一元函數的一個不同點在於,過多元函數的一點,可能有無數個方向都會使函數減小。引申到數學上,我們可以把山這樣的曲面看作一個二元函數z=f(x,y),二元函數是多元函數裏最簡單的情形,也是易於可視化直觀理解的。前面提到一元函數導數的幾何意義是切線的斜率,對於二元函數,曲面上的某一點(x0,y0,z0)會有一個切平面,切平面上的無數條直線都是過這一點的切線,這些切線的斜率實際上就是過這一點的無數個方向導數的值,和一元函數一樣,方向導數的值實際反映了多元函數在這一點沿某個方向的變化率。
四、梯度 (gradient)與神經網絡中的梯度下降
在上面的方向導數中,
- A是固定的
- |I|=1是固定的
- 唯一變化的就是 α
當 I與 A 同向的時候,方向導數取得最大,此時我們定義一個向量 ,其方向就是 A的方向,大小就是 A的模長,我們稱這個向量就是此點的梯度。沿著梯度方向,就是函數增長最快的方向,那麽逆著梯度方向,自然就是函數下降最快的方向。由此,我們可以構建基於梯度的優化算法。正如下山必然有一條最陡峭、最快的路徑,方向導數也有一個最小值,在最小值對應的方向上,函數下降最快,而這個方向其實就是梯度的反方向。對於神經網絡,在方向導數最小的方向更新參數可以使代價函數減小最快,因此梯度下降法也叫最速下降法。
向量(fx(x0,y0),fy(x0,y0))就是函數f(x,y)在點P0(x0,y0)的梯度,由此引出梯度的概念,梯度就是一個向量,這個向量的每個元素分別是多元函數關於每個自變量的偏導數。方向導數的值最大,多元函數增加最快,也就是說梯度的方向就是函數增加最快的方向,方向導數的值最小,多元函數減小最快,也就是在梯度相反的方向上,方向導數最小。
1.梯度的定義
與方向導數有關聯的一個概念是函數的梯度.
定義 設函數![]() 在平面區域
在平面區域![]() 內具有一階連續偏導數,則對於每一點
內具有一階連續偏導數,則對於每一點![]()
![]()
![]() ,都可定出一個向量
,都可定出一個向量
![]()
這向量稱為函數![]() =
=![]() 在點
在點![]()
![]() 的梯度,記作
的梯度,記作![]()
![]()
![]() ,即
,即
![]()
![]()
![]() =
= ![]()
如果設![]() 是與方向
是與方向![]() 同方向的單位向量,則由方向導數的計算公式可知
同方向的單位向量,則由方向導數的計算公式可知
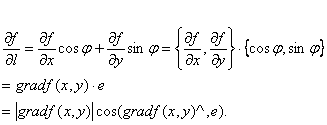
這裏,(![]()
![]()
![]() ^,e)表示向量
^,e)表示向量![]()
![]()
![]() 與
與![]() 的夾角.由此可以看出,就是梯度在射線
的夾角.由此可以看出,就是梯度在射線![]() 上的投影,當方向
上的投影,當方向![]() 與梯度的方向一致時,有
與梯度的方向一致時,有
![]() (
(![]()
![]()
![]() ^,
^,![]() )
) ![]() 1,
1,
從而![]() 有最大值.所以沿梯度方向的方向導數達到最大值,也就是說,梯度的方向是函數
有最大值.所以沿梯度方向的方向導數達到最大值,也就是說,梯度的方向是函數![]()
![]() 在這點增長最快的方向.因此,我們可以得到如下結論:
在這點增長最快的方向.因此,我們可以得到如下結論:
函數在某點的梯度是這樣一個向量,它的方向與取得最大方向導數的方向一致,而它的模為方向導數的最大值.
由梯度的定義可知,梯度的模為
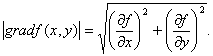
當![]() 不為零時,那麽
不為零時,那麽![]() 軸到梯度的轉角的正切為
軸到梯度的轉角的正切為
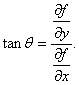
我們知道,一般說來二元函數![]() 在幾何上表示一個曲面,這曲面被平面z=c(c是常數)所截得的曲線
在幾何上表示一個曲面,這曲面被平面z=c(c是常數)所截得的曲線![]() 的方程為
的方程為
![]()
這條曲線![]() 在
在![]() 面上的投影是一條平面曲線
面上的投影是一條平面曲線![]() (圖8―10),它在
(圖8―10),它在![]() 平面直角坐標系中的方程為
平面直角坐標系中的方程為
![]()
對於曲線![]() 上的一切點,已給函數的函數值都是
上的一切點,已給函數的函數值都是![]() ,所以我們稱平面曲線
,所以我們稱平面曲線![]() 為函數
為函數![]() 的等高線.
的等高線.
由於等高線![]() 上任一點
上任一點![]() 處的法線的斜率為
處的法線的斜率為
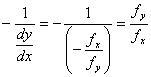 ,
,
所以梯度 ![]()
為等高線上點![]() 處的法向量,因此我們可得到梯度與等高線的下述關系:函數
處的法向量,因此我們可得到梯度與等高線的下述關系:函數![]() 在點
在點![]()
![]() 的梯度的方向與過點
的梯度的方向與過點![]() 的等高線
的等高線![]() 在這點的法線的一個方向相同,且從數值較低的等高線指向數值較高的等高線(圖8―10),而梯度的模等於函數在這個法線方向的方向導數.這個法線方向就是方向導數取得最大值的方向.
在這點的法線的一個方向相同,且從數值較低的等高線指向數值較高的等高線(圖8―10),而梯度的模等於函數在這個法線方向的方向導數.這個法線方向就是方向導數取得最大值的方向.
2、解釋方向導數只有一個最小值:

具有一階連續偏導數,意味著可微。可微意味著函數 在各個方向的切線都在同一個平面上,也就是切平面。所有的切線都在一個平面上,就好像光滑的筆直的玻璃上,某一點一定有且只有一個最陡峭的地方,因為方向導數是切線的斜率,方向導數最大也就意味著最陡峭。
原文鏈接 https://blog.csdn.net/loveliuzz/article/details/83543016
個人理解:
1、導數,函數沿某個分量的變化率,對於一維來說,只有一個分量,故沒有偏導數、方向導數的概念,或者說,導數,偏導數,方向導數等價
2、導數、偏導數、方向導數 都是一個數值,為標量,表征變化率
3、對於多元函數,生活在多維空間,在各個方向都有變化率,這些變化率是方向導數,各個方向變化率可能不一樣
4、基向量方向的方向導數 是 偏導數,故偏導數是特殊的方向導數
5、各個方向導數中,最大的方向導數稱作梯度,其方向為梯度方向
6、方向導數可以由偏導數算出 比如(cos(a),sin(a))這個方向的導數 等於 fx(x,y)cos(a)+fy(x,y)sin(a)
7、方向導數 等於 (fx(x,y),fy(x,y)) * (cos(a),sin(a)),可知二者共線最大,則梯度方向為 (fx(x,y),fy(x,y))
導數、偏導數、梯度