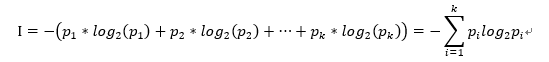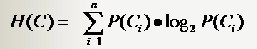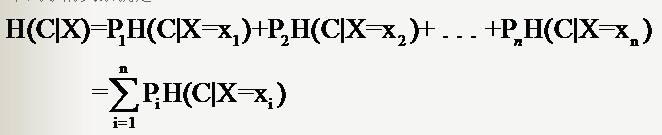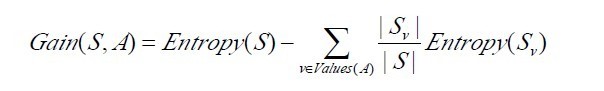一、決策樹基本概念及演算法優缺點

1.什麼是決策樹

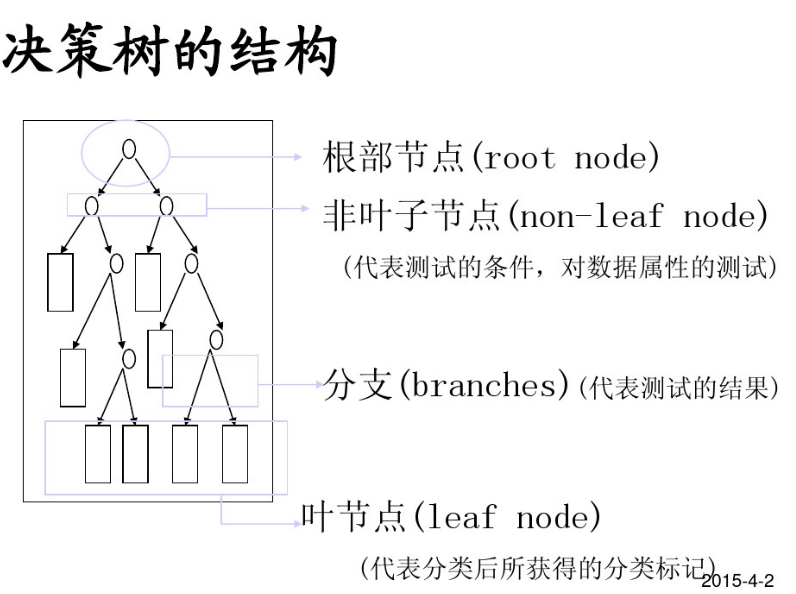
分類決策樹模型是一種描述對例項進行分類的樹形結構。決策樹由結點和有向邊組成。結點有兩種型別：內部結點和葉結點。內部結點表示一個特徵或屬性，葉結點表示一個類。
決策樹（Decision Tree），又稱判定樹，是一種以樹結構（包括二叉樹和多叉樹）形式來表達的預測分析模型。

• 通過把例項從根節點排列到某個葉子節點來分類例項
• 葉子節點即為例項所屬的分類
• 樹上每個節點說明了對例項的某個屬性的測試，節點的每個後繼分支對應於該屬性的一個可能值

2 決策樹結構

3 決策樹種類

分類樹—對離散變數做決策樹
迴歸樹—對連續變數做決策樹

4 決策樹演算法

• 有監督的學習
• 非引數學習演算法
• 自頂向下遞迴方式構造決策樹
• 在每一步選擇中都採取在當前狀態下最好/優的選擇
  決策樹學習的演算法通常是一個遞迴地選擇最優特徵，並根據該特徵對訓練資料進行分割，使得各
  個子資料集有一個最好的分類的過程。在決策樹演算法中，ID3基於資訊增益作為屬性選擇的度量，C4.5基於資訊增益比作為屬性選擇的度量，CART基於基尼指數作為屬性選擇的度量。

5 決策樹學習過程

• 特徵選擇
• 決策樹生成：遞迴結構，對應於模型的區域性最優
• 決策樹剪枝：縮小樹結構規模、緩解過擬合，對應於模型的全域性選擇

6 決策樹優缺點

優點：
(1) 速度快：

計算量相對較小，且容易轉化成分類規則。只要沿著樹根向下一直走到葉，沿途的分裂條件就能夠唯一確定一條分類的謂詞。
(2) 準確性高：挖掘出的分類規則準確性高，便於理解，決策樹可以清晰的顯示哪些欄位比較重要，即可以生成可以理解的規則。
(3)可以處理連續和種類欄位
缺點：
(1) 對於各類別樣本數量不一致的資料，資訊增益偏向於哪些具有更多數值的特徵
(2) 易於過擬合
(3) 對連續的欄位比較難預測
(4) 不是全域性最優

二、決策樹數學知識

1.資訊理論
若一事假有k種結果，對應的概率為P_i，則此事件發生後所得到的資訊量I為：

2.熵
給定包含關於某個目標概念的正反樣例的樣例集S，那麼S相對這個布林型分類的熵為：

其中P+代表正樣例，p-代表反樣例
3.條件熵
假設隨機變數（X，Y），其聯合分佈概率為P(X=xi,Y=yi)=Pij,i=1,2,⋯,n;j=1,2,⋯,m
則條件熵H(Y|X)表示在已知隨機變數X的條件下隨機變數Y的不確定性，其定義為X在給定條件下Y的條件概率分佈的熵對X的數學期望

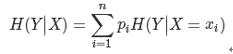
三、決策樹演算法Hunt

在Hunt演算法中，通過遞迴的方式建立決策樹。
1）如果資料集D中所有的資料都屬於一個類，那麼將該節點標記為為節點。
2）如果資料集D中包含屬於多個類的訓練資料，那麼選擇一個屬性將訓練資料劃分為較小的子集，對於測試條件的每個輸出，建立一個子女節點，並根據測試結果將D中的記錄分佈到子女節點中，然後對每一個子女節點重複1，2過程，對子女的子女依然是遞迴的呼叫該演算法，直至最後停止。

四、決策樹演算法ID3

1. 分類系統資訊熵

2. 條件熵

分類系統中的條件熵指的是當樣本的某一特徵X固定時的資訊熵
因此樣本特徵X取值為xi的概率是Pi，該特徵被固定為值xi時的條件資訊熵就是H(C|X=xi)，那麼H(C|X)就是分類系統中特徵X被固定時的條件熵（X=（x1，x2，……，xn））：

3. 資訊增益Gain(S,A)

4. 屬性選擇度量

使用資訊增益，選擇最高資訊增益的屬性作為當前節點的測試屬性

5. 演算法不足

1） 使用ID3演算法構建決策樹時，若出現各屬性值取值數分佈偏差大的情況，分類精度會大打折扣
2） ID3演算法本身並未給出處理連續資料的方法
3） ID3演算法不能處理帶有缺失值的資料集，故在演算法挖掘之前需要對資料集中的缺失值進行預處理
4） ID3演算法只有樹的生成，所以該演算法生成的樹容易產生過擬合

6.演算法流程

五、決策樹演算法C4.5

1. 屬性選擇度量

C4.5演算法用資訊增益率來選擇屬性，即選用資訊增益比選擇最佳特徵

2. 資訊增益比率度量

資訊增益比率度量是用ID3演算法中的增益度量Gain(D，X)和分裂資訊度量SplitInformation(D，X)來共同定義的。分裂資訊度量SplitInformation(D，X）就相當於特徵X（取值為x1，x2，……，xn，各自的概率為P1，P2，…，Pn，Pk就是樣本空間中特徵X取值為Xk的數量除上該樣本空間總數）的熵。
SplitInformation(D，X） = -P1 log2(P1)-P2 log2(P)-,…,-Pn log2(Pn)
GainRatio(D,X) = Gain(D,X)/SplitInformation(D,X)

3.對連續分佈特徵的處理

C4.5先把連續屬性轉換為離散屬性再進行處理。如果有N條樣本，那麼我們有N-1種離散化的方法：<=vj的分到左子樹，>vj的分到右子樹。計算這N-1種情況下最大的資訊增益率。
1）對特徵的取值進行升序排序
2）兩個特徵取值之間的中點作為可能的分裂點，將資料集分成兩部分，計算每個可能的分裂點的資訊增益（InforGain）。優化演算法就是隻計算分類屬性發生改變的那些特徵取值。
3）選擇修正後資訊增益(InforGain)最大的分裂點作為該特徵的最佳分裂點
4）計算最佳分裂點的資訊增益率（Gain Ratio）作為特徵的Gain Ratio。

4. 相比ID3演算法改進

1） 使用資訊增益比例而非資訊增益作為分裂標準
2） 處理含有帶缺失值的樣本方法為將這些值併入最常見的某一類中或以最常用的值代替
3） 處理連續值屬性
4）規則的產生：規則集儲存於一個二維陣列中，每一行代表決策樹的一個規則
5） 互動驗證：訓練開始之前，預留一部分資料，訓練之後，使用這部分資料對學習的結果進行驗證

六、葉子裁剪

1.剪枝的原因和目的

解決決策樹對訓練樣本的過擬合問題

2.決策樹常用剪枝方法

預剪枝(Pre-Pruning)和後剪枝(Post-Pruning)

3.預剪枝

預剪枝是根據一些原則及早的停止樹增長，如樹的深度達到使用者所要的深度、節點中樣本個數少於使用者指定個數、不純度指標下降的最大幅度小於使用者指定的幅度等。

4. 後剪枝

通過在完全生長的樹上剪去分枝實現的，通過刪除節點的分支來剪去樹節點，可以使用的後剪枝方法有多種，比如：代價複雜性剪枝、最小誤差剪枝、悲觀誤差剪枝等等
修剪方式有：
1）用葉子節點來替換子樹，葉節點的類別由子樹下面的多類決定
2）用子樹最常用的分支來替代子樹

七、Python sklearn實戰

1. Python Sklearn 實現

class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2,min_samples_leaf=1, max_features=None, random_state=None, min_density=None, compute_importances=None,max_leaf_nodes=None)

比較重要的引數：

• criterion ：規定了該決策樹所採用的的最佳分割屬性的判決方法，有兩種：“gini”，“entropy”。
• max_depth ：限定了決策樹的最大深度，對於防止過擬合非常有用
• min_samples_leaf ：限定了葉子節點包含的最小樣本數，這個屬性對於防止上文講到的資料碎片問題很有作用

模組中一些重要的屬性方法：

• n_classes_ ：決策樹中的類數量。
• classes_ ：返回決策樹中的所有種類標籤
• feature_importances_ ：feature的重要性，值越大，越重要
• fit(X, y, sample_mask=None, X_argsorted=None, check_input=True, sample_weight=None)
  將資料集x，和標籤集y送入分類器進行訓練，這裡要注意一個引數是：sample_weight，它和樣本的數量一樣長，所攜帶的是每個樣本的權重。
• get_params(deep=True) 得到決策樹的各個引數。
• set_params(**params) 調整決策樹的各個引數。
• predict(X) 送入樣本X，得到決策樹的預測。可以同時送入多個樣本。
• transform(X, threshold=None) 返回X的較重要的一些feature，相當於裁剪資料。
• score(X, y, sample_weight=None)
  返回在資料集X,y上的測試分數，正確率。

使用建議

• 當我們資料中的feature較多時，一定要有足夠的資料量來支撐我們的演算法，不然的話很容易overfitting
• PCA是一種避免高維資料overfitting的辦法
• 從一棵較小的樹開始探索，用export方法打印出來看看。
• 善用max_depth引數，緩慢的增加並測試模型，找出最好的那個depth。
• 善用min_samples_split和min_samples_leaf引數來控制葉子節點的樣本數量，防止overfitting。
• 平衡訓練資料中的各個種類的資料，防止一個種類的資料dominate

2 Python 實戰

測試資料data.txt
1.5 50 thin
1.5 60 fat
1.6 40 thin
1.6 60 fat
1.7 60 thin
1.7 80 fat
1.8 60 thin
1.8 90 fat
1.9 70 thin
1.9 80 fat

Python實戰程式碼
# -*- coding: utf-8 -*-
import numpy as np  
from sklearn import tree  
from sklearn.metrics import precision_recall_curve  
from sklearn.metrics import classification_report  
from sklearn.cross_validation import train_test_split  

#資料讀入
data=[]
labels=[]
with open('C:\Users\Allen\Desktop\data.txt') as ifile:
    for line in ifile:
        tokens=line.strip().split(' ')
        data.append([float(tk) for tk in tokens[:-1]])
        labels.append(tokens[-1])
x=np.array(data)
labels=np.array(labels)
y=np.zeros(labels.shape)
#標籤轉化為0,1
y[labels=='fat']=1
#拆分訓練資料和測試資料
x_train,x_test,y_train,y_test=train_test_split(x, y, test_size = 0.2) 
#使用資訊熵作為劃分標準，對決策樹進行訓練
clf=tree.DecisionTreeClassifier(criterion='entropy')
print clf
#DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=None,
            #max_features=None, max_leaf_nodes=None, min_samples_leaf=1,
            #min_samples_split=2, min_weight_fraction_leaf=0.0,
            #presort=False, random_state=None, splitter='best')
clf.fit(x_train,y_train)
#把決策樹寫入檔案  
with open("tree.dot", 'w') as f:  
    f = tree.export_graphviz(clf, out_file=f)   
# digraph Tree {
# node [shape=box] ;
# 0 [label="X[1] <= 75.0\nentropy = 0.9544\nsamples = 8\nvalue = [3, 5]"] ;
# 1 [label="X[0] <= 1.65\nentropy = 0.971\nsamples = 5\nvalue = [3, 2]"] ;
# 0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
# 2 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 2]"] ;
# 1 -> 2 ;
# 3 [label="entropy = 0.0\nsamples = 3\nvalue = [3, 0]"] ;
# 1 -> 3 ;
# 4 [label="entropy = 0.0\nsamples = 3\nvalue = [0, 3]"] ;
# 0 -> 4 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
# }
#係數反映每個特徵的影響力。越大表示該特徵在分類中起到的作用越大
print(clf.feature_importances_) 
#測試結果的列印
answer=clf.predict(x_train)
print(x_train)
print(answer)
print(y_train)
print(np.mean(answer==y_train))

#準確率與召回率
#準確率：某個類別在測試結果中被正確測試的比率
#召回率：某個類別在真實結果中被正確預測的比率
#測試結果：array([ 0.,  1.,  0.,  1.,  0.,  1.,  0.,  1.,  0.,  0.])
#真實結果：array([ 0.,  1.,  0.,  1.,  0.,  1.,  0.,  1.,  0.,  1.])
#分為thin的準確率為0.83。是因為分類器分出了6個thin，其中正確的有5個，因此分為thin的準確率為5/6=0.83。
#分為thin的召回率為1.00。是因為資料集中共有5個thin，而分類器把他們都分對了（雖然把一個fat分成了thin！），召回率5/5=1。
#分為fat的準確率為1.00。不再贅述。
#分為fat的召回率為0.80。是因為資料集中共有5個fat，而分類器只分出了4個（把一個fat分成了thin！），召回率4/5=0.80。
#本例中，目標是儘可能保證找出來的胖子是真胖子（準確率），還是保證儘可能找到更多的胖子（召回率）。
precision, recall, thresholds = precision_recall_curve(y_train, clf.predict(x_train))  
answer = clf.predict_proba(x)[:,1]  
print(classification_report(y, answer, target_names = ['thin', 'fat']))