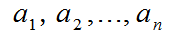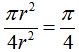演算法入門8:隨機演算法
之前將的演算法都是確定的,即對於相同的輸入總對應著相同的輸出。但實際中也常常用到不確定的演算法,比如隨機數生成演算法,演算法的結果是不確定的,我們稱這種演算法為(隨機)概率演算法,分為如下四類:
- 數值概率演算法
用於數值問題的求解,通常是近似解
- 蒙特卡洛演算法Monte Carlo
能得到問題的一個解,但不一定是正確解,正確的概率依賴於演算法執行的時間,演算法所用的時間越多,正確的概率也越高。求問題的準確解;
- 拉斯維加斯演算法 Las Vegas
不斷呼叫隨機演算法求解,直到求得正確解或呼叫次數達到某個閾值。所以,如果能得到解,一定是正確解。
- 舍伍德演算法 Sherwood
利用隨機演算法改造已有演算法,使得演算法的效能儘量與輸入資料無關,即平滑演算法的效能。它總能求得問題的一個解,且求得的解總是正確的。
1.隨機數
1. 概述
計算機產生的隨機數都是偽隨機數,通過線性同餘法得到。
方法:產生隨機序列
d稱為種子;m取值越大越好;m,b互質,常取b為質數;
2. 案例
- 偽隨機數
在實際程式設計中,我們使用rand()函式來產生隨機數,rand()函式返回0到一個最大值之間的一個隨機數。
#include <stdio.h> #include <stdlib.h> #include <time.h> //產生[0,100)的隨機數 void GenerateRandomNumber() { for(int i=0;i<10;i++) { printf("%-4d",rand()%100);//產生[0,m)的隨機數 } printf("\n"); } int main() { GenerateRandomNumber(); return 0; }
執行程式碼,輸出:41 67 34 0 69 24 78 58 62 64
如果我們重複執行程式碼就會發現,每次的輸出結果都是這個序列。這就是因為rand產生的隨機序列是偽隨機序列。解決方法是:使用當前的時間作為隨機種子。
- 時間作為隨機種子
srand((unsigned)time(0));//以當前時間作為種子2. 數值概率演算法的應用
(1)隨機投點法計算π
(2)計算定積分
(3)解非線性方程組
1. 隨機投點法計算π
如下圖,正方形及其內切圓,圓半徑為r。現向正方形中隨機投n個點,所投點均勻分佈,則點落入圓內概率為
考慮第一象限即可,取r=1,投n個點,落入圓中k個點,當n趨近無窮時,k/n 趨近於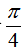
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <assert.h>
float CalculatePI(int n)
{
assert(n>0);
int i=0,k=0;
float x,y;
srand((unsigned)time(NULL));
for(i=0;i<n;i++)
{
//隨機點
x = (float)(rand()%10000)/10000;//x座標,[0,1)
y = (float)(rand()%10000)/10000;//y座標,[0,1)
//判斷是否落在圓內
if(x*x+y*y<=1)
k++;
}
// pi/4 = k/n , pi=4*(k/n)
printf("n=%-10d k=%-10d ",n,k);
return (float)4*k/n;
}
int main()
{
printf("pi=%f\n",CalculatePI(10));
printf("pi=%f\n",CalculatePI(1000));
printf("pi=%f\n",CalculatePI(10000000));
return 0;
}
一次執行結果如下:
n=10 k=10 pi=4.000000
n=1000 k=825 pi=3.300000
n=10000000 k=8184707 pi=3.273883
2. 計算定積分
原理和計算π相同,對積分函式f(x)有約束條件:1. 在積分割槽域內連續;2. 在積分割槽域記憶體在最大最小值。
3. 舍伍德(Sherwood)演算法
一個演算法,對於不同的輸入資料,其演算法的效能是不一樣的。比如快排演算法,每次選擇第一個元素作為基準,對序列從小到大排序:
平均情況:如果待排序列無序,則演算法時間複雜度為O(nlogn);
最壞情況:如果序列有序(正序或逆序),則演算法時間複雜度為O(n2)
舍伍德演算法的思想是:設計隨機演算法,使得演算法的效能和具體的輸入值無關,演算法的效能 =平均效能 + 一個很小的隨機值。
舍伍德演算法是為了得到好的平均效能。
準確的說:它是一種思想,並不是一個具體的實現案例。
利用隨機演算法可將一個演算法改造成舍伍德演算法,比如,快速排序時,基準的選擇可以使用隨機演算法得到。
對於不能直接改造的,可以引入隨機預處理,即對輸入進行隨機洗牌。比如,對於通常的排序、查詢演算法,可以先對待排序、查詢的序列進行隨機位置置換(洗牌)。
可見舍伍德演算法就是一種利用隨機演算法改造確定性演算法,使得演算法的效能和輸入資料儘量無關。
4.拉斯維加斯(Las Vegas)演算法演算法思想就是不斷呼叫隨機演算法求解,直到求得正確解或者達到設定的步數。
【理解為:不斷擲骰子,直到得到某個值,或擲累了】
如下面的程式碼:success=false;steps=0;
while(!success && (steps++)<MAX_STEP)
{
success = RandomSovle();//隨機演算法求解問題
}
拉斯維加斯演算法不一定能獲得解,隨著執行時間的增加,獲得解的概率也越大。
它可以用來求解某些迄今沒有有效解法的問題,因為通過不斷的隨機嘗試,也許能夠找到正確解。
5. 蒙特卡羅(Monte Carlo)演算法拉斯維加斯演算法是:不一定能給出解,給出則必正確
蒙特卡羅演算法是:一定能給出解,但不一定正確
蒙特卡羅演算法在一般情況下能夠保證對問題的所有例項都以高概率給出正確解。但是,通常無法判斷一個具體解是否正確。
一個蒙特卡羅演算法得到正確解的概率為p,如果0.5 < p < 1,則稱演算法是正確的。p-0.5稱為演算法的優勢。
對於用一個例項,如果蒙特卡羅演算法不會給出兩個不同的正確解,則稱演算法是一致的。
轉載本文請註明作者和出處
作者 :JarvisChu