[深度學習]深度自編碼器簡述
自從Hinton 2006年的工作之後,越來越多的研究者開始關注各種自編碼器模型相應的堆疊模型。實際上,自編碼器(Auto-Encoder)是一個較早的概念了,比如Hinton等人在1986, 1989年的工作。(說來說去都是這些人吶。。。)
自編碼器簡介
先暫且不談神經網路、深度學習,僅是自編碼器的話,其原理很簡單。自編碼器可以理解為一個試圖去還原其原始輸入的系統。如下圖所示。
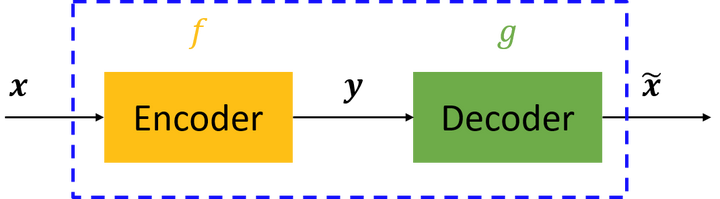
圖中,虛線藍色框內就是一個自編碼器模型,它由編碼器(Encoder)和解碼器(Decoder)兩部分組成,本質上都是對輸入訊號做某種變換。編碼器將輸入訊號x變換成編碼訊號y,而解碼器將編碼y轉換成輸出訊號。即
y=f(x)
而自編碼器的目的是,讓輸出儘可能復現輸入x,即tries to copy its input to its output。但是,這樣問題就來了——如果f和g都是恆等對映,那不就恆有
=x了?不錯,確實如此,但這樣的變換——沒有任何卵用啊!因此,我們經常對中間訊號y(也叫作“編碼”)做一定的約束,這樣,系統往往能學出很有趣的編碼變換f和編碼y。
這裡強調一點,對於自編碼器,我們往往並不關係輸出是啥(反正只是復現輸入),我們真正關心的是中間層的編碼,或者說是從輸入到編碼的對映。可以這麼想,在我們強迫編碼y和輸入x不同的情況下,系統還能夠去復原原始訊號x,那麼說明編碼y已經承載了原始資料的所有資訊,但以一種不同的形式!這就是特徵提取啊,而且是自動學出來的!實際上,自動學習原始資料的特徵表達也是神經網路和深度學習的核心目的之一。
為了更好的理解自編碼器,下面結合神經網路加以介紹。
自編碼器與神經網路
神經網路的知識不再詳細介紹,相信瞭解自編碼器的讀者或多或少會了解一些。簡單來講,神經網路就是在對原始訊號逐層地做非線性變換,如下圖所示。
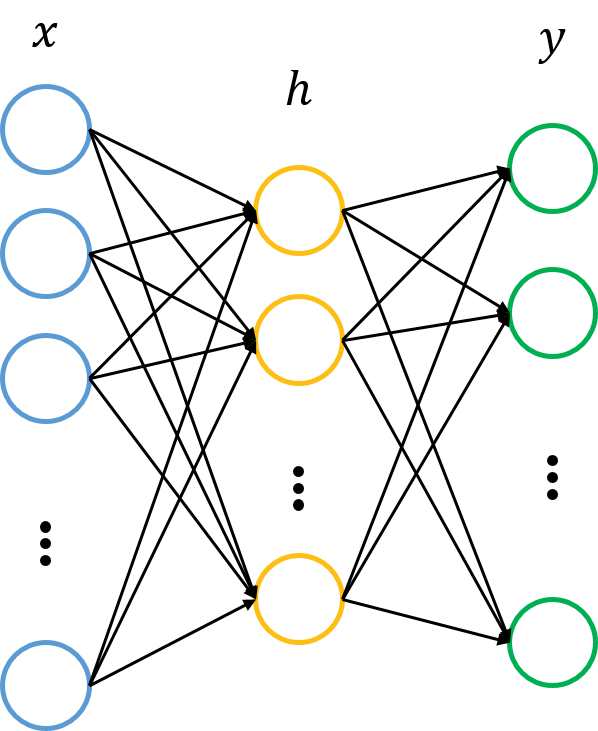
該網路把輸入層資料x∈Rn轉換到中間層(隱層)h∈Rp,再轉換到輸出層y∈Rm。圖中的每個節點代表資料的一個維度(偏置項圖中未標出)。每兩層之間的變換都是“線性變化”+“非線性啟用”,用公式表示即為
h=f(W(1)x+b(1))
y=f(W(2)h+b(2))
神經網路往往用於分類,其目的是去逼近從輸入層到輸出層的變換函式。因此,我們會定義一個目標函式來衡量當前的輸出和真實結果的差異,利用該函式去逐步調整(如梯度下降)系統的引數(W(1),b(1),W(2),b(2)),以使得整個網路儘可能去擬合訓練資料。如果有正則約束的話,還同時要求模型儘量簡單(防止過擬合)。
那麼,自編碼器怎麼表示呢?前面已說過,自編碼器試圖復現其原始輸入,因此,在訓練中,網路中的輸出應與輸入相同,即y=x,因此,一個自編碼器的輸入、輸出應有相同的結構,即
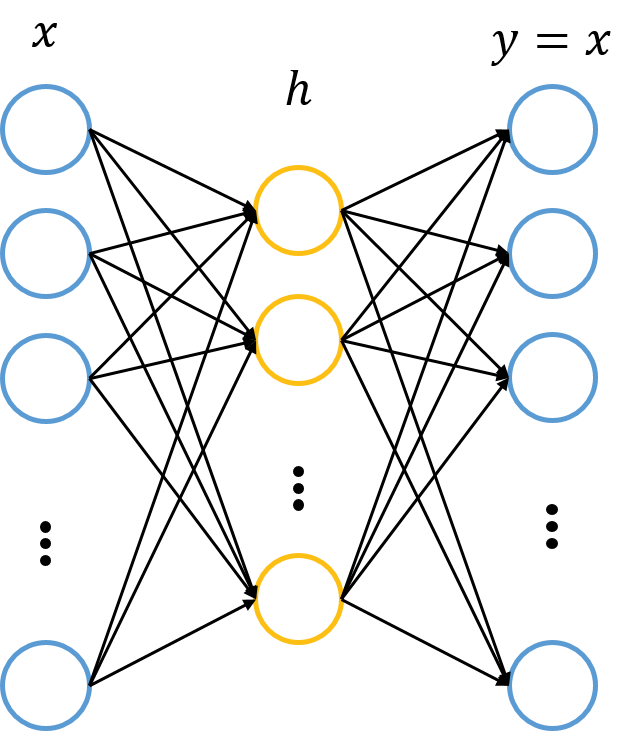
我們利用訓練資料訓練這個網路,等訓練結束後,這個網路即學習出了x→h→x的能力。對我們來說,此時的h是至關重要的,因為它是在儘量不損失資訊量的情況下,對原始資料的另一種表達。結合神經網路的慣例,我們再將自編碼器的公式表示如下:(假設啟用函式是sigmoid,用s表示)
y=fθ(x)=s(Wx+b)
L(x,
其中,L表示損失函式,結合資料的不同形式,可以是二次誤差(squared error loss)或交叉熵誤差(cross entropy loss)。如果,一般稱為tied weights。
為了儘量學到有意義的表達,我們會給隱層加入一定的約束。從資料維度來看,常見以下兩種情況:
- n>p,即隱層維度小於輸入資料維度。也就是說從x→h的變換是一種降維的操作,網路試圖以更小的維度去描述原始資料而儘量不損失資料資訊。實際上,當每兩層之間的變換均為線性,且監督訓練的誤差是二次型誤差時,該網路等價於PCA!沒反應過來的童鞋可以反思下PCA是在做什麼事情。
- n<p,即隱層維度大於輸入資料維度。這又有什麼用呢?其實不好說,但比如我們同時約束h的表達儘量稀疏(有大量維度為0,未被啟用),此時的編碼器便是大名鼎鼎的“稀疏自編碼器”。可為什麼稀疏的表達就是好的?這就說來話長了,有人試圖從人腦機理對比,即人類神經系統在某一刺激下,大部分神經元是被抑制的。個人覺得,從特徵的角度來看更直觀些,稀疏的表達意味著系統在嘗試去特徵選擇,找出大量維度中真正重要的若干維。
堆疊自編碼器
有過深度學習基礎的童鞋想必瞭解,深層網路的威力在於其能夠逐層地學習原始資料的多種表達。每一層的都以底一層的表達為基礎,但往往更抽象,更加適合複雜的分類等任務。
堆疊自編碼器實際上就在做這樣的事情,如前所述,單個自編碼器通過虛構x→h→x的三層網路,能夠學習出一種特徵變化h=fθ(x)(這裡用θ表示變換的引數,包括W,b和啟用函式)。實際上,當訓練結束後,輸出層已經沒什麼意義了,我們一般將其去掉,即將自編碼器表示為
之前之所以將自編碼器模型表示為3層的神經網路,那是因為訓練的需要,我們將原始資料作為假想的目標輸出,以此構建監督誤差來訓練整個網路。等訓練結束後,輸出層就可以去掉了,我們關心的只是從x到h的變換。
接下來的思路就很自然了——我們已經得到特徵表達h,那麼我們可不可以將
h再當做原始資訊,訓練一個新的自編碼器,得到新的特徵表達呢?當然可以!這就是所謂的堆疊自編碼器(Stacked Auto-Encoder, SAE)。Stacked就是逐層壘疊的意思,跟“棧”有點像。UFLDL教程將其翻譯為“棧式自編碼”,anyway,不管怎麼稱呼,都是這個東東,別被花裡胡哨的專業術語嚇到就行。當把多個自編碼器Stack起來之後,這個系統看起來就像這樣:

亦可賽艇!這個系統實際上已經有點深度學習的味道了,即learning multiple levels of representation and abstraction(Hinton, Bengio, LeCun, 2015)。需要注意的是,整個網路的訓練不是一蹴而就的,而是逐層進行。按題主提到的結構n,m,k結構,實際上我們是先訓練網路n→m→n,得到n→m的變換,然後再訓練m→k→m,得到m→k的變換。最終堆疊成SAE,即為n→m→k的結果,整個過程就像一層層往上蓋房子,這便是大名鼎鼎的layer-wise unsuperwised pre-training(逐層非監督預訓練),正是導致深度學習(神經網路)在2006年第3次興起的核心技術。
關於逐層預訓練與深度學習,將在本文最後探討。
自編碼器的變種形式
上述介紹的自編碼器是最基本的形式。善於思考的童鞋可能已經意識到了這個問題:隱層的維度到底怎麼確定?為什麼稀疏的特徵比較好?或者更準確的說,怎麼才能稱得上是一個好的表達(What defines a good representation)?
事實上,這個問題回答並不唯一,也正是從不同的角度去思考這個問題,導致了自編碼器的各種變種形式出現。目前常見的幾種模型總結如下(有些術語實在不好翻譯,看英文就好。。。)

下面簡介下其中兩種模型,以對這些變種模型有個直觀感受。
稀疏自編碼器
UFLDL-自編碼演算法與稀疏性對該模型有著比較詳細的介紹。如前所示,這種模型背後的思想是,高維而稀疏的表達是好的。一般而言,我們不會指定隱層表達h中哪些節點是被抑制的(對於sigmoid單元即輸出為0),而是指定一個稀疏性引數ρ,代表隱藏神經元的平均活躍程度(在訓練集上取平均)。比如,當ρ=0.05時,可以認為隱層節點在95%的時間裡都是被一直的,只有5%的機會被啟用。實際上,為了滿足這一條件,隱層神經元的活躍度需要接近於0。
那麼,怎麼從數學模型上做到這點呢?思路也不復雜,既然要求平均啟用度為ρ,那麼只要引入一個度量,來衡量神經元ii的實際啟用度與期望啟用度ρ之間的差異即可,然後將這個度量新增到目標函式作為正則,訓練整個網路即可。那麼,什麼樣的度量適合這個任務呢?有過概率論、資訊理論基礎的同學應該很容易想到它——相對熵,也就是KL散度(KL
divergence)。因此,整個網路所新增的懲罰項即為
具體的公式不再展開,可以從下圖(摘自UFLDL)中直觀理解KL散度作為懲罰項的含義。圖中假設平均啟用度ρ=0.2。
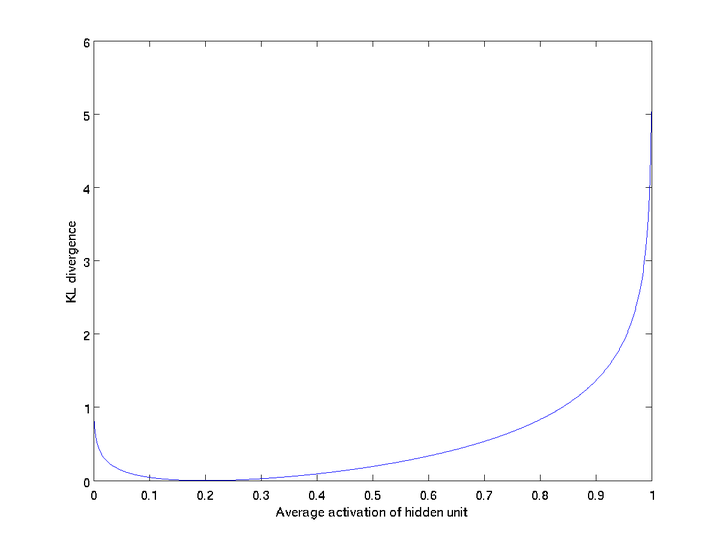
可以看出,當^ρiρ^i一旦偏離期望啟用度ρρ,這種誤差便急劇增大,從而作為懲罰項新增到目標函式,指導整個網路學習出稀疏的特徵表達。
降噪自編碼器
關於降噪自編碼器,強烈推薦其作者Pascal Vincent的論文Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion。DAE的核心思想是,一個能夠從中恢復出原始訊號的表達未必是最好的,能夠對“被汙染/破壞”的原始資料編碼、解碼,然後還能恢復真正的原始資料,這樣的特徵才是好的。
稍微數學一點,假設原始資料x被我們“故意破壞”,比如加入高斯白噪,或者把某些維度資料抹掉,變成了,然後再對
編碼、解碼,得到恢復訊號
,該恢復訊號儘可能逼近未被汙染的資料xx。此時,監督訓練的誤差從L(x,g(f(x)))變成了L(x,g(f(
)))。
直觀上理解,DAE希望學到的特徵變換儘可能魯棒,能夠在一定程度上對抗原始資料的汙染、缺失。Vincent論文裡也對DAE提出了基於流行的解釋,並且在影象資料上進行測試,發現DAE能夠學出類似Gabor邊緣提取的特徵變換。注意,這一切都是在我們定義好規則、誤差後,系統自動學出來的!從而避免了領域專家費盡心力去設計這些效能良好的特徵。
DAE的系統結構如下圖(摘自Vincent論文)所示。
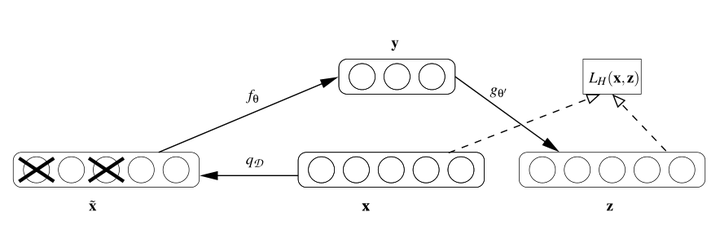
現在使用比較多的noise主要是mask noise,即原始資料中部分資料缺失,這是有著很強的實際意義的,比如影象部分畫素被遮擋、文字因記錄原因漏掉了一些單詞等等。
其他的模型就不再展開了,總之,每遇到一個自編碼器的一個變種模型時,搞清楚其背後的思想(什麼樣的表達才是好的),就很容易掌握了。套用V的”Behind this mask is a man, and behind this man is an idea, and ideas are bulletproof”,我們可以說,”Behind this auto-encoder is a model, and behind this model is an idea, and ideas are bulletproof”。
關於預訓練與深度學習
深度學習第3次興起正式因為逐層預訓練方法的提出,使得深度網路的訓練成為可能。對於一個深度網路,這種逐層預訓練的方法,正是前面介紹的這種Stacked Auto-Encoder。對於常見的分類任務,一般分為以下兩個階段:
- layer-wise pre-training (逐層預訓練)
- fune-tuning (微調)
注意到,前述的各種SAE,本質上都是非監督學習,SAE各層的輸出都是原始資料的不同表達。對於分類任務,往往在SAE頂端再新增一分類層(如Softmax層),並結合有標註的訓練資料,在誤差函式的指導下,對系統的引數進行微調,以使得整個網路能夠完成所需的分類任務。

對於微調過程,即可以只調整分類層的引數(此時相當於把整個SAE當做一個feature extractor),也可以調整整個網路的引數(適合訓練資料量比較大的情況)。
題主提到,為什麼訓練稀疏自編碼器為什麼一般都是3層的結構,實際上這裡的3層是指訓練單個自編碼器所假想的3層神經網路,這對任何基於神經網路的編碼器都是如此。多層的稀疏自編碼器自然是有的,只不過是通過layer-wise pre-training這種方式逐層壘疊起來的,而不是直接去訓練一個5層或是更多層的網路。
為什麼要這樣?實際上,這正是在訓練深層神經網路中遇到的問題。直接去訓練一個深層的自編碼器,其實本質上就是在做深度網路的訓練,由於梯度擴散等問題,這樣的網路往往根本無法訓練。這倒不是因為會破壞稀疏性等原因,只要網路能夠訓練,對模型施加的約束總能得到相應的結果。
但為什麼逐層預訓練就可以使得深度網路的訓練成為可能了呢?有不少文章也做過這方面的研究。一個直觀的解釋是,預訓練好的網路在一定程度上擬合了訓練資料的結構,這使得整個網路的初始值是在一個合適的狀態,便於有監督階段加快迭代收斂。
筆者曾經基於 MNIST資料集,嘗試了一個9層的網路完成分類任務。當隨機初始化時,誤差傳到底層幾乎全為0,根本無法訓練。但採用逐層預訓練的方法,訓練好每兩層之間的自編碼變換,將其引數作為系統初始值,然後網路在有監督階段就能比較穩定的迭代了。
當然,有不少研究提出了很好的初始化策略,再加上現在常用的dropout、ReLU,直接去訓練一個深層網路已經不是問題。這是否意味著這種逐層預訓練的方式已經過時了呢?這裡,我想採用下Bengio先生2015年的一段話作為回答:
Stacks of unsupervised feature learning layers are STILL useful when you are in a regime with insufficient labeled examples, for transfer learning or domain adaptation. It is a regularizer. But when the number of labeled examples becomes large enough, the advantage of that regularizer becomes much less. I suspect however that this story is far from ended! There are other ways besides pre-training of combining supervised and unsupervised learning, and I believe that we still have a lot to improve in terms of our unsupervised learning algorithms.
最後,多說一句,除了AE和SAE這種逐層預訓練的方式外,還有另外一條類似的主線,即限制玻爾茲曼機(RBM)與深度信念網路(DBN)。這些模型在神經網路/深度學習框架中的位置,可以簡要總結為下圖。
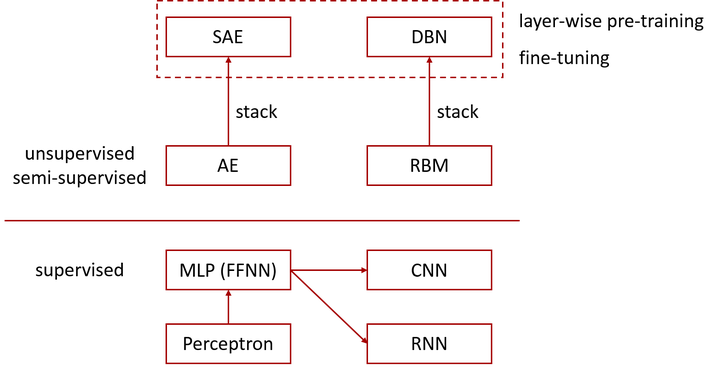
訂正:感謝@Detective 夏恩指正,RBM堆疊起來是Deep Boltzmann Machines, 再加一個分類器才是DBN,供閱讀上圖時參考。
相關學習資料推薦
- Hinton, G.E. and R.R. Salakhutdinov, Reducing the dimensionality of data with neural networks. Science, 2006. 313(5786): p. 504-507.
- Learning multiple layers of representation. Trends in cognitive sciences, 2007. 11(10): p. 428-434.
- Vincent, P., et al. Extracting and composing robust features with denoising autoencoders. in Proceedings of the 25th international conference on Machine learning. 2008.
- Bengio, Y., Learning deep architectures for AI. Foundations and trends? in Machine Learning, 2009. 2(1): p. 1-127.
- Vincent, P., et al., Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. Journal of Machine Learning Research, 2010. 11(6): p.3371-3408.
- Rifai, S., et al., Contractive Auto-Encoders: Explicit Invariance During Feature Extraction. Icml, 2011.
- Chen, M., et al., Marginalized denoising autoencoders for domain adaptation. arXiv preprint arXiv:1206.4683, 2012.
- Bengio, Y., A. Courville and P. Vincent, Representation learning: A review and new perspectives. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2013. 35(8): p.1798-1828.
- LeCun, Y., Y. Bengio and G. Hinton, Deep learning. Nature, 2015. 521(7553): p. 436-444.
