卡方值的計算與意義

　　χ²值表示觀察值與理論值之問的偏離程度。計算這種偏離程度的基本思路如下。

　　(1)設A代表某個類別的觀察頻數，E代表基於H₀計算出的期望頻數，A與E之差稱為殘差。

　　(2)顯然，殘差可以表示某一個類別觀察值和理論值的偏離程度，但如果將殘差簡單相加以表示各類別觀察頻數與期望頻數的差別，則有一定的不足之處。因為殘差有正有負，相加後會彼此抵消，總和仍然為0，為此可以將殘差平方後求和。

　　(3)另一方面，殘差大小是一個相對的概念，相對於期望頻數為10時，期望頻數為20的殘差非常大，但相對於期望頻數為1 000時20的殘差就很小了。考慮到這一點，人們又將殘差平方除以期望頻數再求和，以估計觀察頻數與期望頻數的差別。

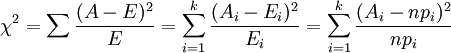　　(i=1，2，3，…，k)

　　其中，A_i為i水平的觀察頻數，E_i為i水平的期望頻數，n為總頻數，p_i為i水平的期望頻率。i水平的期望頻數T_i等於總頻數n×i水平的期望概率p_i，k為單元格數。當n比較大時，χ²統計量近似服從k-1(計算E_i時用到的引數個數)個自由度的卡方分佈。

　　作為學術界的領袖，Pearson先生當初發表在《哲學雜誌》上的χ²論文題目為：On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling.

　　由卡方的計算公式可知，當觀察頻數與期望頻數完全一致時，χ²值為0；觀察頻數與期望頻數越接近，兩者之間的差異越小，χ²值越小；反之，觀察頻數與期望頻數差別越大，兩者之間的差異越大，χ²值越大。換言之，大的χ²值表明觀察頻數遠離期望頻數，即表明遠離假設。小的χ²值表明觀察頻數接近期望頻數，接近假設。因此，χ²是觀察頻數與期望頻數之間距離的一種度量指標，也是假設成立與否的度量指標。如果χ²值“小”，研究者就傾向於不拒絕H₀；如果χ²值大，就傾向於拒絕H₀。至於χ²在每個具體研究中究竟要大到什麼程度才能拒絕H₀，則要藉助於卡方分佈求出所對應的P值來確定。