1. 層次聚類

層次聚類演算法與之前所講的順序聚類有很大不同，它不再產生單一聚類，而是產生一個聚類層次。說白了就是一棵層次樹。介紹層次聚類之前，要先介紹一個概念——巢狀聚類。講的簡單點，聚類的巢狀與程式的巢狀一樣，一個聚類中R₁包含了另一個R₂，那這就是R₂巢狀在R₁中，或者說是R₁嵌套了R₂。具體說怎麼算巢狀呢？聚類R₁={{x₁,x₂},{x₃},{x₄,x₅}巢狀在聚類R₂={{x₁,x₂,x₃},{x₄,x₅}}中，但並不巢狀在聚類R₃={{x₁,x₄},{x₃},{x₂,x₅}}中。

層次聚類演算法產生一個巢狀聚類的層次，演算法最多包含N步，在第t步，執行的操作就是在前t-1步的聚類基礎上生成新聚類。主要有合併和分裂兩種實現。我這裡只講合併，因為前一階段正好課題用到，另外就是合併更容易理解和實現。當然分裂其實就是合併的相反過程。

令g(C_i,C_j)為所有可能的X聚類對的函式，此函式用於測量兩個聚類之間的近鄰性，用t表示當前聚類的層次級別。通用合併演算法的偽碼描述如下：

1. 初始化：

a) 選擇Â₀={{x₁},…,{x_N}}

b) 令t=0

2. 重複執行以下步驟：

a) t=t+1

b) 在Â_t-1中選擇一組(C_i,C_j)，滿足

c) 定義C_q=C_iÈC_j，並且產生新聚類Â_t=(Â_t-1-{C_i,C_j})È{C_q}

直到所有向量全被加入到單一聚類中。

這一方法在t層時將兩個向量合併，那麼這兩個向量在以後的聚類過程中的後繼聚類都是相同的，也就是說一旦它們走到一起，那麼以後就不會再分離……（很專一哦O(∩_∩)O~）。這也就引出了這個演算法的缺點，當在演算法開始階段，若出現聚類錯誤，那麼這種錯誤將一直會被延續，無法修改。在層次t上，有N-t個聚類，為了確定t+1層上要合併的聚類對，必須考慮(N-t)(N-t-1)/2個聚類對。這樣，聚類過程總共要考慮的聚類對數量就是(N-1)N(N+1)/6，也就是說整個演算法的時間複雜度是O(N³

舉例來說，如果令X={x₁, x₂, x₃, x₄, x₅}，其中x₁=[1, 1]^T, x₂=[2, 1]^T, x₃=[5, 4]^T, x₄=[6, 5]^T, x₅=[6.5, 6]^T。那麼合併演算法執行的過程可以用下面的圖來表示。

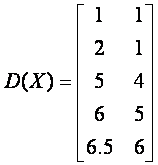
     P(X)是不相似矩陣

該演算法從核心過程上來講，就是先計算出資料集中向量之間的距離，記為距離矩陣（也叫不相似矩陣）。接著通過不斷的對矩陣更新，完成聚類。矩陣更新演算法的偽碼描述如下：

1. 初始化：

a) Â₀={{x₁},…,{x_N}}

b) P₀=P(X) (距離矩陣)

c) t=0

2. 重複執行以下步驟：

a) t=t+1

b) 合併C_i

c) 刪除第i和j行，第i和j列，同時插入新的行和列，新的行列為新合併的類C_q與所有其他聚類之間的距離值

直到將所有向量合併到一個聚類中

大家可以看到，層次聚類演算法的輸出結果總是一個聚類，這往往不是我們想要的，我們總希望演算法在得到我們期望的結果後就停止。那麼我們如何控制呢？常用的做法就是為演算法限制一個閾值，矩陣更新過程中，總是將兩個距離最近的聚類合併，那麼我們只要加入一個閾值判斷，當這個距離大於閾值時，就說明不需要再合併了，此時演算法結束。這樣的閾值引入可以很好的控制演算法結束時間，將層次截斷在某一層上。

2. 演算法實現

       MATLAB實現了層次聚類演算法，基本語句如下：

1X = [1 2;2.5 4.5;2 2;4 1.5;4 2.5] ; 
2Y = pdist(X,'euclid');  
3Z = linkage(Y,'single');  
4T = cluster(Z,'cutoff',cutoff);

MATLAB還有一個簡化的層次聚類版本，一句話搞定

1T = clusterdata(X,cutoff)