神經網路引數更新
一、引數更新
1.隨機梯度下降及各種更新方法
【普通更新】:沿著負梯度方向改變引數
x+= -learning_rate * dx
其中學習率是一個超引數,它是一個固定的常量。
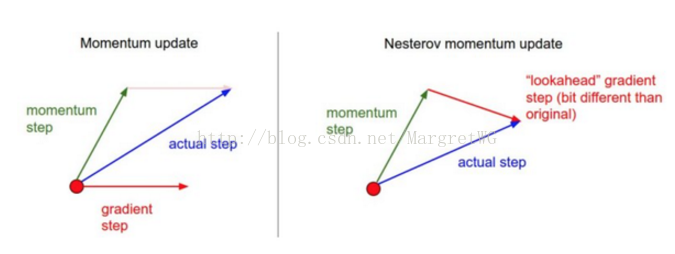
【動量更新】(Momentum)
這個方法在深度網路上幾乎總能得到更好的收斂速度。是從物理角度上對最優化問題得到的啟發。它將損失值理解為是山的高度(因此高度勢能是U=mgh,所以U正比於h)用隨機數字初始化引數等同於在某個位置給質點設定初始速度為0,這樣,最優化過程可以看做是模擬引數向量(即質點)在地形上滾動的過程
因為作用於質點的力與梯度的潛在能量(F=-▽U)有關,質點所受的力就是損失函式的(負)梯度。
# 動量更新
v = mu * v - learning_rate * dx # 與速度融合
x += v # 與位置融合
【Nesterov動量】
核心思路: 但當引數向量位於某個位置x時,由上述公式知,動量部分會通過mu*v稍微改變引數向量。因此,如果要計算梯度,那麼可以將未來的近似位置x+mu*V看做是“向前看”,這個點在我們一會要停止的位置附近,因此計算x+mu*v的梯度而不是舊位置x的梯度就有意義了。
如右圖,既然我們知道動量將會把我們帶到綠色箭頭指向的店,我們就不要再遠點(紅色點)那裡計算梯度了。
x_ahead = x + mu * v
# 計算dx_ahead(在x_ahead處的梯度,而不是在x處的梯度)
v = mu * v - learning_rate * dx_ahead 實際應用中,通過對x_ahead=x+mu*v使用變數變化進行改寫,然後用x_ahead而不是x來表示上面的更新,也就是說實際儲存的引數向量總是向前一步的那個版本,x_ahead(將其重新命名為x)的公式就變成了:
v_prev = v # 儲存備份
v = mu * v - learning_rate * dx # 速度更新保持不變
x += -mu * v_prev + (1 + mu) * v # 位置更新變了形式二、學習率退火
如果學習率過高,系統的動能就過大,引數向量就會無規律地跳動,不能夠穩定到損失函式更深更窄的部分去。實現學習率退火有3種方式:
1.隨步數衰減
典型的值是每過5個週期就將學習率減小一半,但這要依賴具體問題和模型的選擇。有一種經驗做法:使用一個固定的學習率來進行訓練的同時觀察驗證集錯誤率,每當驗證集錯誤率停止下降,就乘以一個常數(0.5)來降低學習率
2.指數衰減
,t是迭代次數
3.1/t衰減
三、二階方法
基於牛頓法,其迭代如下:
Hf(x)是函式的二階偏導數的平方矩陣,▽f(x)是梯度向量,直觀理解Hf(x)描述了損失函式的局部曲率,從而使得可以進行更高效的引數更新。使得在曲率大的時候小步前進,曲率小的時候大步前進。但一個巨大難題在於要計算矩陣的逆,這是非常耗時的。這樣,各種各樣的擬-牛頓方法就被髮明出來,最流行的是L-BFGS.
四、逐引數適應學習率方法
前面討論都是對學習率進行全域性地操作,並且對所有的引數都是一樣的。有一些人發明了能夠適應性對學習率調參的方法,甚至是逐個引數適應學習率調參。如下是一些常用的適應演算法
1.Adagrad
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)接收到高梯度值的權重更新的效果被減弱,而接受到低梯度值的權重的更新效果將會增強
2.RMSprop
簡單修改了Adagrad方法,讓它不那麼激進,總體來說,就是是使用了一個梯度平方的滑動平均:
cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)3.Adam
像是RMSprop的動量版
m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)五、超引數調優
神經網路最常用的超引數有:
- 初始學習率
- 學習率衰減方式(例如一個衰減常量)
- 正則化強度(L2懲罰,隨機失活強度)
超引數範圍
在對數尺度上進行超引數搜尋。例如,一個典型的學習率應該看起來是這樣:learning_rate=10** uniform(-6,1),因為學習率乘以了計算出的梯度,因此,比起加上或者減少某些值,思考學習率的範圍是乘以或者除以某些值更加自然。但是有一些引數(比如隨機失活概率)還是在原始尺度上進行搜尋
隨機搜尋優於網路搜尋
對於邊界上的最優值要小心,這種情況一般發生在你在一個不好的範圍內搜尋超引數。比如,假設我們使用learning_rate=10** uniform(-6,1)來進行搜尋。一旦我們得到一個比較好的值,一定要確認你的值不是出於這個範圍的邊界上。
從粗到細地分階段搜尋。在實踐中,先進行初略範圍搜尋,然後根據好的結果出現的地方,縮小範圍進行搜尋。進行粗搜尋的時候,讓模型訓練一個週期就可以了,小範圍搜尋時,可以讓模型執行5個週期,而最後一個階段就在最終的範圍內進行仔細搜尋,執行多次週期。
六、評價
模型整合
在實踐的時候,有一個總是能提升神經網路幾個百分點準確率的辦法,就是在訓練的時候訓練幾個獨立的模型,然後在測試的時候平均它們預測結果。整合的模型數量增加,演算法的結果也單調提升(但提升效果越來越少)。還有模型之間的差異度越大,提升效果可能越好。進行整合有以下幾種方法:
- 同一個模型,不同的初始化:使用交叉驗證來得到最好的超引數,然後用最好的引數來訓練不同初始化條件的模型
- 在交叉驗證中發現最好的模型:使用交叉驗證來得到最好的超引數,然後取其中最好的幾個(比如10個)模型來進行整合。這樣就提高了整合的多樣性,實際操作中,這樣操作起來比較簡單,在交叉驗證後就不需要額外的訓練
- 一個模型設定多個記錄點:如果訓練非常耗時,那就在不同的訓練時間對網路留下記錄點(比如每個週期結束),然後用它們來進行模型整合。很顯然,這樣做多樣性不足,但是在實踐中效果還是不錯的,這種方法的優勢是代價比較小
- 在訓練的時候跑引數的平均值:這個方法就是在訓練過程中,如果損失值相較於前一次權重出現指數下降時,就在記憶體中對網路的權重進行一次備份,這樣你就對前幾次迴圈中的網路狀態進行了平均。你會發現這個“平滑”過的版本的權重總是能得到更少的誤差。
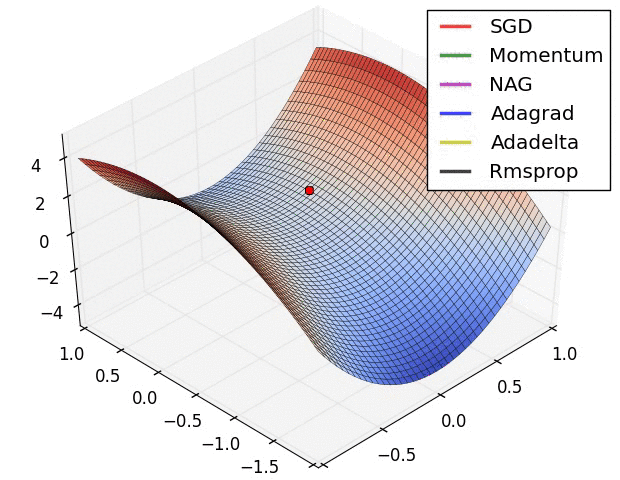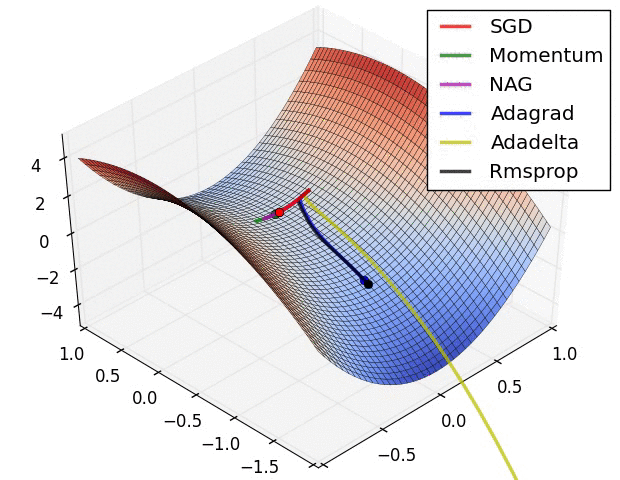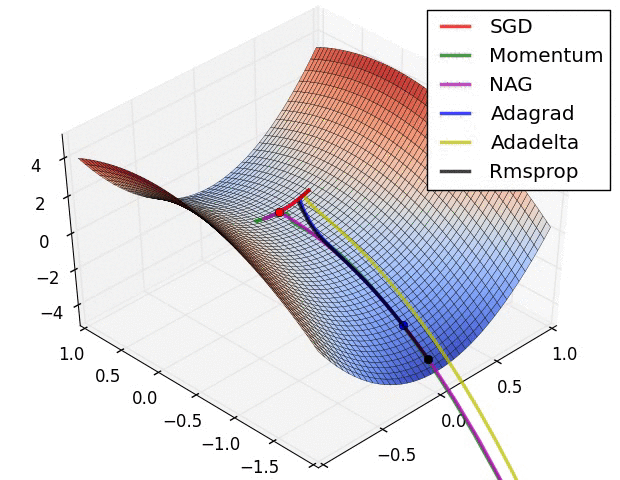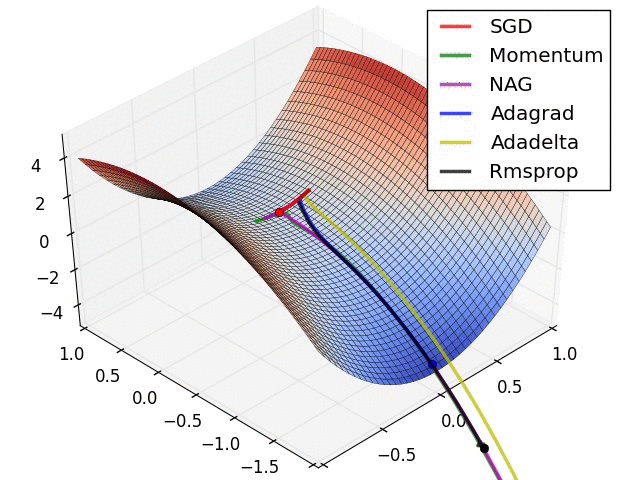
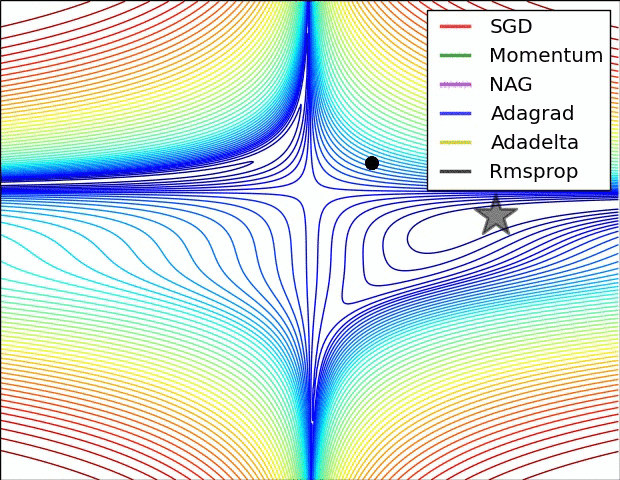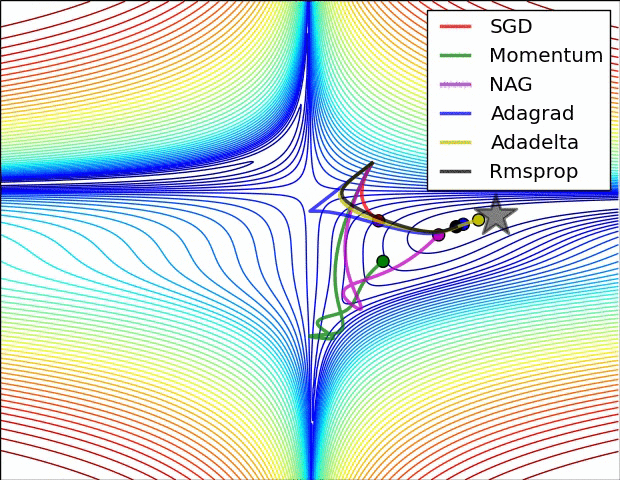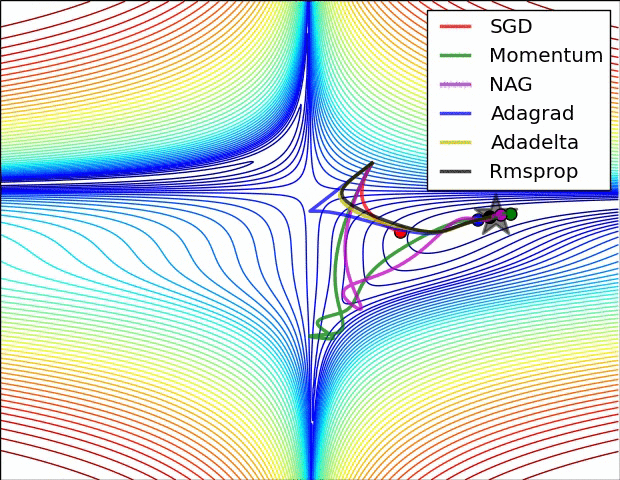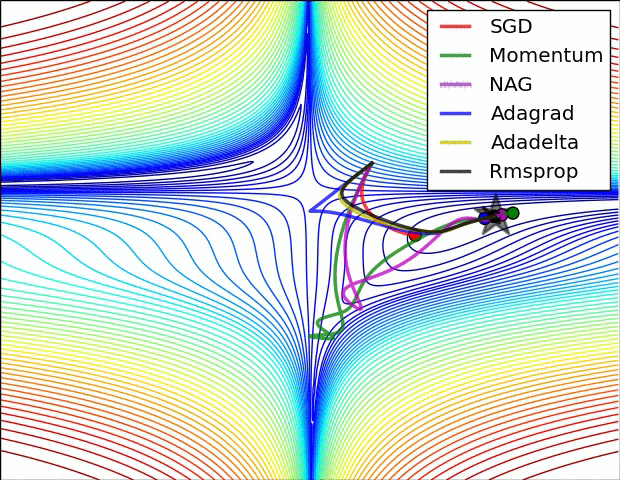
【這兩幅動圖幫助你理解學習的動態過程】
七、總結
訓練一個神經網路需要:
-
利用小批量資料對實現進行梯度檢查,還要注意各種錯誤。
-
進行合理性檢查,確認初始損失值是合理的,在小資料集上能得到100%的準確率。
-
在訓練時,跟蹤損失函式值,訓練集和驗證集準確率,如果願意,還可以跟蹤更新的引數量相對於總引數量的比例(一般在1e-3左右),然後如果是對於卷積神經網路,可以將第一層的權重視覺化。
-
推薦的兩個更新方法是SGD+Nesterov動量方法,或者Adam方法。
-
隨著訓練進行學習率衰減。比如,在固定多少個週期後讓學習率減半,或者當驗證集準確率下降的時候。
-
使用隨機搜尋(不要用網格搜尋)來搜尋最優的超引數。分階段從粗(比較寬的超引數範圍訓練1-5個週期)到細(窄範圍訓練很多個週期)地來搜尋。
-
進行模型整合來獲得額外的效能提高。