深層神經網路引數初始化方式對訓練精度的影響
阿新 • • 發佈：2019-01-24
本文是基於吳恩達老師《深度學習》第二週第一課練習題所做，目的在於探究引數初始化對模型精度的影響。
文中所用到的輔助程式在這裡。
一、資料處理
本文所用第三方庫如下，其中init_utils為輔助程式包含構建神經網路的函式。
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from init_utils import *通過init_utils中的load_dataset函式，可以直觀看到本文所用到的資料樣貌：
plt.rcParams['figure.figsize'] = (7.0, 4.0) plt.rcParams['image.interpolation'] = 'nearest' plt.rcParams['image.cmap'] = 'gray' train_X, train_Y, test_X, test_Y = load_dataset()
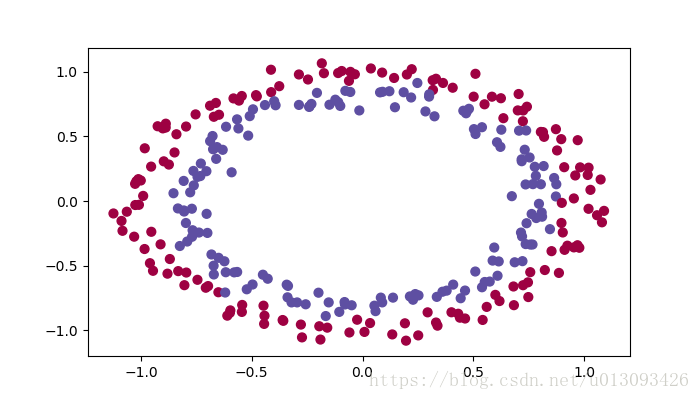二、模型搭建本文所搭建的神經網路模型與上一篇文章一致，不再贅述。
def model(X, Y, learning_rate =0.01, num_iterations = 15000, print_cost = True,intialization = "he"): grads = {} costs = [] m = X.shape[1] layers_dims = [X.shape[0],10, 5, 1] if intialization == "zeros": parameters = initialize_parameters_zeros(layers_dims) elif intialization == "random": parameters = initialize_parameters_random(layers_dims) elif intialization == "he": parameters = initialize_parameters_he(layers_dims) for i in range(0, num_iterations): a3, cache = forward_propagation(X, parameters) cost = compute_loss(a3, Y) grads = backward_propagation(X, Y, cache) parameters = update_parameters(parameters, grads, learning_rate) if print_cost and i % 100 == 0: print("cost after iterations {}:{}".format(i, cost)) costs.append(cost) plt.plot(costs) plt.xlabel("iteration (per hundreds)") plt.ylabel("cost") plt.title("Learning rate =" + str(learning_rate)) plt.show() return parameters
三、零矩陣初始化
def initialize_parameters_zeros(layers_dims): parameters = {} L = len(layers_dims) for l in range(1,L): parameters["W" + str(l)] = np.zeros((layers_dims[l],layers_dims[l-1])) parameters["b" + str(l)] = np.zeros((layers_dims[l],1)) return parameters
如果我們使用零矩陣（np.zeros()）來初始W，在之後的一系列運算中所得到的W[l]都將為0，我們來測試下這樣會得到怎麼的訓練結果。
parameters = model(train_X, train_Y, intialization = "zeros")
print("on the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print("on the test set:")
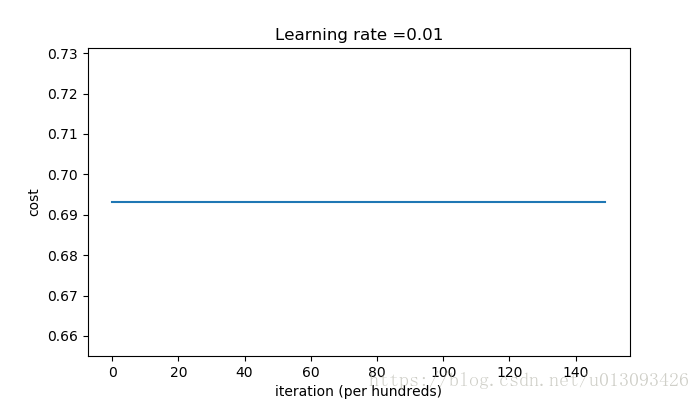
predictions_test = predict(test_X, test_Y, parameters)執行過程中我們會發現cost的計算速度很快，這也是因為使用零矩陣進行初始化的結果。
cost after iterations 0:0.6931471805599453
cost after iterations 1000:0.6931471805599453
cost after iterations 2000:0.6931471805599453
cost after iterations 3000:0.6931471805599453
cost after iterations 4000:0.6931471805599453
cost after iterations 5000:0.6931471805599453
cost after iterations 6000:0.6931471805599453
cost after iterations 7000:0.6931471805599453
cost after iterations 8000:0.6931471805599453
cost after iterations 9000:0.6931471805599453
cost after iterations 10000:0.6931471805599455
cost after iterations 11000:0.6931471805599453
cost after iterations 12000:0.6931471805599453
cost after iterations 13000:0.6931471805599453
cost after iterations 14000:0.6931471805599453
on the train set:
Accuracy: 0.5
on the test set:
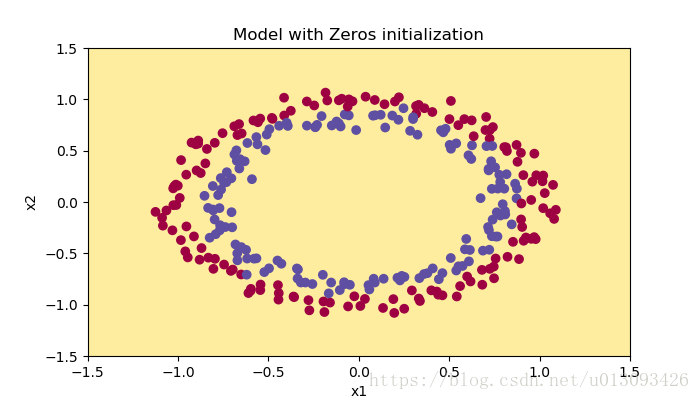
Accuracy: 0.5使用該模型對樣本進行分類，結果如下圖，把整個資料集都預測為0，劃分為一類。
有此可知：（1）b[l]可以初始化為0；（2）W[l]必須隨即初始化。
四、隨即初始化
def initialize_parameters_random(layers_dims):
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1,L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * 10
parameters["b" + str(l)] = np.zeros((layers_dims[l],1))
return parameters使用np.random.randn()函式進行初始化，且在此處測試中我們給參W[l]設定一個較大的係數，如：10。我們來看一下執行結果。
parameters = model(train_X, train_Y, intialization = "random")cost after iterations 0:inf
cost after iterations 1000:0.6239567039908781
cost after iterations 2000:0.5978043872838292
cost after iterations 3000:0.563595830364618
cost after iterations 4000:0.5500816882570866
cost after iterations 5000:0.5443417928662615
cost after iterations 6000:0.5373553777823036
cost after iterations 7000:0.4700141958024487
cost after iterations 8000:0.3976617665785177
cost after iterations 9000:0.39344405717719166
cost after iterations 10000:0.39201765232720626
cost after iterations 11000:0.38910685278803786
cost after iterations 12000:0.38612995897697244
cost after iterations 13000:0.3849735792031832
cost after iterations 14000:0.38275100578285265
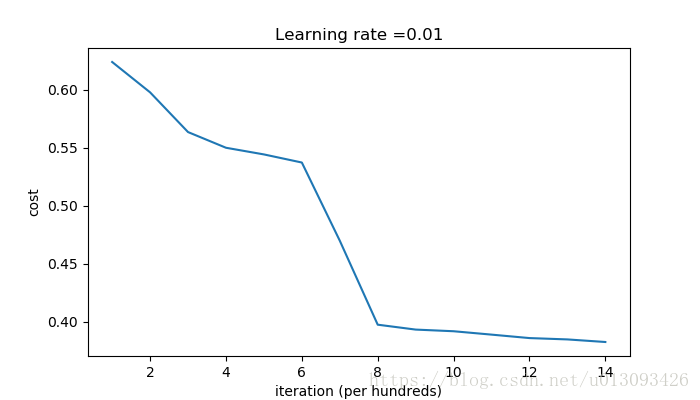
on the train set:
Accuracy: 0.83
on the test set:
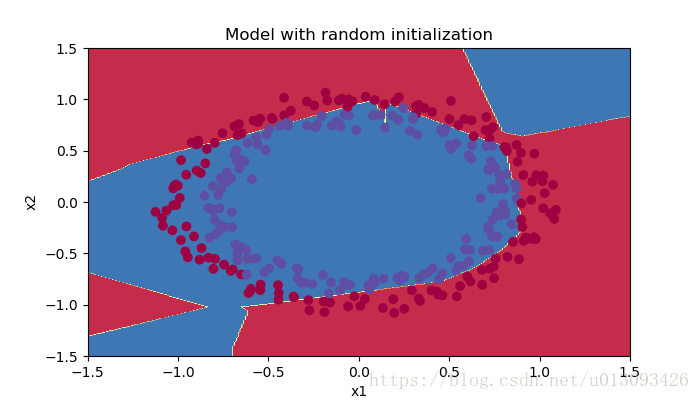
Accuracy: 0.86訓練精度明顯高很多，分類結果如下：
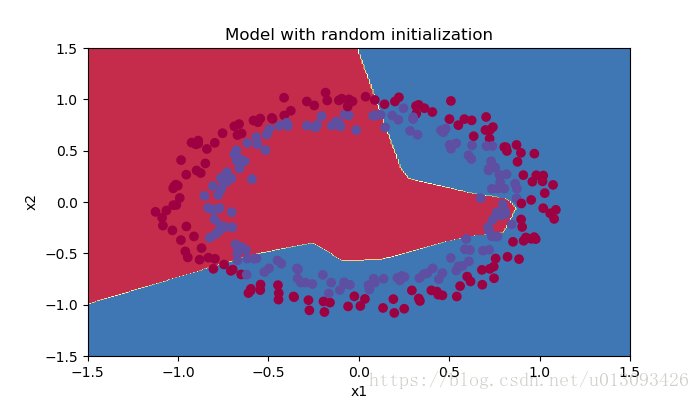
plt.title("Model with random initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
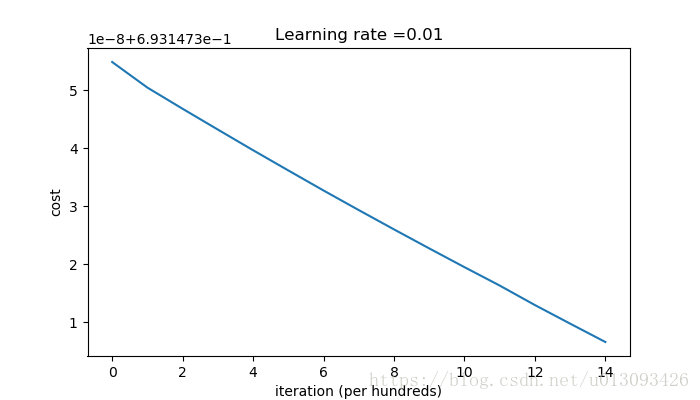
plot_decision_boundary(lambda x:predict_dec(parameters, x.T), train_X, train_Y)
從執行結果中我們可以發現，使用較大權重隨即初始化的效果雖然比零初始化效果好，但是還是有大片區域預測錯誤，那麼下面我們使用較小的權重進行實驗。
parameters["W" + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * 0.01
cost after iterations 0:0.6931473549048267
cost after iterations 1000:0.6931473504885134
cost after iterations 2000:0.6931473468317759
cost after iterations 3000:0.6931473432446151
cost after iterations 4000:0.6931473396813665
cost after iterations 5000:0.6931473361903396
cost after iterations 6000:0.6931473327310922
cost after iterations 7000:0.6931473293491259
cost after iterations 8000:0.6931473260187053
cost after iterations 9000:0.6931473227372426
cost after iterations 10000:0.6931473195009528
cost after iterations 11000:0.6931473163278133
cost after iterations 12000:0.693147312959552
cost after iterations 13000:0.6931473097541097
cost after iterations 14000:0.6931473065831708
on the train set:
Accuracy: 0.4633333333333333
on the test set:
Accuracy: 0.48
不難發現，訓練結果更差，那麼到底使用怎麼的初始權重菜才能收到較好的訓練效果呢？
五、he初始化
該方法的思路解決梯度消失或梯度爆炸問題，在W初始化時引入係數np.sqrt(2./layers_dims[l-1])。
注：對於relu啟用函式，引入係數np.sqrt(2./layers_dims[l-1])；對於tanh啟用函式，引入係數np.sqrt(1./layers_dims[l-1])
def initialize_parameters_he(layers_dims):
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for l in range(1,L):
parameters["W" + str(l)] = np.random.randn(layers_dims[l],layers_dims[l-1]) * np.sqrt(2./layers_dims[l-1])
parameters["b" + str(l)] = np.zeros((layers_dims[l],1))
return parameters我們來看一下執行結果。
parameters = model(train_X, train_Y, intialization = "he")parameters = model(train_X, train_Y, intialization = "he")
print("on the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print("on the test set:")
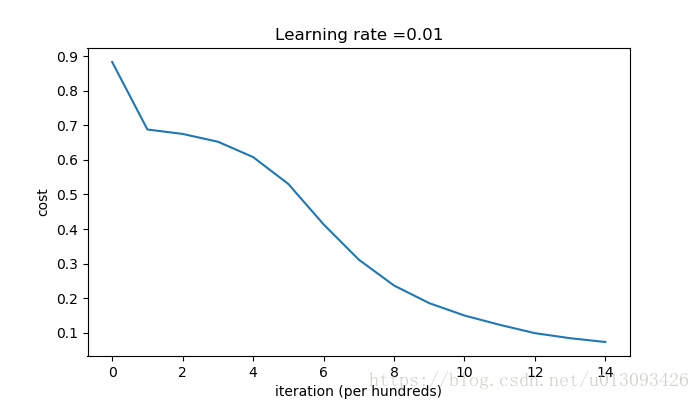
predictions_test = predict(test_X, test_Y, parameters)cost after iterations 0:0.8830537463419761
cost after iterations 1000:0.6879825919728063
cost after iterations 2000:0.6751286264523371
cost after iterations 3000:0.6526117768893807
cost after iterations 4000:0.6082958970572938
cost after iterations 5000:0.5304944491717495
cost after iterations 6000:0.4138645817071794
cost after iterations 7000:0.3117803464844441
cost after iterations 8000:0.23696215330322562
cost after iterations 9000:0.18597287209206836
cost after iterations 10000:0.15015556280371817
cost after iterations 11000:0.12325079292273552
cost after iterations 12000:0.09917746546525932
cost after iterations 13000:0.08457055954024274
cost after iterations 14000:0.07357895962677362
on the train set:
Accuracy: 0.9933333333333333
on the test set:
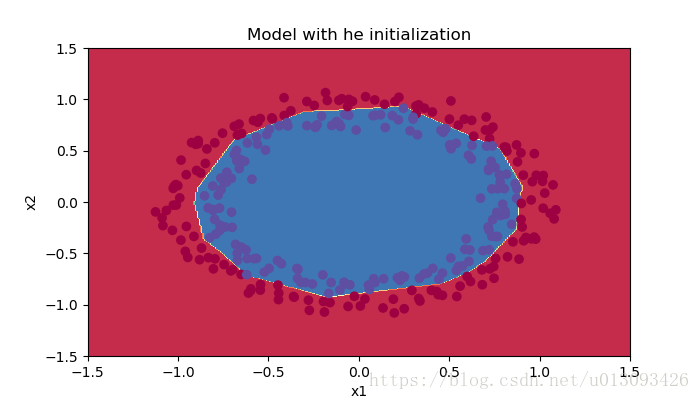
Accuracy: 0.96從訓練結果可以看出cost的下降速錄比較快，預測精度的非常高。
六、總結
1. 不同的初始化方式會導致完全不同的測試效果
2.過大、過小較大的權重進行初始化，執行效果都不理想
3.根據啟用函式的不同，選擇適當的he係數