論文筆記之Learning Convolutional Neural Networks for Graphs
本篇論文是2016ICML上的一篇論文,對於如何將cnn應用在graph上提供了一種新的思路。
架構:
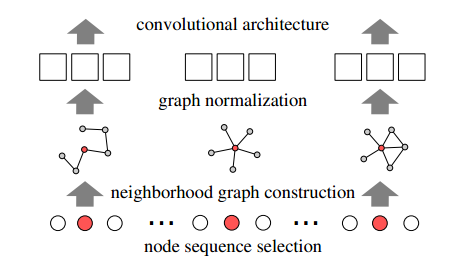
總體上講,就是用w個固定size=(k+1)的子圖來表示輸入的graph,再將這w個子圖正則化後,生成一個w(k+1)維的向量,作為傳統的cnn的輸入,進行學習。其實就是做了一個從graph到向量的對映的一個預處理過程。
演算法流程
輸入:任意一張圖
輸出:每個channel輸出w個receptive field
Step1: graph labeling(對圖的節點做標記,比如可以用節點的度做標記,做圖的劃分,也 可以叫做color refinement or vertex classification)
文中採用The Weisfeiler-Lehman algorithm做圖的劃分。由此可以得到每個節點的rank 值(為了不同的圖能夠有一個規範化的組織方式)
Step2:對labeling好的節點排序,取前w個節點,作為處理的節點序列。(這樣就可以把不 同size的graph,變成同一個size)若不足w個節點,則,在輸出中加全零的receptive field,相當於padding
Step3:採用stride=s來遍歷這w個節點。文中s=1(若s)1,為了輸出有w個receptive field, 也用step2的方式補全)
Step4:對遍歷到的每個節點v(稱作root),採用bfs的方式獲得此節點的k個1-neighborhood, 如果不k個,再遍歷1-neighborhood的1-neighborhood。直到滿足k個,或者所有的 鄰居節點都遍歷完。此節點和他的k個鄰居節點就生成了neighborhood graph。
Step5: step4就生成了w個(s=1)neighborhood graph。需要對著w個graph 進行labeling, 根據離root節點v的遠近來計算每個節點的rank,根據演算法4是離v越近,r越小。 如果每個neighborhood graph不足k個節點,用0節點補充
Step6:規範化step5得到了已經label好的graph,因為需要把它變成injective,使每個節點 的標籤唯一,採用nauty的演算法
通過這w個receptive field就能得到一個w(k+1)維的向量
