Description

求有多少種長度為 n 的序列 A，滿足以下條件：
1 ~ n 這 n 個數在序列中各出現了一次
若第 i 個數 A[i] 的值為 i，則稱 i 是穩定的。序列恰好有 m 個數是穩定的
滿足條件的序列可能很多，序列數對 10^9+7 取模。

Input

第一行一個數 T，表示有 T 組資料。
接下來 T 行，每行兩個整數 n、m。
T=500000，n≤1000000，m≤1000000

Output

輸出 T 行，每行一個數，表示求出的序列數

Sample Input

5
1 0
1 1
5 2
100 50
10000 5000

Sample Output

0
1
20
578028887
60695423

題解

錯排裸題
因為原序列中有m個數在其下標的位置上，所以有n-m個數是錯位的。
錯排遞推公式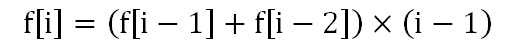
然後再乘剩下的數的組合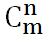就可以辣！！！

My Code

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>
#define wn 1000000007
using namespace std;
typedef long long ll;
ll f[2001412],fac[2001412
 
];
ll n,m,T;
ll inv(ll x) {
    ll y=wn-2,ans=1;
    while (y) {
        if (y&1) ans=ans*x%wn;
        x=x*x%wn;
        y>>=1;
    }
    return ans;
}
ll C(ll n,ll m){
    ll res=fac[n];
    res=(res*inv(fac[n-m]))%wn;
    res=(res*inv(fac[m]))%wn;
    return res;
}
int main() {
    scanf("%lld
 
",&T);
    f[0]=1,fac[0]=1;
    f[1]=0,fac[1]=1;
    for(ll i=2;i<=1000001;i++){
        f[i]=((f[i-1]+f[i-2])%wn*(i-1))%wn;
        fac[i]=fac[i-1]*i%wn;
    }
    while(T--){
        scanf("%lld%lld",&n,&m);    
        printf("%lld\n",(f[n-m]*C(n,m))%wn);    
    }
}