矩陣連乘最少次數
一.問題描敘
給定n個矩陣{A1,A2,……,An},其中Ai與Ai+1是可乘的,i=1,2,……,n-1。
例如:
計算三個矩陣連乘{A1,A2,A3};維數分別為10*100 , 100*5 , 5*50
按此順序計算需要的次數((A1*A2)*A3):10X100X5+10X5X50=7500次
按此順序計算需要的次數(A1*(A2*A3)):10X5X50+10X100X50=75000次
所以要解決的問題是:如何確定矩陣連乘積A1A2,……An的計算次序,使得按此計算次序計算矩陣連乘積需要的數乘次數達到最小化。
二.問題分析
由於矩陣乘法滿足結合律,所以計算矩陣連乘的連乘積可以與許多不同的計算計算次序,這種計算次序可以用加括號的方式來確定。若一個矩陣連乘積的計算次序完全確定,也就是說連乘積已完全加括號,那麼可以依此次序反覆呼叫2個矩陣相乘的標準演算法計算出矩陣連乘積。
完全加括號的矩陣連乘積可遞迴地定義為:
(1).單個矩陣是完全加括號的;
(2).矩陣連乘積A是完全加括號的,則A可以表示為2個完全加括號的矩陣連乘積B和C的乘積並加括號,及A=(BC);
舉個例子,矩陣連乘積A1A2A3A4A5,可以有5種不同的完全加括號方式:
(A1(A2(A3A4))),(A1((A2A3)A4)),((A1A2)(A3A4)),((A1(A2A3))A4),(((A1A2)A3)A4)
每一種完全加括號的方式對應一種矩陣連乘積的計算次序,而矩陣連乘積的計算次序與其計算量有密切的關係,即與矩陣的行和列有關。
補充一下數學知識,矩陣A與矩陣B可乘的條件為矩陣A的列數等於矩陣B的行數,例如,若A是一個p*q的矩陣,B是一個q*r的矩陣,則其乘積C=AB是一個p*r的矩陣。
三.動態規劃解決矩陣連乘積的最優計算次序問題
或許你對動態規劃有點陌生,那簡單的講講什麼叫動態規劃吧。
動態規劃演算法與分治法類似,其基本思想也就是將待求解的問題分解成若干個子問題,先求解子問題,然後從這些子問題的解得到原問題的解,簡單概括為自頂向下分解,自底向上求解。與分治法不同的是,適合於用動態規劃法求解的問題,經分解得到的子問題往往不是相互獨立的,換句話說,就是前面解決過的子問題,在後面的子問題中又碰到了前面解決過的子問題,子問題之間是有聯絡的。如果用分治法,有些同樣的子問題會被重複計算幾次,這樣就很浪費時間了。所以動態規劃是為了解決分治法的弊端而提出的,動態規劃的基本思想就是,用一個表來記錄所有已經解決過的子問題的答案,不管該子問題在以後是否會被用到,只要它被計算過,就將其結果填入表中,以後碰到同樣的子問題,就可以從表中直接呼叫該子問題的答案,而不需要再計算一次。具體的動態規劃的演算法多種多樣,但他們都具有相同的填表式。
順便說一下動態規劃的適用場合,一般適用於解最優化問題,例如矩陣連乘問題、最長公共子序列、揹包問題等等,通常動態規劃的設計有4個步驟,結合矩陣連乘分析:
(1).找出最優解的性質,並刻畫其結構特徵
這是設計動態規劃演算法的第一步,我們可以將矩陣連乘積AiAi+1……Aj記為A[i:j]。問題就是計算A[1:n]的最優計算次序。設這個計算次序在矩陣Ak和Ak+1之間將矩陣鏈斷開,1<=k<n,使其完全加括號方式為((A1……Ak)(AK+1……An)),這樣就將原問題分解為兩個子問題,,按此計算次序,計算A[1:n]的計算量就等於計算A[1:k]的計算量加上A[k+1:n]的計算量,再加上A[1:k]和A[k+1:n]相乘的計算量。計算A[1:n]的最優次序包含了計算A[1:k]和A[k+1:n]這兩個子問題的最優計算次序,以此類推,將A[1:k]和A[k+1:n]遞迴的分解下去,求出每個子問題的最優解,子問題的最優解相乘便得到原問題的最優解。
(2).遞迴地定義最優值
這是動態規劃的第二步,對於矩陣連乘積的最優計算次序的問題,設計算A[i:j],1<=i<=j<=n,所需要的最小數乘次數為m[i][j],則原問題的最優值為m[1][n]。
當i=j時,A[i:j]=Ai為單一的矩陣,則無需計算,所以m[i][j]=0,i=j=1,2,……,n。即對應的二維表對角線上的值全為0。
當i<j時,這就需要用步驟(1)的最優子結構性質來計算m[i][j]。若計算A[i:j]的最優次序在Ak和Ak+1之間斷開,i<=k<j,則m[i][j]=m[i][k]+m[k+1][j]+pi-1*pk*pj,k的位置只有j-i種可能,即k屬於集合{i,i+1,……,j-1},所以k是這j-i個位置中使計算量達到最小的那個位置。
所以m[i][j]可以遞迴地定義為 m[i][j]={ 0 i=j
min{m[i][k]+m[k+1][j]+pi-1*pk*pj } i<j ,i<=k<j }
將對應於m[i][j]的斷開位置k記為s[i][j],在計算出最優值m[i][j]後,可遞迴地由s[i][j]構造出相應的最優解
(3).以自底向上的方式計算出最優值
動態規劃的一大好處是,在計算的過程中,將已解決的子問題答案儲存起來,每個子問題只計算一次,而後面的子問題需要用到前面已經解決的子問題,就可以從表中簡單差出來,從而避免了大量的重複計算
動態規劃演算法 這裡的p[],m[][],s[][]都為全域性變數
以A1A2A3A4A5A6為例,其中各矩陣的維數分別為:
A1:30*35, A2:35*15, A3:15*5, A4:5*10, A5:10*20, A6:20*25
動態規劃演算法matrixchain計算m[ i ][ j ]先後次序如圖所示,計算結果為m[ i ][ j ]和s[ i ][ j ],其中第0行和第0列沒有使用。
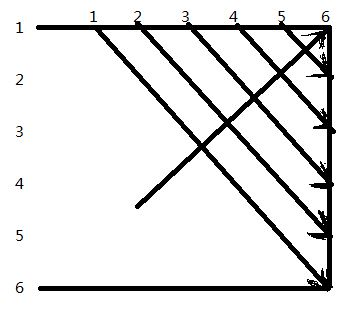
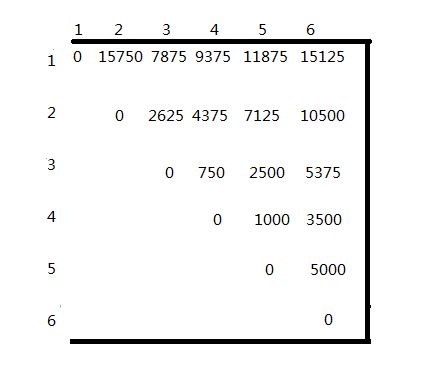
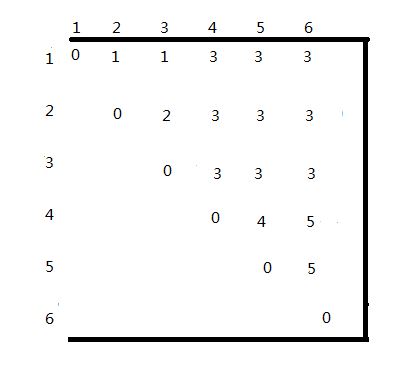
計算次序 m[i][j] s[i][j]
例如,在計算m[2][5]時,依遞迴式有
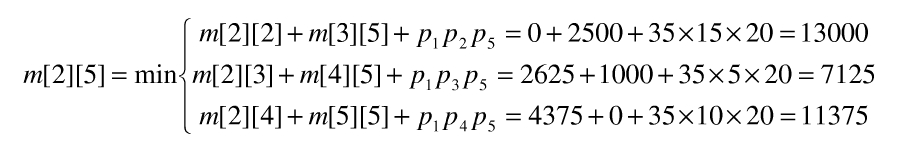
所以m[2][5] = 7125,且k=3,因此,s[2][5]=3。
(4).根據計算最優值時得到的資訊(及存放最優值的表格),構造最優解
動態規劃演算法的第四布是構造問題的最優解。演算法matrixchain只是計算出了最優值,並未給出最優解。也就是說,通過matrixchain的計算,只是到最少數乘次數,還不知道具體應按什麼次序來做矩陣乘法才能達到最少的數乘次數。
****************************************************************************************************************************模板:
#include <stdio.h>
#include <stdlib.h>
#define MAX 50
#define inf 99999999
int p[MAX+1]; //儲存各個矩陣的列數以及第一個矩陣的行數(作為第0個矩陣的列數)
int m[MAX][MAX]; //m[i][j]儲存子問題的最優解
int s[MAX][MAX]; //s[i][j]儲存子問題的最佳分割點
int n; //矩陣個數
void matrix()
{
int i,j,k;
for(i=0;i<n;i++)
m[i][i]=0; //最小子問題僅含有一個矩陣 ,對角線全為0
for(i=2;i<=n;i++)
for(j=0;j<n-i+1;j++)
{
m[j][j+i-1]=inf;
for(k=0;k<i-1;k++)
{ //k代表分割點
if(m[j][j+i-1]>m[j][j+k]+m[j+k+1][j+i-1]+p[j]*p[j+k+1]*p[j+i])
{
m[j][j+i-1]=m[j][j+k]+m[j+k+1][j+i-1]+p[j]*p[j+k+1]*p[j+i];
s[j][j+i-1]=k; //記錄分割點
}
}
}
}
void printmatrix(int leftindex,int rightindex)//遞迴列印輸出
{
if(leftindex==rightindex)
printf("A%d",leftindex);
else{
printf("(");
printmatrix(leftindex,leftindex+s[leftindex][rightindex]);
printmatrix(leftindex+s[leftindex][rightindex]+1,rightindex);
printf(")");
}
}
int main()
{
int i;
printf("請輸入矩陣相乘的矩陣個數");
scanf("%d",&n);
printf("請依次輸入矩陣的行和烈(如A*B,A=20*30,B=30*40,即輸入20 30 40)\n") ;
for(i=0;i<n+1;i++)
{
scanf("%d",&p[i]);
}
matrix();
printf("矩陣連乘最小次數\t%d\n",m[0][n-1]);
printmatrix(0,n-1);
printf("\n");
return 0;
}