2. 程式人生 > >演算法導論--動態順序統計與區間樹

演算法導論--動態順序統計與區間樹

阿新 • • 發佈：2019-02-12

通過在基礎的資料結構中新增一些附加資訊，來擴張一種標準的資料結構，然後編寫新的操作來支援所需要的應用。下面是介紹在紅黑樹的基礎上擴張的資料結構。

1.動態順序統計

動態順序統計可以在O(lgn)時間內確定任何的順序統計量(即在n個元素的集合中，能在O(lgn)的時間內確定第i小的元素)，同時也可以在O(lgn)的時間內計算一個元素的秩(即它在中序遍歷下的位置順序)。

1 新增附加資訊

結點x中加入x.size , size的大小為以x為根的子樹（包含x本身）的內結數，即子樹的大小。我們定義哨兵的size為0，如下圖：

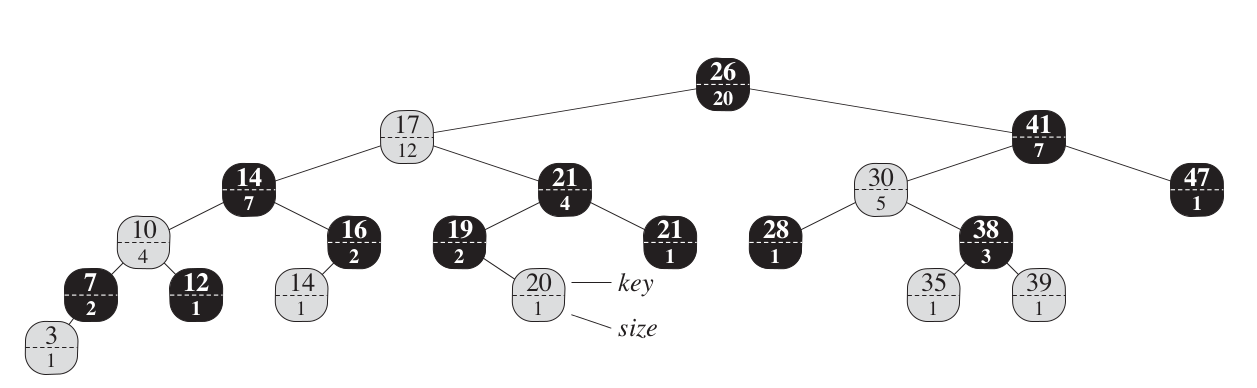
結點內，虛線上方為關鍵字key，下方為結點的size。
可以看出： x.size = x.left.size + x.right.size +1；

enum colors{red,black};//列舉型別
typedef struct Node
{
   struct Node * p;
   struct Node *left;
   struct Node *right;
   int key;             
   enum  colors color;  //顏色屬性
   int size;           //新新增的屬性size
}Node;

2 修改基本操作

插入操作：
為了對子樹規模的維護，需要在不影響插入和刪除操作的漸進執行時間的前提下，修改基本的操作。
第一階段：新節點的插入過程中，需要對從根到將要插入的位置過程中遍歷的結點的size加1；
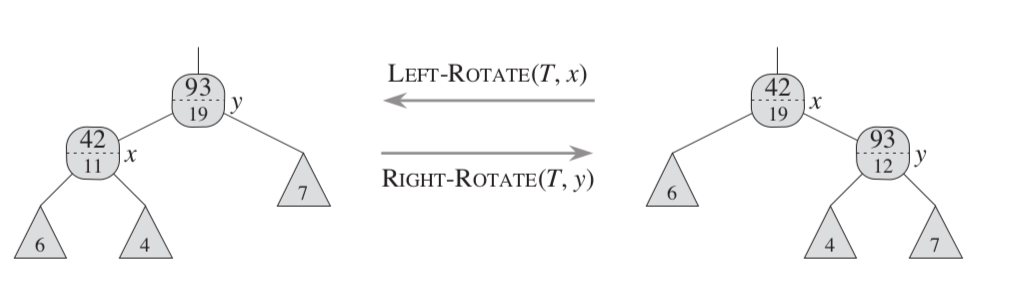
第二階段：維護紅黑樹的左旋和右旋函式需要在最後新增以下語句： 

 /*左旋*/
    y.size = x.size;
    x.size = x.left.size + x.right.size +1;
 /*右旋*/
    x.size = y.size;
    y.size = y.left.size + y.right.size +1;

刪除操作：
第一階段：如果要刪除的結點z少於兩個孩子，則從z到根T的過程遍歷的結點size減1；如果要刪除的結點z多於兩個孩子，則從z的後繼y處向上到T的過程中，遍歷的結點size減1；
第二階段：
也是同樣在左右旋過程中，新增以上的語句；
插入操作和刪除操作執行時間都是O(lgn).

3 設計新的操作

1.給定秩的元素的檢索
呼叫函式OS_Select(Node * x,int i)檢索出在以x為根的子樹中，第i小的關鍵字的結點。執行時間為O(lgn);

Node * OS_Select(Node *x,int i)
{
    int r =x->left->size+1;           //計算以結點x為根的子樹中順序統計量r
    if (i == r)
        return x;   
    else if (i < r)                
        return OS_Select(x->left,i);  //在x的左子樹裡繼續遞迴查詢
    else
        return OS_Select(x->right,i-r);//在x的右子樹裡繼續遞迴查詢
}

2.確定一個元素的秩
給定指向T中，結點x的指標，過程OS_Rank返回對T中序遍歷對應的線性序中x的位置；執行時間為O(lgn)

int OS_Rank(Node *T,Node * x)
{
    int r =x->left->size+1;  //計算以結點x為根的子樹中順序統計量r
    Node * y =x;
    while(y != T)                 //疊加到root根節點位置
    {
        if (y == y->p->right)          //父節點的右子樹輸出在左子樹和根之後，順序統計量疊加
        {
            r=r+y->p->left->size+1;
        }
        y = y->p;                      //若屬於左子樹，直接跳向上層
    }
    return r;
}

4 完整程式碼

/*        
CSDN 勿在浮砂築高臺
http://blog.csdn.net/luoshixian099
演算法導論--順序統計量
2015年5月20日
*/
#include <STDIO.H> 
#include <STDLIB.H>
enum colors{red,black};//列舉型別
typedef struct Node
{
   struct Node * p;
   struct Node *left;
   struct Node *right;
   int key;
   enum  colors color;
   int size;                       //新增附加資訊size
}Node;
Node *T_NIL=NULL;                 //建立全部變數 T_NIL

Node * Tree_Minimum(Node * T)     //找最小結點
{
    while(T->left != T_NIL)
        T=T->left;
    return T;
}
void Inorder_Tree_Walk(Node * T)  //中序遍歷樹T,輸出
{
    if ( T != T_NIL)
    {
        Inorder_Tree_Walk(T->left);   //遞迴其左孩子
        printf("%d",T->key);        //輸出根的關鍵字
        if (T->color == 0)
        {
            printf("-R");
        }
        else
        {
            printf("-B");
        }
        printf("-(%d)  ",T->size);
        Inorder_Tree_Walk(T->right);  //遞迴其右孩子
    }
}
void Pre_Tree_Walk(Node * T)  //
{
    if ( T != T_NIL)
    {     
        printf("%d    ",T->key);          //輸出根的關鍵字
        Pre_Tree_Walk(T->left);   //遞迴其左孩子      
        Pre_Tree_Walk(T->right);  //遞迴其右孩子

    }
}

void Left_Rotate(Node **T,Node * x)   //左旋
{
   Node *y=x->right;

   x->right =y->left;
   if (y->left != T_NIL)
       y->left->p=x;
   y->p=x->p;
   if(x->p==T_NIL)
      *T=y;
   else if (x == x->p->left)
      x->p->left = y;
   else
      x->p->right = y;
   y->left = x;
   x->p=y;

   y->size = x->size;                         //新增語句維護size
   x->size = x->left->size+x->right->size+1;
}
void Right_Rotate(Node **T,Node * y)   //右旋
{
    Node *x=y->left;

    y->left =x->right;
    if (x->right != T_NIL)
        x->right->p=y;
    x->p=y->p;
    if(y->p==T_NIL)
        *T=x;
    else if (y == y->p->left)
        y->p->left = x;
    else  
        y->p->right = x;
    x->right = y;
    y->p=x;

   x->size = y->size;                     //新增語句維護size
   y->size = y->left->size+y->right->size+1;
}
Node* RB_Insert_Fixup(Node *T,Node *z)
{
    Node * y=NULL;
   while( z->p->color == red)       //違反了性質4，迭代進行修正
   {
      if (z->p == z->p->p->left)
      {
          y = z->p->p->right;
          if ( y->color == red)    // case 1 叔結點為紅色
          {
             z->p->color = black;    //父節點塗黑
             y->color = black;       //叔結點塗黑
             z->p->p->color = red;   //祖結點塗紅
             z = z->p->p;            //向上迭代，更新z的位置
          }
          else if ( z == z->p->right) //case 2 叔結點為黑色且z為雙親的右孩子
          {
             z = z->p;
             Left_Rotate(&T,z);
             z->p->color = black;    //case2 已轉為 case3 繼續處理
             z->p->p->color = red;
             Right_Rotate(&T,z->p->p);// while迴圈終止
          }
          else                      // case 3 叔結點為黑色且z為雙親的左孩子 
          {
             z->p->color = black;
             z->p->p->color = red;
             Right_Rotate(&T,z->p->p);//   while迴圈終止 
          }
      }

      else                      //對稱處理
      {

          y = z->p->p->left;
          if ( y->color == red)    // case 1 叔結點為紅色
          {
              z->p->color = black;
              y->color = black;
              z->p->p->color = red;
              z = z->p->p;
          }

          else if ( z == z->p->left) //case 2 叔結點為黑色且z為雙親的右孩子
          {
              z = z->p;
              Right_Rotate(&T,z);
              z->p->color = black;
              z->p->p->color = red;
              Left_Rotate(&T,z->p->p);// 
          }
          else                      // case 3
          {
              z->p->color = black;
              z->p->p->color = red;
              Left_Rotate(&T,z->p->p); 
          }

      }  
   }

   T->color = black;          //保證不會違反性質2，對根節點塗黑
   return T;
}
Node *RB_Insert(Node *Root,Node * z)   //紅黑樹插入,返回樹的根
{
    Node * y=T_NIL;
    Node * x=Root;
    while( x != T_NIL)                 //找到結點z要插入的位置    
    {
        x->size+=1;                    //插入過程中，遍歷的結點size加1

        y=x;
        if (z->key < x->key)
            x = x->left;
        else
            x = x->right;
    }
    z->p = y;
    if ( y == T_NIL)    //插入第一個結點作為根節點的情況  
        Root = z;
    else if (z->key < y->key)
        y->left = z;
    else    
        y->right = z;

    Root = RB_Insert_Fixup(Root,z);    //插入完畢後，對紅黑樹的顏色進行修正
    return Root; 
}
Node * Establish(int *A,int len)   //建立紅黑樹
{
   Node * T,*node;
   int i=0;
   node=NULL;
   T_NIL=(Node *)malloc(sizeof(Node));  //建立T_NIL結點
   T_NIL->p=NULL;
   T_NIL->left=NULL;
   T_NIL->right=NULL;
   T_NIL->key=-1;
   T_NIL->color=black;
   T_NIL->size=0;
   T=T_NIL;
   for (i=0;i<len;i++)
   {
       node =(Node *)malloc(sizeof(Node));
       node->p =T_NIL;
       node->left=T_NIL;
       node->right=T_NIL;
       node->key=A[i];
       node->color=red;
       node->size=1;
       T=RB_Insert(T,node);
   }
   return T;
}

void RB_Transplant(Node **T,Node * u,Node * v)  //結點替代函式
{
  if (u->p == T_NIL)
      *T = v;
  else if (u == u->p->left)
     u->p->left = v;
  else
     u->p->right = v;
  v->p = u->p;               //此處賦值無條件，v如果是T_NIL也要進行賦值
}
void RB_Delete_Fixup(Node * T,Node * x)
{
    Node *w=NULL;
  while( x != T && x->color == black)      //迴圈迭代處理
  {
      if ( x == x->p->left )
      {
        w = x->p->right;
        if (w->color == red)             // case 1 ------> case 2 , case 3 ,case 4 
        {
            w->color = black;
            x->p->color =red;
            Left_Rotate(&T,x->p);
            w = x->p->right;
        }
        if ( w->left->color == black && w->right->color == black ) //case 2 ------>go on / stop
        {
            w->color = red;
            x = x->p;
        }
        else if ( w->right->color == black)   // case 3 ---->case 4---->stop
        {
           w->left->color = black;
           w->color =red ;
           Right_Rotate(&T,w);

           w = x->p->right ;                   //轉成case 4處理 
           w->color = x->p->color;
           x->p->color = black;
           w->right->color = black;
           Left_Rotate(&T,x->p);
           x = T;
        }
        else                               // case 4 ------------------->stop
        {
            w->color = x->p->color;
            x->p->color = black;
            w->right->color = black;
            Left_Rotate(&T,x->p);
            x = T;
        }
      }
      else
      {
          w = x->p->left;
          if (w->color == red)                // case 1 ------> case 2 , case 3 ,case 4 
          {
              w->color = black;
              x->p->color =red;
              Right_Rotate(&T,x->p);
              w = x->p->left;
          }
          if ( w->right->color == black && w->left->color == black ) //case 2 ------>go on/stop
          {
              w->color = red;
              x = x->p;
          }
          else if ( w->left->color == black)      // case 3 -----> case 4----->stop
          {
              w->right->color = black;
              w->color =red ;
              Left_Rotate(&T,w);

              w = x->p->left ;                    //轉成case 4處理
              w->color = x->p->color;
              x->p->color = black;
              w->left->color = black;
              Right_Rotate(&T,x->p);
              x = T;
          }
          else                                  // case 4 -------------->stop
          {
              w->color = x->p->color;
              x->p->color = black;
              w->left->color = black;
              Right_Rotate(&T,x->p);
              x = T;
        }
      }
  }

  x->color = black;                       //可能由case2退出，那把x塗黑即可，見分析！也可能有case4退出，把根節點塗黑
}
Node * RB_Delete(Node *T ,Node *z)
{

    Node * x =NULL;
    Node * y =z;
    Node *temp=y->p;
    enum colors y_original_color = y->color;   //記錄下刪除前z的顏色
    if ( z->left == T_NIL)                     //左子樹不存在的情況  
    {
        x = z->right;
        RB_Transplant(&T,z,z->right);
    }
    else if ( z->right == T_NIL)              //右子樹不存在
    {
       x = z->left;
       RB_Transplant(&T,z,z->left);
    }
    else                                     //左右都存在的情況
    {
       y = Tree_Minimum(z->right);            //找到後繼y
       temp=y->p;   
       y_original_color = y->color;           //記錄下y轉移前的顏色
       x = y->right;
       if ( y->p == z)                       //如果y是z的子結點
       {
         x->p = y;
       }
       else
       {
           RB_Transplant(&T,y,y->right);    //如果y不是z的子結點，用y的右子樹代替y的位置
           y->right = z->right;
           y->right->p = y;
       }
       RB_Transplant(&T,z,y);           //y替代z的位置 ，不論y是不是T_NIL   
       y->left = z->left;
       y->left->p = y;
       y->color = z->color;             //把y的顏色改成z的顏色

       y->size =y->left->size+y->right->size+1;
    }

     while(temp != T_NIL)             //從刪除的位置或後繼的位置向上遍歷size--,直到根節點為止
        {
            temp->size--;
            temp = temp->p;
        }



    if ( y_original_color == black)   //判斷y的顏色，若為黑色，需要修復
        RB_Delete_Fixup(T,x);
    return T;
}

Node * Tree_Search(Node *T ,int k)  //尋找數k是否在樹中，且返回數k的地址
{   

    while(T !=T_NIL && T->key != k)
    {
        if ( k < T->key)
            T=T->left;
        else
            T=T->right;
    }

    if ( T == T_NIL)
    {     
        return NULL;
    }

    else 
    {
        return T;
    }

}
Node * OS_Select(Node *x,int i)        //確定以x為根節點的子樹，第i小的關鍵字
{
    int r =x->left->size+1;
    if (i == r)
        return x;   
    else if (i < r)
        return OS_Select(x->left,i);
    else
        return OS_Select(x->right,i-r);
}
int OS_Rank(Node *T,Node * x)         //確定x在樹T中序遍歷中的位置順序
{
    int r =x->left->size+1;
    Node * y =x;
    while(y != T)
    {
        if (y == y->p->right)
        {
            r=r+y->p->left->size+1;
        }
        y = y->p;
    }
    return r;
}
void main()
{
    int A[]={2,5,1,6,3,8,4,9,7};

    int length = sizeof(A)/sizeof(A[0]); //陣列A的長度
    Node *T =Establish(A,length);        //建立紅黑樹，返回根節點T

    printf("中序遍歷：\n");
    Inorder_Tree_Walk(T);printf("\n");   //中序遍歷輸出

    printf("先序遍歷：\n");              //先序遍歷輸出
    Pre_Tree_Walk(T);printf("\n");

    printf("__%d__\n",OS_Select(T,5)->key);
    printf("--%d--\n",OS_Rank(T,Tree_Search(T,3)));

    printf("-----------刪除操作後-------------\n");

    T=RB_Delete(T,Tree_Search(T,2));
    T=RB_Delete(T,Tree_Search(T,5));
    T=RB_Delete(T,Tree_Search(T,7));
    T=RB_Delete(T,Tree_Search(T,4));
    printf("中序遍歷：\n");
    Inorder_Tree_Walk(T);
    printf("\n");

    printf("先序遍歷：\n");
    Pre_Tree_Walk(T);

    printf("\n");
}

2.區間樹

區間樹是通過擴張紅黑樹來構成由區間構成的動態集合。結點的屬性由一個關鍵字key變成了一個區間。

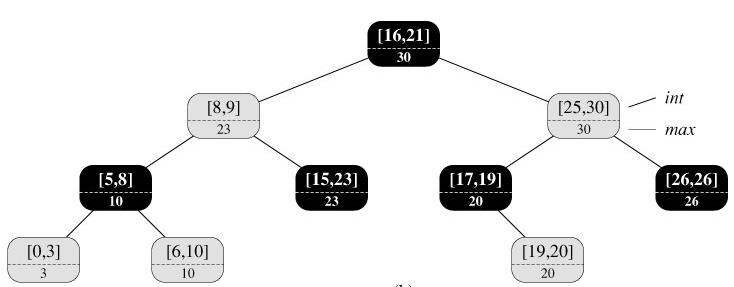
1.新增附加資訊

新增區間資訊INT,INT結構包含區間的左右端點。還包含Max屬性，它是以自身為根的子樹中所有的區間的端點最大值。（上圖中虛線下方）

enum colors{red,black};//列舉型別
struct Interval //區間
{
    int low;
    int high;
};
typedef struct Node
{
   struct Node * p;
   struct Node *left;
   struct Node *right;
   enum  colors color;
   //新增的屬性
   struct Interval INT;   //儲存結點區間資訊                   
   int  Max;              //以結點為根的所有區間端點的最大值      
}Node;

2.修改基本操作

修改紅黑樹的插入和刪除操作維新增的資訊，都能保證在O(lgn)的時間內完成；
1.插入操作：
第一步：由於區間樹採用區間左端點作為關鍵字進行插入，遍歷時通過比較INT.low的方式插入；插入前令Max=high，插入時從根節點開始遍歷到要插入的位置，把遍歷的結點的Max與新新增的結點z的Max進行比較，如果z.Max>x.Max ,更新結點的x.Max=z.Max

Node *Interval_Insert(Node *Root,Node * z)   //紅黑樹插入,返回樹的根
{
    Node * y=T_NIL;
    Node * x=Root;
    while( x != T_NIL)                 //找到結點z要插入的位置    
    {
        if ( z->Max > x->Max)     //比較新插入的結點z與結點x的Max大小；
        {
            x->Max = z->Max;
        }
        y=x;
        if (z->INT.low < x->INT.low)
            x = x->left;
        else
            x = x->right;
    }
    z->p = y;
    if ( y == T_NIL)    //插入第一個結點作為根節點的情況  
        Root = z;
    else if (z->INT.low < y->INT.low)
        y->left = z;
    else    
        y->right = z;

    Root = Interval_Insert_Fixup(Root,z);    //插入完畢後，對紅黑樹的顏色進行修正
    return Root; 
}

第二步：由於左旋右旋會破壞區間的性質，在函式程式碼後新增更新資訊

void Left_Rotate(Node **T,Node * x)   //左旋
{
   Node *y=x->right;

   x->right =y->left;
   if (y->left != T_NIL)
       y->left->p=x;
   y->p=x->p;
   if(x->p==T_NIL)
      *T=y;
   else if (x == x->p->left)
      x->p->left = y;
   else
      x->p->right = y;
   y->left = x;
   x->p=y;

  y->Max = x->Max;                         //新增語句維護Max
  x->Max = GetMax(x->left->Max,x->right->Max,x->INT.high);
}
void Right_Rotate(Node **T,Node * y)   //右旋
{
    Node *x=y->left;

    y->left =x->right;
    if (x->right != T_NIL)
        x->right->p=y;
    x->p=y->p;
    if(y->p==T_NIL)
        *T=x;
    else if (y == y->p->left)
        y->p->left = x;
    else  
        y->p->right = x;
    x->right = y;
    y->p=x;

  x->Max = y->Max;                         //新增語句維護Max
  y->Max = GetMax(y->left->Max,y->right->Max,y->INT.high);
}

2.刪除操作

第一步：被刪除的結點z可能會影響整個區間樹的性質，如果結點z少於兩個孩子，則沿著z上升到根節點為止，對樹重新更新維護；如果有兩個孩子則從後繼出發，進行維護；

while( temp != T_NIL )             //從要刪除的結點或其後繼開始向上修復區間樹
    {       
            temp->Max = GetMax(temp->left->Max,temp->right->Max,temp->INT.high);
            temp = temp->p;     //每次一層，至多lgn層
    }

第二步：同上，也是在左旋右旋函式後新增程式碼。

3.設計新的操作

判斷給定的一個區間i位於區間樹的哪個位置。區間之間的關係：

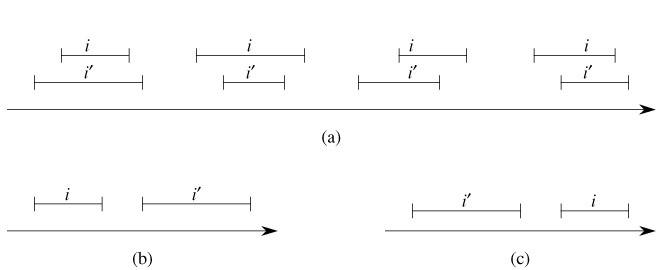
a重疊的情況；b、c不重疊的情況
不重疊的情況用程式碼表示為

x->INT.high < i->low
x->INT.low  > i->high

如果存在區間與i重疊則返回結點的位置，否則返回T_NIL

Node * Interval_Search(Node *T ,struct Interval *i)  //尋找數k是否在樹中，且返回數k的地址
{   
    Node * x = T;
    while(x != T_NIL && ((x->INT.high < i->low)||(x->INT.low > i->high)))  //不重疊
    {
        if (x->left != T_NIL && x->left->Max >= i->low)  //在其左子樹中搜索
        {
            x = x->left;
        }
        else
        {
            x = x->right;
        }
    }

    return x;
}

每次迭代都是一層，至多lgn層；所以耗時O(lgn)的時間

4.完整程式碼

/*        
CSDN 勿在浮砂築高臺
http://blog.csdn.net/luoshixian099
演算法導論--區間樹
2015年5月20日
*/
#include <STDIO.H> 
#include <STDLIB.H>
enum colors{red,black};//列舉型別
struct Interval //區間
{
    int low;
    int high;
};
typedef struct Node
{
   struct Node * p;
   struct Node *left;
   struct Node *right;
   enum  colors color;
   //新增的屬性
   struct Interval INT;   //儲存結點區間資訊                   
   int  Max;              //以結點為根的所有區間端點的最大值      
}Node;
Node *T_NIL=NULL;                 //建立全部變數 T_NIL

int GetMax(int a,int b,int c)    //返回a,b,c最大值
{
    return a>b?(a>c?a:c):(b>c?b:c);
}
Node * Tree_Minimum(Node * T)     //找最小結點
{
    while(T->left != T_NIL)
        T=T->left;
    return T;
}
void Inorder_Tree_Walk(Node * T)  //中序遍歷樹T,輸出
{
    if ( T != T_NIL)
    {
        Inorder_Tree_Walk(T->left);   //遞迴其左孩子
        printf("%d",T->INT.low);        //輸出根的關鍵字
        if (T->color == 0)
        {
            printf("-R(%d)  ",T->Max);
        }
        else
        {
            printf("-B(%d)   ",T->Max);
        }
        Inorder_Tree_Walk(T->right);  //遞迴其右孩子
    }
}
void Pre_Tree_Walk(Node * T)  //
{
    if ( T != T_NIL)
    {     
        printf("%d    ",T->INT.low);          //輸出根的關鍵字
        Pre_Tree_Walk(T->left);   //遞迴其左孩子      
        Pre_Tree_Walk(T->right);  //遞迴其右孩子

    }
}

void Left_Rotate(Node **T,Node * x)   //左旋
{
   Node *y=x->right;

   x->right =y->left;
   if (y->left != T_NIL)
       y->left->p=x;
   y->p=x->p;
   if(x->p==T_NIL)
      *T=y;
   else if (x == x->p->left)
      x->p->left = y;
   else
      x->p->right = y;
   y->left = x;
   x->p=y;

  y->Max = x->Max;                         //新增語句維護Max
  x->Max = GetMax(x->left->Max,x->right->Max,x->INT.high);
}
void Right_Rotate(Node **T,Node * y)   //右旋
{
    Node *x=y->left;

    y->left =x->right;
    if (x->right != T_NIL)
        x->right->p=y;
    x->p=y->p;
    if(y->p==T_NIL)
        *T=x;
    else if (y == y->p->left)
        y->p->left = x;
    else  
        y->p->right = x;
    x->right = y;
    y->p=x;

  x->Max = y->Max;                         //新增語句維護Max
  y->Max = GetMax(y->left->Max,y->right->Max,y->INT.high);
}
Node* Interval_Insert_Fixup(Node *T,Node *z)
{
    Node * y=NULL;
   while( z->p->color == red)       //違反了性質4，迭代進行修正
   {
      if (z->p == z->p->p->left)
      {
          y = z->p->p->right;
          if ( y->color == red)    // case 1 叔結點為紅色
          {
             z->p->color = black;    //父節點塗黑
             y->color = black;       //叔結點塗黑
             z->p->p->color = red;   //祖結點塗紅
             z = z->p->p;            //向上迭代，更新z的位置
          }
          else if ( z == z->p->right) //case 2 叔結點為黑色且z為雙親的右孩子
          {
             z = z->p;
             Left_Rotate(&T,z);
             z->p->color = black;    //case2 已轉為 case3 繼續處理
             z->p->p->color = red;
             Right_Rotate(&T,z->p->p);// while迴圈終止
          }
          else                      // case 3 叔結點為黑色且z為雙親的左孩子 
          {
             z->p->color = black;
             z->p->p->color = red;
             Right_Rotate(&T,z->p->p);//   while迴圈終止 
          }
      }

      else                      //對稱處理
      {

          y = z->p->p->left;
          if ( y->color == red)    // case 1 叔結點為紅色
          {
              z->p->color = black;
              y->color = black;
              z->p->p->color = red;
              z = z->p->p;
          }

          else if ( z == z->p->left) //case 2 叔結點為黑色且z為雙親的右孩子
          {
              z = z->p;
              Right_Rotate(&T,z);
              z->p->color = black;
              z->p->p->color = red;
              Left_Rotate(&T,z->p->p);// 
          }
          else                      // case 3
          {
              z->p->color = black;
              z->p->p->color = red;
              Left_Rotate(&T,z->p->p); 
          }

      }  
   }

   T->color = black;          //保證不會違反性質2，對根節點塗黑
   return T;
}
Node *Interval_Insert(Node *Root,Node * z)   //紅黑樹插入,返回樹的根
{
    Node * y=T_NIL;
    Node * x=Root;
    while( x != T_NIL)                 //找到結點z要插入的位置    
    {
        if ( z->Max > x->Max)     //比較新插入的結點z與結點x的Max大小；
        {
            x->Max = z->Max;
        }
        y=x;
        if (z->INT.low < x->INT.low)
            x = x->left;
        else
            x = x->right;
    }
    z->p = y;
    if ( y == T_NIL)    //插入第一個結點作為根節點的情況  
        Root = z;
    else if (z->INT.low < y->INT.low)
        y->left = z;
    else    
        y->right = z;

    Root = Interval_Insert_Fixup(Root,z);    //插入完畢後，對紅黑樹的顏色進行修正
    return Root; 
}
Node * Establish(int A[][2],int len)   //建立紅黑樹
{
   Node * T,*node;
   int i=0;
   node=NULL;
   T_NIL=(Node *)malloc(sizeof(Node));  //建立T_NIL結點
   T_NIL->p=NULL;
   T_NIL->left=NULL;
   T_NIL->right=NULL;
   T_NIL->INT.low=-1;
   T_NIL->color=black;
   T_NIL->Max=0;
   T=T_NIL;
   for (i=0;i<len;i++)
   {
       node =(Node *)malloc(sizeof(Node));
       node->p =T_NIL;
       node->left=T_NIL;
       node->right=T_NIL;
       node->INT.low=A[i][0];         //以INT.low左作為關鍵字
       node->INT.high=A[i][1];         
       node->Max = A[i][1];           
       node->color=red;
       T=Interval_Insert(T,node);
   }
   return T;
}

void RB_Transplant(Node **T,Node * u,Node * v)  //結點替代函式
{
  if (u->p == T_NIL)
      *T = v;
  else if (u == u->p->left)
     u->p->left = v;
  else
     u->p->right = v;
  v->p = u->p;               //此處賦值無條件，v如果是T_NIL也要進行賦值
}
Node* Interval_Delete_Fixup(Node * T,Node * x)
{
    Node *w=NULL;
  while( x != T && x->color == black)      //迴圈迭代處理
  {
      if ( x == x->p->left )
      {
        w = x->p->right;
        if (w->color == red)             // case 1 ------> case 2 , case 3 ,case 4 
        {
            w->color = black;
            x->p->color =red;
            Left_Rotate(&T,x->p);
            w = x->p->right;
        }
        if ( w->left->color == black && w->right->color == black ) //case 2 ------>go on / stop
        {
            w->color = red;
            x = x->p;
        }
        else if ( w->right->color == black)   // case 3 ---->case 4---->stop
        {
           w->left->color = black;
           w->color =red ;
           Right_Rotate(&T,w);

           w = x->p->right ;                   //轉成case 4處理 
           w->color = x->p->color;
           x->p->color = black;
           w->right->color = black;
           Left_Rotate(&T,x->p);
           x = T;
        }
        else                               // case 4 ------------------->stop
        {
            w->color = x->p->color;
            x->p->color = black;
            w->right->color = black;
            Left_Rotate(&T,x->p);
            x = T;
        }
      }
      else
      {

          w = x->p->left;

          if (w->color == red)                // case 1 ------> case 2 , case 3 ,case 4 
          {
              w->color = black;
              x->p->color =red;
              Right_Rotate(&T,x->p);
              w = x->p->left;
          }
          if ( w->right->color == black &&a

相關推薦

演算法導論--動態順序統計與區間樹

通過在基礎的資料結構中新增一些附加資訊，來擴張一種標準的資料結構，然後編寫新的操作來支援所需要的應用。下面是介紹在紅黑樹的基礎上擴張的資料結構。 1.動態順序統計 動態順序統計可以在O(lgn)時間內確定任何的順序統計量(即在n個元素的集合中，能在O

演算法導論-動態規劃

動態規劃演算法 動態規劃（dynamic programming）是通過組合子問題來求解原問題的方法，它應用於解決子問題重疊的情況，即不同子問題具有公共的子問題。 通常動態規劃可以按照如下四個步驟進行設計： 1.刻畫一個最優解的結構特徵； 2.遞迴地定義最優解的值； 3.計算最優解的值，

演算法導論 第13章 紅黑樹（圖文詳細解說）

1、二叉查詢樹的不足 二叉查詢樹的基本操作包括搜尋、插入、刪除、取最大和最小值等都能夠在O(h)（h為樹的高度）時間複雜度內實現，因此能在期望時間O(lgn)下實現，但是二叉查詢樹的平衡性在這些操作中並沒有得到維護，其高度可能會變得很高，當其高度較高時，二叉查詢樹的效能就未

演算法導論學習-數學歸納法與迴圈不變式理解

數學歸納法： 最簡單和常見的數學歸納法是證明當n等於任意一個自然數時某命題成立。證明分下面兩步： 證明當n= 1時命題成立。 假設n=m時命題成立，那麼可以推導出在n=m+1時命題也成立。（m代表任意自然數） 這種方法的原理在於：首先證明在某個起點值時命題成立，然後證

演算法導論第十三章 紅黑樹

這碗雞湯我幹了，大家隨意。“雞湯”轉自：http://www.cnblogs.com/bakari/p/4900895.html       寫在前面：這一章真的把我害慘了，之前至少嘗試看過3遍，每次看之前都下定決定一定要把它拿下，可是由於內容較多，深度夠深，以致於

演算法導論——動態規劃之最長公共子序列（LCS）和最長迴文子序列（LPS）

有兩個字串A和B，假設為A=”abcbdab”,B=”bdcaba”;最長公共子序列（LCS）問題指的時找到A和B的一個公共的子串C，C的長度要是最長。 在這裡我們很明顯的發現最長子序列為”bcba” 用動態規劃的思想來考慮這個問題： 若A={a1,a2,

演算法導論20（van Emde Boas 樹）

#include<iostream> using namespace std; struct node { int u,min,max; node *summary; node **cluster; }; void vEB

演算法導論 第十四章：區間樹

區間樹是一種對動態集合進行維護的紅黑樹，具體設計如下： step1:基礎資料結構    我們選擇的基礎資料結構式紅黑樹，其中每個節點x包含一個區間域x.int,x的關鍵字為區間的低端點 x.int.low. step2:附加資訊     每個節點x除了區間資訊外，還包含一個

中位數和順序統計量---演算法導論學習筆記

演算法導論斷斷續續看了一小部分，但是還沒有寫過總結和筆記，很多思考和學習到的東西都隨著時間流失掉了（痛心）。 下面進入正題： 1.最大值和最小值問題 最簡單的確定一個有n個元素的集合中最小元素（最大元素）的方

演算法導論14.3區間樹 練習總結

14.3-1 寫出作用於區間樹的結點且在 O(1) 時間內更新 max 屬性的過程 LEFT-ROTATE 的虛擬碼。 ANSWER： 虛擬碼： LEFT-ROTATE(T, x) y = x.right y.max = x.max x.max =

演算法導論 學習筆記 第九章 中值和順序統計

本章其實只講了一個問題，那就是如何從一個數組當中用線性時間內找出第i個小的元素。 最小值和最大值 這個就比較簡單了，直接挨個比，執行時間就是線性的，而且這就是最好的辦法。 如何同時找出最小值和最大值咧？ 這個其實也簡單，那就記錄兩個資料唄。執行時間是找

樹狀數組的區間修改與單點查詢與區間查詢

pri 區間 stream 個數 普通 sca ace 一個數 n) 　　　　如何將普通樹狀數組升級 　　普通的單點修改單點查詢就不講了，從區間修改和單點查詢講起。 　　原來的值存在a[]裏面，多建立個數組c1[],註意：c1[i]=a[i]-a[i-1]。 　　那麽求a[

二叉搜尋樹增刪節點《演算法導論》12.3節

向二叉搜尋樹增加一個節點是比較簡單的，每個新節點都會成為樹上的新葉子，我們要做的是從根開始，沿著一條路徑，抵達安放新葉子的正確位置。這條路徑是怎樣找到的呢？ 路徑的起點自然是根節點了，把起點作為當前節點，和新節點比較大小，如果新節點較小，那麼新節點應該屬於當前節點的左子樹，於是選擇當前節點的左孩子作為新

動態規劃之鋼條切割問題，《演算法導論》15.1

動態規劃（dynamic programming），是一種解決問題的方法，它的思路是將大問題分解為子問題，然後合併子問題的解。與分治法將問題分解為彼此獨立的子問題不同，動態規劃應用於子問題相互重疊的情況。為了避免這些重疊部分（即子子問題）被重複計算，動態規劃演算法對每個子子問題只計算一次，並記錄在一個表

HDU 1166 敵兵佈陣【線段樹（單點更新與區間求和）】

C國的死對頭A國這段時間正在進行軍事演習，所以C國間諜頭子Derek和他手下Tidy又開始忙乎了。A國在海岸線沿直線佈置了N個工兵營地,Derek和Tidy的任務就是要監視這些工兵營地的活動情況。由於採取了某種先進的監測手段，所以每個工兵營地的人數C國都掌握的一清二楚,每個工兵營地的人數都有可能發生

演算法導論 第十三章：紅黑樹 筆記（紅黑樹的性質、旋轉、插入、刪除）

紅黑樹(red-black tree) 是許多“平衡的”查詢樹中的一種，它能保證在最壞情況下，基本的動態集合操作的時間為O(lgn) 。 紅黑樹的性質： 紅黑樹是一種二叉查詢樹，但在每個結點上增加一個儲存位表示結點的顏色，可以是RED或BLACK 。通過對任何一條從根到葉子的路徑上各個結

演算法導論 第十二章：二叉查詢樹 筆記（二叉查詢樹、查詢二叉查詢樹、插入和刪除、隨機構造的二叉查詢樹）

二叉查詢樹是一種樹資料結構，它與普通的二叉樹最大的不同就是二叉查詢樹滿足一個性質：對於樹中的任意一個節點，均有其左子樹中的所有節點的關鍵字值都不大於該節點的關鍵字值，其右子樹中的任意一個節點的關鍵字值都不小於該節點的關鍵字值。 在二叉查詢樹上可以進行搜尋、取最小值、取最大值、取指定節點的前驅

演算法導論 第四章：遞迴式 筆記（代換法、遞迴樹方法、主方法、主定理的證明）

三種解遞迴式的方法：代換法、遞迴樹方法、主方法。 代換法： 用代換法解遞迴式需要兩個步驟： 猜測解的形式； 用數學歸納法找出使解真正有效的常數。 如： T(n) = 2T(n/2) + n，這個是合併排序的執行時間的遞迴表示式。歸併排序法的執行時間是O(nlgn)，那麼我

演算法導論 第三章：函式的增長 筆記（Θ記號、O記號、Ω記號、o記號、ω記號、漸近記號的性質、標準記號與常用函式）

Θ記號： 該記號圓圈中是個M。Θ記號漸近地給出一個函式的上界和下界。 對於一個給定的函式g(n)，我們用Θ(g(n))來表示以下函式的集合： Θ(g(n))={f(n)：存在正常量c1、c2和n0，使得對於所有n⩾n0，有0⩽c1g(n)⩽f(n)⩽c2g(n)}。 即若存在正常

【線段樹與區間或】 woj 2820

描述 構造一個長度為n的非負整數序列x，滿足m個條件，第i個條件為x[li]|x[li+1]|…|x[ri]=pi。 輸入 第一行兩個整數n,m。接下來m行每行三個整數li,ri,pi。 輸出 如果存在這樣的序列x，第一行輸出Yes，第二行輸出n個不超過2^30-1的非負整數表示