視口變換在投影變換之後，視口變換的作用是將投影平面上的點轉換為螢幕上的點，這是一個縮放的過程。

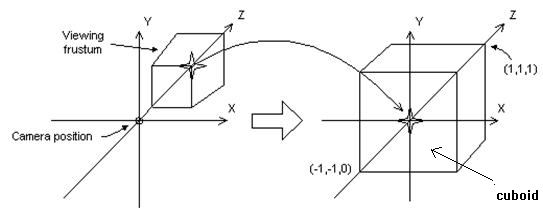
投影變換的作用是將viewing frustum（視景體）中的場景投影到一個平面上，這個平面就是投影平面，在DirectX中，使用近剪裁平面作為投影平面（z=1),關於透視投影的矩陣求解，請參考透視投影詳解

視口變換則是將這個cuboid中的物體變換到視口中，見下圖。

其中cuboid的座標範圍是

而viewport的座標範圍是

注：由上圖知，視口的起點為（X, Y），寬高分別為Width和Height，x軸向右為正，y軸向下為正，y軸的方向與三維座標正好相反。視口是一個2D平面，但是在viewport變換中，Z座標也是跟著變換的，只是在這個圖中沒有體現。

先求變換矩陣的第一列

Cuboid中的左上角點(-1, 1, 0, 1)對映到viewport中的起點(X, Y, MinZ, 1),

Cuboid中的右上角點(1, 1, 0, 1)對映到viewport中的點(X+Width, Y, MinZ, 1),

假設變換矩陣的第一列為[x’, y’, z’, 1]^T據矩陣乘法有

[-1, 1, 0, 1]* [x’, y’, z’, 1]^T = X

[1, 1, 0, 1]* [x’, y’, z’, 1]^T = X+Width

對應的兩個方程為

-1*x’ + 1*y’ + 0*z’ + 1*w’ = X

1*x’ + 1*y’ + 0*z’ + 1*w’ = X+Width

解之得

x’ = Width/2

y’ = 0

z’ = 0

w’ = x + Width/2

再求第二列

列方程（這裡省略了x’,z’，但結果不變，下同）

y’ + 1*w’=Y

-1*y’ + 1*w’=Y+Height

解之得

y’ = -Height/2

w’ = Y + Height/2

最後求第三列

列方程

0*z’ + 1*w’ = MinZ

1*z’ + 1*w’ = MaxZ

解之得

z’ = MaxZ – MinZ

w’ = MinZ

組合以上各列，得到視口變換矩陣