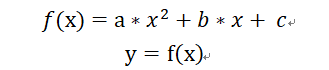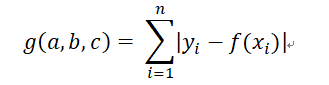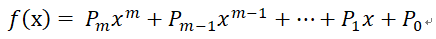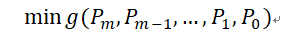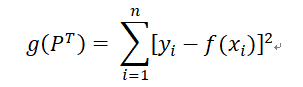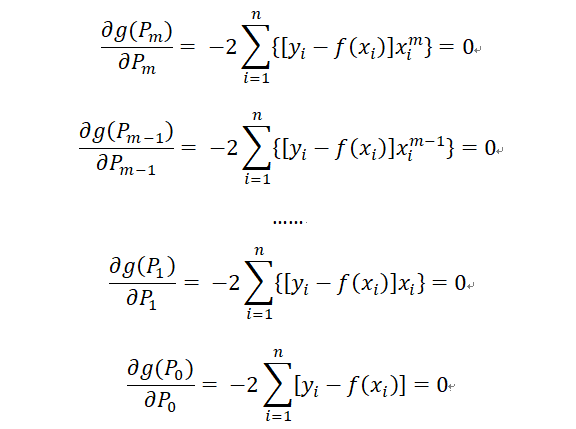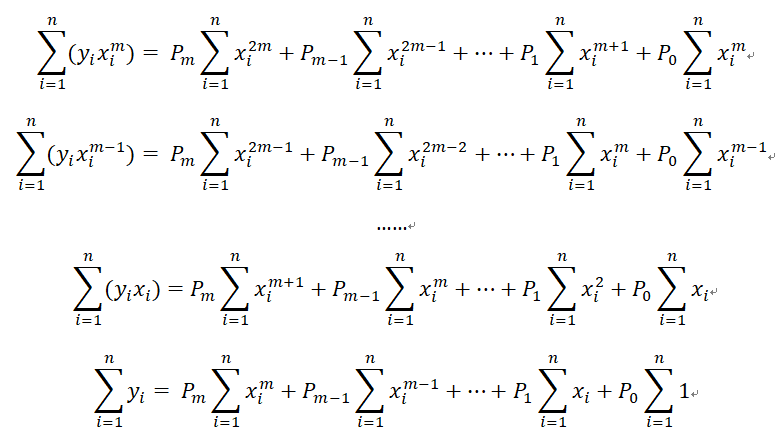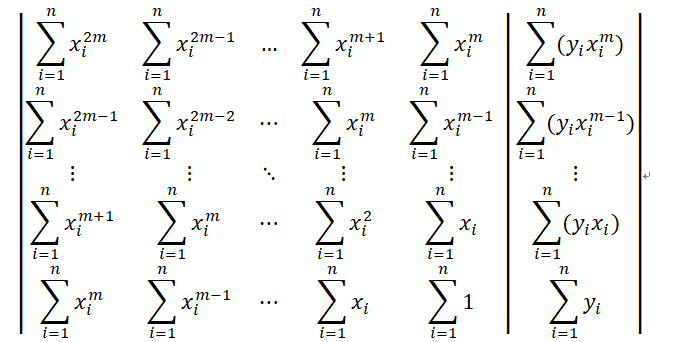線性最小二乘擬合算法實現-附C++原始碼
最近由於工作需要要做一套線性方程的擬合算法,在網上找了很多,不是用gsl就是用matlab做的,都不符合要求。實在找不到合適的於是就決定自己從頭寫,於是自己寫了一個,用了一段時間決得還行,就決定貼出來和大家分享一下,一方面可以順便騙點積分,另一方面也算是做個備忘吧。
原始碼可以在百度雲盤中下載:https://pan.baidu.com/s/1nvgjf41 密碼:8kqs
1、常用的一些函式的擬合算法,包括多項式、指數、對數和冪函式等 2、可以設定截距、權重 3、不依賴第三方庫,跨平臺執行
一、例項模型
有一種感測器(假設就是溫度感測器),感測器工作的時候會輸出一個電壓訊號u(mV),我們需要根據這個電壓訊號預測出感測器感知到的溫度t(℃)。假設通過大量的實驗資料我們知道溫度和電壓訊號呈如下的函式關係:

每個感測器由於自身的特性導致各自的a、b、c值都不一樣,因此在感測器出廠時我們需要對這個感測器進行標定,標定過程中,我們先在感測器的量程上均勻地挑選幾個點,然後分別用被測感測器和標準儀器測量各個點的值,預測方程式中的a、b、c值。假設最終測得的這些離散的點為 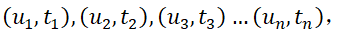
我們令
我們的目標就是求出a,b,c的值使得g(a,b,c)取得最小值。但是上面的式子中含有絕對值,使得式子變成一個非線性的函式而無法求解,可以令
推廣到更一般的形式,假設
最終目標就是計算
二、計算原理
通過上面的轉換,一個實際的問題就變成了一個求極值的問題。如下所示,這一類的函式是可以通過求每個分量的偏導數來計算極小值的,並且極小值就是最小值。證明過程就不寫出來了,如果感興趣可以自己去查(其實我也不知道怎麼證明,哈哈)
對各個分量求偏導數
展開上面的等式,得到了一個m+1維的一次方程組,然後就需要求解這個一次方程組了
寫成增廣矩陣的形式,如下所示
觀察這個矩陣發現左邊的矩陣為一個對角矩陣,得到這個矩陣後就可以根據高斯消元的方法求解,這裡就不詳細介紹了,最終化簡的結果就是
三、程式碼實現
有了上面的推算就可以編寫計算多項式線性迴歸的演算法程式碼了,C++編寫的演算法很方便,搗鼓了一陣子,就用C++寫了一套演算法,這些程式碼我分為三個部分,
1、高斯消元的部分,對應的檔案是augmentedmatrix.h和augmentedmatrix.cpp;
2、計算多項式的部分,對應的檔案是polynomialfit.h和polynomialfit.cpp;
3、基於多項式擬合的演算法計算指數、對數和冪函式的擬合值,對應的檔案是linearfit.h和linearfit.cpp。
除此之外還添加了
1、 權重的演算法
2、 部分函式還可以設定截距
3、 擬合優度的計算方式
但是測試過程中,發現除了不設定截距的多項式擬合的優度和Excel計算的優度能夠對應上之外,其他函式擬合的優度都無法和Excel對應上,也不知道Excel是如何計算擬合優度的。另外Excel也不能做權重的擬合,所以加了權重的擬合方式也沒有測試,但是加權值的效果確實做到了,優度也可以體現擬合結果的好壞。
四、測試效果
intmain(int,char**)
{
PolyfitTest();
// PowerTest();
// ExponentTest();
// LogarithmTest();
return0;
}
// 多項式擬合測試
voidPolyfitTest()
{
intdegree=2;
intcount=5;
doublesx[]={3.35,100.35,258.23,526.24,935.6};
doublesy[]={0.5225,10200.8225,67000.1929,277000.0176,697000.56};
doublew[]={1,0.02,0.01,0.005,0.001};
Polynomialpf;
pf.setAttribute(degree,false,1.0);
if(pf.setSample(sx,sy,count,false,w)&&
pf.process()){
pf.print();
std::cout<<"\ngoodness: "<<pf.getGoodNess()<<std::endl;
}else
std::cout<<"failed";
}
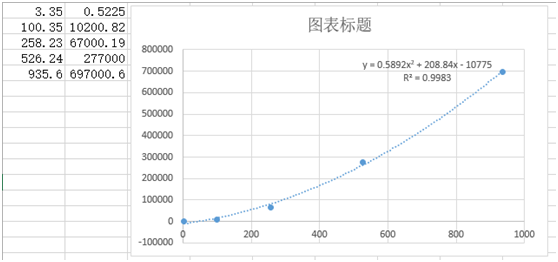
執行結果:
Polynomial Fit :
8.47470e+0119.82936e+008 1.22904e+006 6.91397e+011
9.82936e+0081.22904e+006 1823.77 8.16207e+008
1.22904e+0061823.77 5 1.0512e+006
results:0.58924 208.84 -10774.8
goodness: 0.998259
下面貼出Excel的計算結果
其他階次的多項式也試過了,Excel最多好像只能擬合到6階,這套程式碼設定最高到32階,感覺也夠了。
就寫到這裡,也不知道有沒有講清楚,由於時間倉促、水平有限,程式碼裡面當然也難免會有不足之處,歡迎大家批評指正。