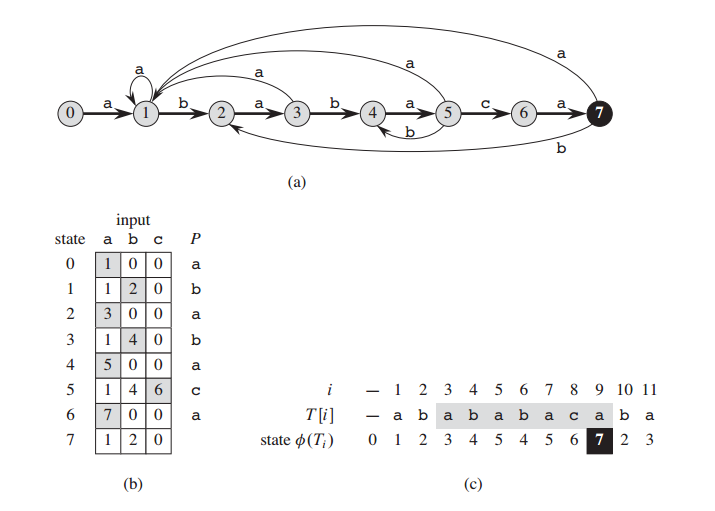
定義這裡狀態 的概念：狀態代表當前已經匹配的字元個數。狀態轉移代表，在當前狀態下，輸入一個字元讓當前狀態發生變化。

關於自動機原理，請參考其他編譯原理書籍

自動機M是一個元組（Q，q， A， ∑，δ）

Q是狀態的有限集合

q∈Q是一個初始狀態

A屬於Q是 特殊的接受狀態集合

∑是有限輸入字母表

有限自動機開始於狀態q，每次讀入輸入字串的一個字元。如果有限自動機在狀態q的時候讀入了字元a，則它從狀態q轉變為δ(q,a)。每當其當前狀態q輸入A時，就說自動機Ｍ接受了迄今為止所讀入的字串。沒有接受的輸入稱為被拒絕的輸入。
有限自動機Ｍ引入一個函式ф,稱為終態函式，它是從∑*到Q的函式，滿足ф(w)是M在掃描字串w後終止時的狀態。因此，當且僅當ф(w)∈A時，M接受字串w。我們可以用轉移函式遞迴定義ф：

有限自動機Ｍ引入一個函式ф,稱為終態函式，它是從∑*到Q的函式，滿足ф(w)是M在掃描字串w後終止時的狀態。因此，當且僅當ф(w)∈A時，M接受字串w。我們可以用轉移函式遞迴定義ф：

ф（ε）=q；

ф（wa）=δ(ф（w）,a)

    考慮以下兩種情況。第一種情況是，a=P[q+1],使得字元a繼續匹配模式。在這種情況下，由於δ(q,a)=q+1，轉移沿著自動機的主線繼續進行。第二張情況a≠P[q=1]，使得字元a不能繼續匹配模式。這時我們必須 找到一個更小的 子串，它是P的字首同時也是Ti的 字尾。因為當建立字串匹配自動機時，預處理匹配模式和自己， 轉移函式很快得出最長的這樣的較小P字首

#include<iostream>
#include<vector>
#include<map>
#include<string.h> 
using namespace std;

bool Matching_Prefix(const char *P,int k,int q,char a){
	if(k==0)
	return true;
	if(k==1){
		return P[0]==a;
	}
	return P[k-1]==a&& (strncmp(P,P+q-k+1,k-1)==0);
}

vector<map<char,int>> Compute_Transition_Function(const char *P,const char*input_character ){
	int m=strlen(P);
	int j=0,k;
	cout<<m<<endl;
	vector<map<char,int> >transition_map(m+1);
	for(int i=0;i<m;i++){ 
		j=0;
		cout<<"p:"<<i<<endl;                        //狀態i 
		while(input_character[j]!='\0'){
		 k= min(m+1,i+2);
		do{
			k=k-1;
		}while(!Matching_Prefix(P,k,i,input_character[j]));
		transition_map[i][input_character[j]]=k;
		cout<<"狀態p:"<<i<<",    輸入字元"<<input_character[j]<<",    k:"<<k<<endl;   //輸出狀態轉移函式 
		j++; 
		}	
	}
	return 	transition_map;
}


void Finite_Automaton_Matcher(char *T,char*P,vector<map<char,int>>transition_map){	
	int n=strlen(T);
	int m=strlen(P);
	int q=0 ;   //初始狀態為0	
	 for(int i=0;i<n;i++){
	 q = transition_map[q][T[i]];
	 if(q==m)
	 cout<<"Pattern occurs whit shift"<<i-m<<endl;	
	 }
	 
}


int main(){
	const char *input_character="abcdefghijklmnopqrstuvwxyz";  //有限輸入字母表 
	char T[]="abdfdfsdklfdjgkjgdkjerdfgfdg";
	char P[11]= "dklfdjgkj";
	vector<map<char,int>>transition_map=Compute_Transition_Function(P,input_character);
	Finite_Automaton_Matcher(T,P,transition_map);
	return 0;
	
} 
 

    預處理Computer_Transition_Function的執行時間為Θ（m^3 |∑|）。當然預處理可以改進為Θ（m|∑|），所以最後的時間為Θ(n)匹配時間加上Θ(m)的預處理時間。