公眾號 資料精簡DataSimp

　　資料精簡DataSimp分享：資訊與資料探勘分析、資料科學研究前沿、資料資源現狀和資料簡化基礎的學科知識、技術應用、產業科研、人物機構、新聞活動等資訊。歡迎大家積極參與投稿，為資料科學產學研做貢獻，使國人儘快提高人類資訊管理能力，提高社會資訊流通效率。本期內容：AlphaGo演算法論文《精通圍棋博弈的深層神經網路和樹搜尋演算法》漢譯（DeepMind圍棋人工智慧團隊2016.1.28發表在《自然》雜誌的nature16961原文翻譯，人工智慧之機器學習經典收藏版）、公號附錄（大資料儲存單位和資料簡化DataSimp公眾號簡介）。

　　精通圍棋博弈的深層神經網路和樹搜尋演算法

　　作者：

　　①戴維·斯爾弗1*，②黃士傑1*，③克里斯·J。·麥迪遜1，④亞瑟·格斯1，⑤勞倫特·西弗瑞1，⑥喬治·範登·德里施1，⑦朱利安·施立特威澤1，⑧揚尼斯·安東諾婁1，⑨吠陀·潘聶施爾萬1，⑩馬克·蘭多特1，⑪傘德·迪勒曼1，⑫多米尼克·格魯1，⑬約翰·納姆2，⑭納爾 卡爾克布倫納1，⑮伊利亞·薩茨基弗2，⑯蒂莫西·李烈克萊普1，⑰馬德琳·裡奇1，⑱科瑞·卡瓦口格魯1，⑲託雷·格雷佩爾1，和⑳戴密斯·哈薩比斯1

　　作者單位說明：1谷歌DeepMind，英國倫敦EC4A 3TW，新街廣場5號。2谷歌，美國加利福尼亞州94043，景山，劇場路1600號。*這些作者對這項工作作出了同等貢獻。

　　中文翻譯者說明*：

　　原文發表在《自然》2016年1月28日第529卷，484-489頁，保留所有權利。©英國麥克米倫出版公司2016版權。本文漢語譯者基於“忠於原文”原則全文翻譯。同時參考自然雜誌官網http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html，由十五部分組成：摘要、導言、策略網路的監督學習、策略網路的強化學習、估值網路的強化學習、基於策略網路和估值網路的搜尋演算法、AlphaGo博弈算力評估、討論、方法、參考文獻、致謝、作者資訊、擴充套件資料影象和表格、補充資料和網站評論。本文翻譯到算力評估。網站提示：郵件可發至戴維·斯爾弗（

　　歡迎讀者閱讀原文，加強學習理解、掌握應用核心資訊科技。時間倉促，疏漏之處難免，敬請提出寶貴意見。中文譯者：秦隴紀-資料簡化DataSimp（貢獻3/5以上），姬向軍-陝西師範大學，楊武霖-中國空間技術研究院，池紹傑-北京工業大學。（轉載本公號文章請註明作者、出處、時間等資訊，如“此文轉自：資料簡化DataSimp英譯組秦隴紀等人；©微信公號：資料簡化DataSimp；2016.3.15Tue譯著©。”字樣，詳情郵件諮詢[email protected]，本文正在投稿，轉載請保留本資訊。歡迎資料科學和人工智慧學界、產業界同仁賜稿。）

　　摘要：

　　由於海量搜尋空間、評估棋局和落子行為的難度，圍棋長期以來被視為人工智慧領域最具挑戰的經典遊戲。這裡，我們介紹一種新的電腦圍棋演算法：使用“價值網路”評估棋局、“策略網路”選擇落子。這些深層神經網路，是由人類專家博弈訓練的監督學習和電腦自我博弈訓練的強化學習，共同構成的一種新型組合。沒有任何預先搜尋的情境下，這些神經網路能與頂尖水平的、模擬了千萬次隨機自我博弈的蒙特卡洛樹搜尋程式下圍棋。我們還介紹一種新的搜尋演算法：結合了估值和策略網路的蒙特卡洛模擬演算法。用這種搜尋演算法，我們的程式AlphaGo與其它圍棋程式對弈達到99.8%的勝率，並以5比0擊敗了人類的歐洲圍棋冠軍。這是計算機程式第一次在標準圍棋比賽中擊敗一個人類職業棋手——以前這被認為是需要至少十年以上才能實現的偉業。

　　導言：

　　完美資訊類遊戲都有一種最優值函式v*（s），從所有遊戲者完美對弈時每一棋盤局面或狀態s，判斷出遊戲結果。這類遊戲可以通過遞迴計算一個約含bd種可能落子情況序列的搜尋樹，求得上述最優值函式來解決。這裡，b是遊戲廣度（每個局面可合法落子的數量），d是遊戲深度（對弈步數）。在國際象棋（b≈35，d≈80）1，特別是圍棋（b≈250，d≈150）1等大型遊戲中，雖然窮舉搜尋並不可取2，3，但有兩種常規方法可以減少其有效搜尋空間。第一種方法，搜尋深度可以通過局面評估來降低：用狀態s截斷搜尋樹，將s的下級子樹用預測狀態s結果的近似值函式v（s）≈v*（s）代替。這種做法在國際象棋4，跳棋5和奧賽羅6中取得了超過人類的效能；但由於圍棋7的複雜性，這種做法據信在圍棋中變得棘手。第二種方法，搜尋廣度可以用局面s中表示可能落子a的策略函式p（a|s）產生的概率分佈的弈法抽樣來降低。例如，蒙特卡洛走子演算法8搜尋到最大深度時無任何分支，而是用策略變數p為對弈雙方的長弈法序列取樣。大體上，這些走子行為提供了一種有效的局面評估，在五子棋8、拼字遊戲9和低水平業餘圍棋比賽10中均實現了超越人類水平的效能。

　　蒙特卡洛樹搜尋（MCTS）11，12用蒙特卡洛走子來估算一個搜尋樹中每個狀態的值。隨著更多模擬情況的執行，該搜尋樹生長變大、相關值變得更加準確。隨著時間的推移，通過選擇那些較高估值的子樹，搜尋過程中選擇弈法的策略也得到了提高。該策略漸進收斂於最優弈法，對應的估值結果收斂於該最優值函式12。當下最強的圍棋程式都基於MCTS，通過預測人類高手落子情況而訓練的一些策略，來增強效能13。這些策略大都把此搜尋過程限制在高概率弈法，以及走子時的弈法取樣。該方法已經在很強的業餘博弈中取得了成功13–15。然而，以前的做法僅限於淺層策略13–15，或某些基於一種帶輸入型特徵值的線性函式組合的估值函式。

　　近來，深度卷積神經網路在視覺領域達到前所未有的高效能：例如影象分類17、人臉識別18、雅達利遊戲19。他們用重疊排列的多層神經元，逐步構建影象的區域性抽象表徵20。我們在圍棋中採用類似架構：通過把棋局看做為一個19×19的影象，使用若干卷積層構造該局面的表徵值。用這些神經網路，我們來減少有效深度及搜尋樹廣度：用一個估值網路評估棋局，用一個策略網路做弈法取樣。

　　我們用一種由機器學習若干階段組成的管道來訓練這些神經網路（圖1）。開始階段，我們直接使用人類高手的落子弈法訓練一種有監督學習（SL）型走棋策略網路pσ。此階段提供快速、高效的帶有即時反饋和高品質梯度的機器學習更新資料。類似以前的做法13，15，我們也訓練了一個快速走棋策略pπ，能對走子時的弈法快速取樣。接下來的階段，我們訓練一種強化學習（RL）型的走棋策略網路pρ，通過優化那些自我博弈的最終結果，來提高前面的SL策略網路。此階段是將該策略調校到贏取比賽的正確目標上，而非最大程度的預測準確性。最後階段，我們訓練一種估值網路Vθ，來預測那些採用RL走棋策略網路自我博弈的贏家。我們的程式AlphaGo，用MCTS有效結合了策略和估值網路。

　　圖1：神經網路訓練管道和架構

　　左邊圖1a，一種快速走子策略pπ和監督學習（SL）策略網路pσ被訓練，用來預測一個局面資料集中人類高手的落子情況。一種強化學習（RL）策略網路pρ按該SL策略網路進行初始化，然後對前一版策略網路用策略梯度學習來最大化該結果（即贏得更多的比賽）。通過和這個RL策略網路自我博弈，產生一個新資料集。最後，一種估值網路vθ由迴歸訓練的，用來預測此自我博弈資料集裡面局面的預期結果（即是否當前玩家獲勝）。右邊圖1b，AlphaGo神經網路架構的示意圖。圖中的策略網路表示：作為輸入變數的棋局s，通過帶引數σ（SL策略網路）或ρ（RL策略網路）的許多卷積層，輸出合法落子情況a的概率分佈或，由此局面概率圖來呈現。此估值網路同樣使用許多帶引數θ的卷積層，但輸出一個用來預測局面sʹ預期結果的標量值vθ（sʹ）。

　　1、策略網路的監督學習

　　訓練管道第一階段，我們按以前的做法用監督學習預測圍棋中高手的落子情況13，21–24。此SL策略網路pσ（a|s）在帶有權重陣列變數σ和整流器非線性特徵值陣列的卷積層間交替使用。最終的softmax層輸出一個所有合法落子情況的概率分佈a。此策略網路的輸入變數s是一個棋局狀態的簡單標識變數（見擴充套件資料表2）。策略網路基於隨機取樣的棋盤情形-操作對（s，a）做訓練：採用隨機梯度升序法，在選定狀態s時，取人類落子a的最大相似度，

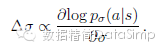
　　我們用KGS圍棋伺服器上的3000萬種棋局，訓練了一個13層策略網路，稱之為SL策略網路。對比其他研究團體提交的44.4%頂尖水準，該網路在一個公開測試資料集上預測高手落子情況：採用全部輸入型特徵值可達57.0%精度，只採用原始棋局和落子歷史資料做為輸入可達55.7%（全部結果在擴充套件資料表3）24。準確性上小的改進，可導致算力大幅提高（圖2a）；較大網路亦可實現更好的精度，但在搜尋過程中的評價會變慢。我們也訓練了一個快速、但低準確度的走子策略pπ（a|s），採用一種帶權重π的小圖式特徵量的線性softmax層（參見擴充套件資料表4），這樣，僅用2微秒選擇一種弈法可以達到24.2%的精確度，而不是此策略網路的3毫秒。

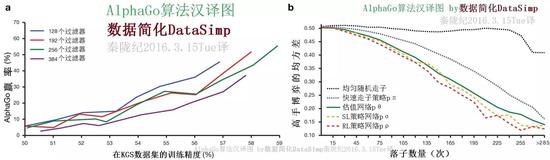
　　圖2：策略和估值網路的算力和準確性。

　　圖2a，標尺圖展示作為一個他們訓練精確性函式的策略網路博弈算力。每個卷積層分別有128，192，256和384個過濾器的策略網路在訓練期間被定期評估；此圖顯示AlphaGo運用那種策略網路與比賽版AlphaGo對戰的勝率。圖2b，該估值網路和不同策略走子弈法之間的估值精度比較。從人類專家博弈中做局面和結果取樣。每局都由一個單一向前傳遞的估值網路vθ，或100步走子情況的平均結果做評估，用均勻隨機走子，快速走子策略pπ，SL策略網路pσ或RL策略網路pρ等使局面充分被評估。此預測值和實際博弈間的均方差，繪製在博弈階段（多少落子已經在給定局面）。

　　2、策略網路的增強學習

　　訓練管道第二階段，旨在用策略梯度型增強學習（RL）來提高之前的策略網路25，26。這種RL策略網路pρ在結構上與SL策略網路相同，其權重ρ被初始化為相同值：ρ=σ。我們使其在當前策略網路pρ和某個隨機選擇的上次迭代產生的策略網路之間進行對弈。這種方法的訓練，要用隨機化的存有對手穩定態的資料池，來防止對當前策略的過度擬合。我們使用報酬函式r（s），對所有非終端時間步長t<T時，賦值為0。其結果值zt = ± r（sT）是博弈結束時的終端獎勵：按照當前博弈者在時間步長t時的預期，給勝方+1、敗方−1。權重在每一次步長變數t時，按照預期結果最大值的方向，進行隨機梯度升序更新25。

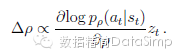
　　博弈中我們評估該RL策略網路的效能，從弈法輸出概率分佈對每一次落子取樣為。與SL策略網路正面博弈時，RL策略網路贏得了80%以上。我們還用最厲害的開源圍棋程式Pachi14來測試。那是一種複雜的蒙特卡洛搜尋程式——KGS伺服器上排名第二的業餘選手dan，每個落子要執行10萬次模擬。不用任何搜尋，RL策略網路贏得了85%與Pachi的對弈。對照以前的頂尖水平，僅基於卷積網路的監督學習與Pachi23對弈只能贏得11%、與較弱程式Fuego24對弈為12%。

　　3、估值網路的增強學習

　　最後階段的訓練管道聚焦在對棋局的評估，用一個估值函式vp（s）做估計，給棋局s中兩個使用策略p的博弈者預測結果28，29，30。

　　理想情況下，我們想知道完美博弈v*（s）中的該最優值函式；實踐中，我們用值函式代替做估算，作為最強策略用在RL策略網路pρ。我們用帶權重陣列θ的估值網路vθ（s）對此估值函式做近似，

　　。該神經網路具有一種與此估值函式相似的結構，但輸出一個單一預測，而不是一個概率分佈。我們用狀態-結果對（s， z）迴歸，訓練該估值網路權重，使用隨機梯度降序來最小化該預測值vθ（s）和相應結果z間的均方差（MSE），

　　用包含全部博弈的資料集，來預測對弈結果的幼稚做法，會導致過度擬合。其錯誤在於：連續棋局是緊密相關的，不同處只有一枚棋子，但其迴歸目標被該完整對弈所共用。我們用這種方法在KGS資料集做過訓練，該估值網路記住了那些博弈結果，並沒有推廣到新棋局，相比此訓練集上的0.19，此測試集上達到了0.37的最小均方差（MSE）。為了緩解這個問題，我們生成了一個新的含有3000萬明顯不同棋局的自我博弈資料集，其每個取樣都來自於某一單獨對弈。每一場對弈都是在上述RL策略網路與自身之間進行，直到博弈結束。在該資料集上的訓練，採用訓練和測試資料集分別可達到0.226和0.234的均方差，這表明最小的過擬合。圖2b顯示了上述估值網路的棋局評估精度，相比使用快速走子策略pπ的蒙特卡洛走子程式，此估值函式一貫都是更加準確。一種vθ（s）單一評價函式也接近使用RL策略網路Pρ的蒙特卡洛程式的精度，且使用少於15000次的計算量。

　　4。基於策略網路和估值網路的搜尋演算法

　　AlphaGo在一種採用前向搜尋選擇弈法的MCTS演算法裡，結合使用策略和估值網路（圖3）。每個搜尋樹邊界（s， a）儲存：弈法值Q（s， a），訪問計數N（s， a），和前驅概率P（s， a）。從當前根狀態出發，該搜尋樹用模擬（指已完成的博弈中做無備份降序）做遍歷。在每次模擬的每個時間步長t，從狀態st內選出一個弈法at，

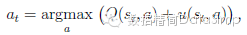
　　當滿足，最大弈法值加上與前驅概率成正比、但與訪問計數成反比的獎勵值：

　　，能有效促進對搜尋空間的探索。當這個遍歷在步驟L，搜尋一個葉節點sL時，該葉節點可能被展開。該葉節點的局面sL僅通過SL型策略網路pσ處理一次。該輸出概率被儲存為每次合法弈法a的前驅概率。

　　這個葉節點通過兩種不同方式被評估：一種是通過估值網路vθ（sL）；第二種是，通過一種隨機落子的結果值zL，直到使用快速走子策略pπ在步長T時結束博弈。這些評價被組合起來，用一種混合引數λ，進入一個葉節點估值V（sL）：

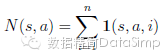
　　模擬結束時，遍歷過的所有邊界其弈法值和和訪問計數就會被更新。每個邊界累加其訪問計數值，和所有經過該邊界做的模擬的平均估值：

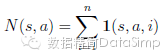
　　式中是其第i次模擬的葉節點，1（s， a， i）代表第i次模擬中一個邊界（s， a）是否被訪問。當該搜尋結束時，本演算法選擇這次初始局面模擬的訪問計數最多的弈法來落子。

　　圖3：AlphaGo的蒙特卡洛樹搜尋。

　　圖3a，每次模擬都遍歷帶最大弈法值Q的那個邊界節點，與一個由那個邊界節點儲存的前驅概率產生的獎勵值u（P）相加。圖3b，此葉節點可能被展開；新節點採用策略網路pσ，其輸出概率值P被儲存在每個弈法的前驅概率P中。圖3c，模擬結束後，此葉節點被兩種方法評估：採用估值網路vθ；和博弈最後用快速落子策略pπ進執行一次走子，然後用函式r計算此贏家的估值。圖3d，弈法值Q被更新，用來追蹤所有估值r（·）的中間值和那個弈法下面的子樹vθ（·）。

　　值得注意的是，此AlphaGo的SL策略網路pσ比那個加強型RL策略網路pρ表現地更好，主要原因在於人類選擇最有前景落子中一種可變化的弈法，而RL僅對該單次落子做最優化。然而，從強化後的RL策略網路中推導的估值函式，在AlphaGo的效能要優於SL策略網路推匯出的估值函式。

　　跟傳統啟發式搜尋相比，策略和估值網路需要高出幾個數量級的計算量。為了有效結合MCTS和深度神經網路，AlphaGo採用非同步多執行緒搜尋，在多CPU上執行模擬、多GPU平行計算策略和估值網路。本最終版AlphaGo使用了40個搜尋執行緒、48個CPU和8個GPU。我們也應用了一種分散式AlphaGo版本，部署在多臺機器上、40個搜尋執行緒、1202個CPU和176個GPU。方法章節提供非同步和分散式MCTS全部細節。

　　5.AlphaGo博弈算力評估

　　為了評估AlphaGo，我們在幾個版本的AlphaGo和其它幾種圍棋程式之間運行了一場內部競賽，包括最強商業軟體Crazy Stone13，和Zen，和最強開源程式Pachi14和Fuego15。所有這些程式基於高效能MCTS演算法。此外，我們納入了開源程式GnuGo，一種使用優於MCTS的頂級水平搜尋演算法的圍棋程式。在比賽中，所有軟體每一步都只有5s中的計算時間。

　　（未完待續。感謝翻譯過程中Dr何萬青Dr餘凱ETS顏為民等人的譯文建議。歡迎大家關注譯文質量，我們共同提高。）

　　附錄一、大資料儲存單位（TB以上）

　　計算機儲存最小的基本單位是bit，按順序給出所有計量單位：bit位（無法分割）、Byte位元組（10^0）、KB千位元組（10^1）、MB兆位元組（10^3）、GB吉位元組（10^6）、TB太位元組（10^9）、PB拍位元組（10^12）、EB艾位元組（10^15）、ZB澤位元組（10^18）、YB堯位元組（10^21）、BB（10^24）、NB（10^27）、DB（10^30）。大資料儲存單位大都TB以上，按照進率1024（2的十次方）來計算：

　　1 TB = 1，024 GB（Gigabyte吉位元組） = 1，048，576 MB（Megabytes兆位元組）；

　　1 PB（Petabyte千萬億位元組，拍位元組） = 1，024 TB（Terabytes） = 1，048，576 GB；

　　1 EB（Exabyte百億億位元組，艾位元組） = 1，024 PB（Petabytes） = 1，048，576 TB；

　　1 ZB（Zettabyte十萬億億位元組，澤位元組） = 1，024 EB（Exabytes） = 1，048，576 PB；

　　1 YB（Yottabyte一億億億位元組，堯位元組） = 1，024 ZB（Zettabytes） = 1，048，576 EB；

　　1 BB（Brontobyte一千億億億位元組） = 1，024 YB（Yottabytes） = 1，048，576 ZB；

　　1 NB（N？Geopbyte？沒查到翻譯） = 1，024 BB（Brontobytes） = 1，048，576 YB；

　　1 DB（？沒查到） = 1，024 NB = 1，048，576 BB。

　　注：進位制單位全稱及譯音 yotta [堯]它 Y。 10^21， zetta [澤]它 Z。 10^18， exa [艾]可薩 E。 10^15， peta [拍]它 P。 10^12， tera [太]拉 T。 10^9， giga [吉]咖 G。 10^6， mega [兆] M。 10^3“兆”為百萬級數量單位。（秦隴紀16科普版）