這幾天忙著找工作，看到有去阿里面試的同學遇到了堆排序的問題，因此就去網上看部落格學習，但看半天實在看不懂，只好把演算法導論拿出來啃，沒想到還挺簡單，所以在這裡分享給大家。

0.堆簡介

堆（二叉堆）可以視為一棵完全的二叉樹，完全二叉樹的一個“優秀”的性質是，除了最底層之外，每一層都是滿的，這使得堆可以利用陣列來表示（普通的一般的二叉樹通常用連結串列作為基本容器表示），每一個結點對應陣列中的一個元素。

如下圖，是一個堆和陣列的相互關係

對於給定的某個結點的下標 i，可以很容易的計算出這個結點的父結點、孩子結點的下標：

Parent(i) = i/2，i 的父節點下標

Left(i) = 2i，i 的左子節點下標

Right(i) = 2i + 1，i 的右子節點下標

二叉堆一般分為兩種：最大堆和最小堆。

本文介紹的是最大堆。

1.堆排序演算法介紹

一個堆在程式中可以簡單的用陣列描述，那麼堆排序演算法可以分為二步：將無序的陣列構造成一個最大堆，對該最大堆進行排序。

其中第一步又可以分成兩步：

》區域性構建成最大堆

1）維護堆的性質

演算法清晰明瞭，分別找到i元素的左孩子和右孩子，若左孩子與右孩子中有比i元素大的，找到最大的那個元素，並且與i元素交換位子，然後對交換位子的那個最大元素再次呼叫MaxHeap方法。注意，此演算法成立的條件是i元素的左子樹與右子樹都是最大堆!!!

》利用迴圈將整個陣列構建成最大堆

2）建堆

我們在陣列中從size/2到1呼叫第一步的MaxHeap方法，那麼顯然可以保證整個陣列都可以維持最大堆的性質。

注意：要從size/2到1而不是1到size/2。因為第一個步驟成立是有條件的，i元素的左子樹與右子樹都是最大堆，所以我們只能從堆的倒數第二層，也就是高度為2的節點開始，那麼才能保證第一個步驟是正確的。

》對建好的堆進行排序

3）對建好的堆進行排序

將當前堆中的最大值A[1]與堆中的末尾元素進行交換，接下來將堆的大小減一，對縮小的堆進行MaxHeapify(即第一步操作)，接下來的操作就是不斷重複這個過程，直到陣列有序

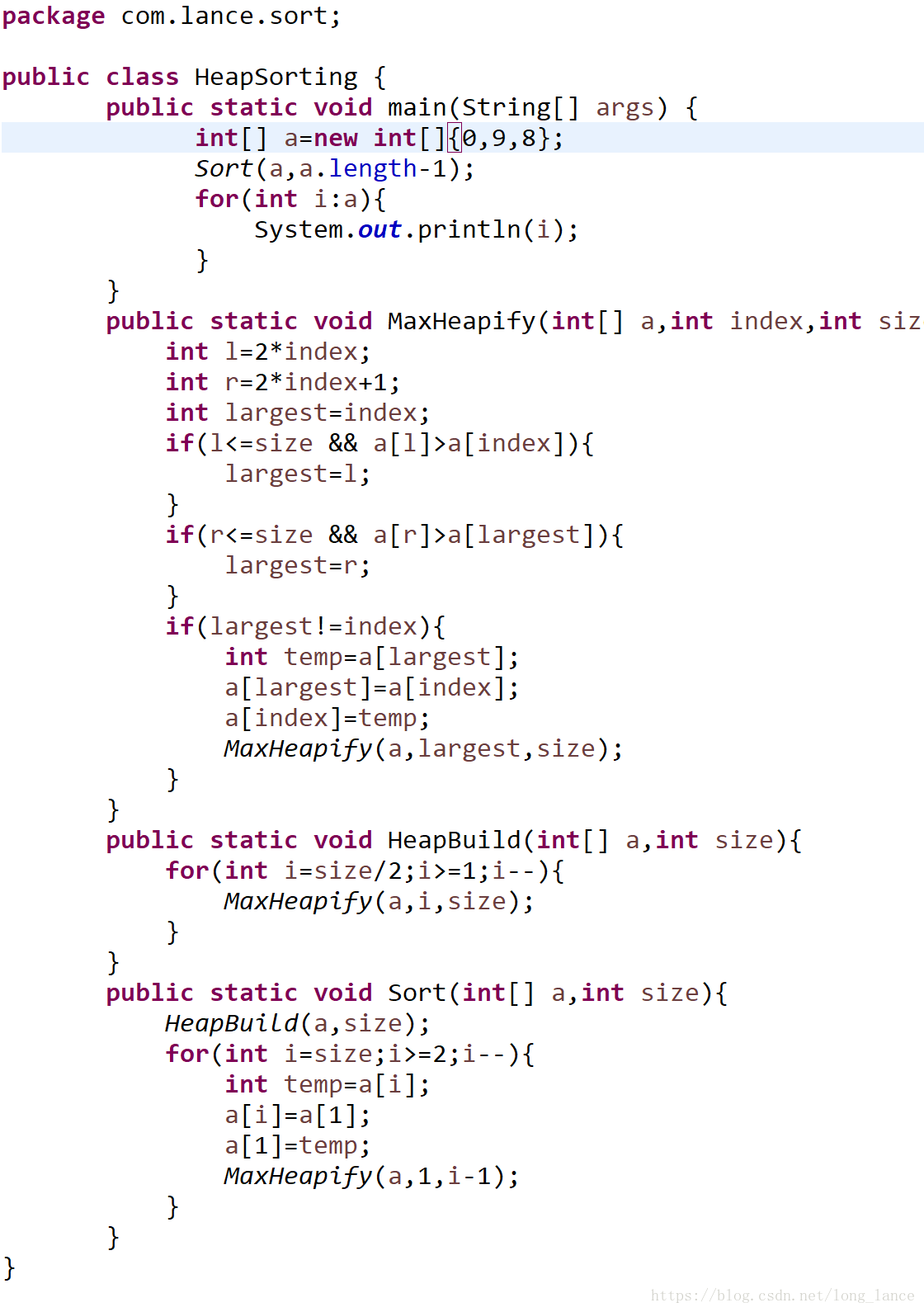
4.程式碼總結

注意：MaxHipify中l<=size與r<=size不要寫成l<size,r<size,否則程式碼就是錯的，筆者犯了這個錯誤，找了好久。

特意用了圖片，沒有用程式碼段，希望讀者閱讀完部落格能自己按照思路嘗試寫出程式碼，不要成為CV戰士。

注意:轉載本文請註明出處與作者，謝謝！！