Description

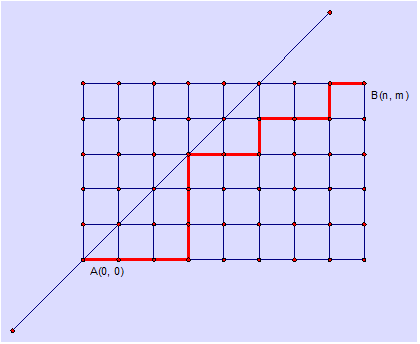
某城市的街道呈網格狀，左下角座標為A(0, 0)，右上角座標為B(n, m)，其中n >= m。現在從A(0, 0)點出發，只能沿著街道向正右方或者正上方行走，且不能經過圖示中直線左上方的點，即任何途徑的點(x, y)都要滿足x >= y，請問在這些前提下，到達B(n, m)有多少種走法。

nput

輸入檔案中僅有一行，包含兩個整數n和m，表示城市街區的規模。

Output

輸出檔案中僅有一個整數和一個換行/回車符，表示不同的方案總數。

Sample Input

輸入1：

6 6

輸入2：

5 3

Sample Output

輸出1：

132

輸出2：

28

Data Constraint

50%的資料中，n = m，在另外的50%資料中，有30%的資料：1 <= m < n <= 100

100%的資料中，1 <= m <= n <= 5 000

Analysis

這道題類似我以前做的題 ~~可惜的是我忘了~~QAQ

好吧，其實這道題就是說在不超過x<=y這條直線上的，只能向上向右走，從（1,1），走到（n,m)的方案是多少?

其實這道題可以看成一個楊輝三角（不要問我為什麼，暴力一下便知道，自己腦補。。。）所以我們可以考慮組合數。

那麼我們可以沿題目給的那條線，將終點對稱過去，找到一個對稱點
我們可以發現從起點到對稱點的路徑再對稱回來的路徑是一條不合法的路徑，
所以Ans=無限制亂走方案數-起點走到對稱點的方案數。
其實就是所有的方案數-不合法的方案數即為合法方案數。
所以這裡有公式給參考

這裡介紹一個快速的方法（個人認為是挺快的，起碼比普通高精度快，比壓位好打）
考慮到化簡後是個除法，所以可以求出分子的約數，與分母的約數，
千萬不要先乘，這樣會炸。我們可以把它變成因子連乘的形式，
如3！=1*2*3,這樣分子求出約數後，在求出分母約數，最後約分（具體怎麼做可以看下面我的程式，或自己腦補），因為答案保證它一定是整數，就可以保證正確率了。
最後只要做一遍剩下因子的高精乘就好了。

不用打除法是否棒棒的 o((>ω< ))o

CODE

#include <cstdio>
#include <cmath>
#include <iostream>
#include <cstring>
#include <algorithm>
#define fo(i,a,b) for (int i=a;i<=b;i++)
#define fd(i,a,b) for (int i=a;i>=b;i--)
#define N 100005
using namespace std;
int a[N],b[N],l=1;
int n,m;
void Fact(int k)
{
    int x=0;
    fo(i,1,l)
    {
        b[i]=b[i]*k+x;
        x=b[i]/10;
        b[i]%=10;
    }
    while (x>0)
    {
        b[++l]=x%10;
        x/=10;
    }
}
void ys(int x,int k)
{
    fo(i,2,x)
    while (x%i==0)
    {
        a[i]+=k;
        x/=i;
        if (x<=1) return;
    }
}

int main()
{
    /*((n+1-m)(n+m)!) / (m!(n+1)!)
    */
    scanf("%d%d",&n,&m);
    int k=1;
    ys((n+1-m),k);
    fo(i,1,m+n) ys(i,k);
    k=-1;
    fo(i,1,n+1) ys(i,k);
    fo(i,1,m) ys(i,k);
    b[1]=1;
    fo(i,2,n+m)
    if (a[i]!=0) 
    fo(k,1,a[i]) Fact(i);
    fd(i,l,1) printf("%d",b[i]);
    return 0;
}