JZOJ.3431【GDOI2014模擬】網格 解題報告
網格
題目描述
某城市的街道呈網格狀,左下角座標為
樣例輸入
樣例輸出
資料範圍
題解
關於這種不能穿過某條直線的網格行走問題,先講一下怎麼做。
我們知道,答案就等於走到點(
我們還知道由點(
所以我們現在只需求得穿過這條直線的路徑數量就可以知道答案了。
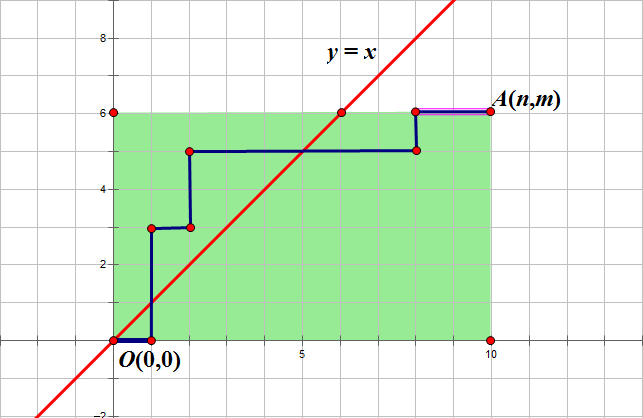
對於一個如下的網格,有這樣的一條違法路徑穿過了
易得,不能穿過
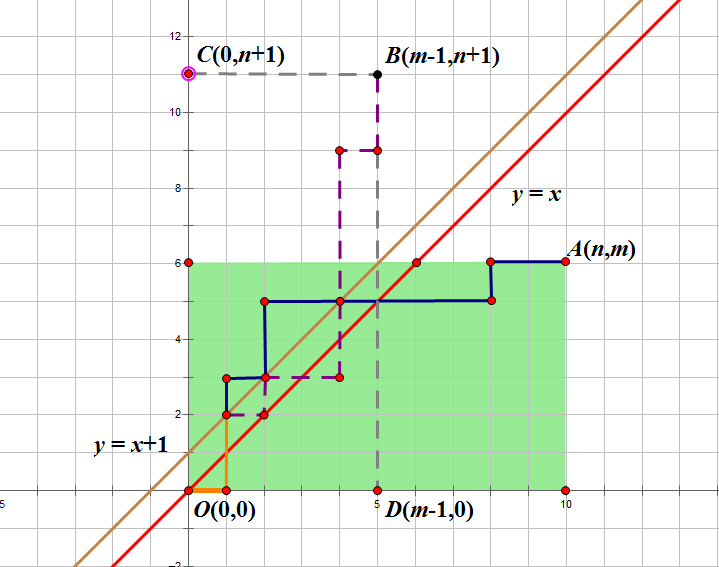
像這樣,路徑中點
所以穿過直線
網格
題目描述
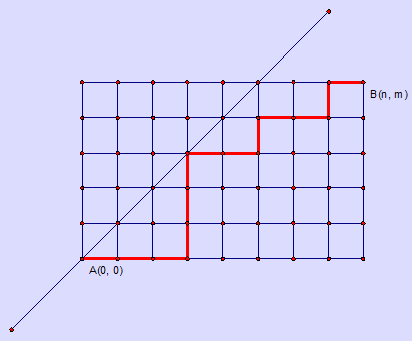
某城市的街道呈網格狀,左下角座標為AA(00,00),右上角座標為BB(nn,mm),其中nn>=mm。現在從AA(00,00)點出發,只能沿著街道向正右方或者正上方行走,且不能經過圖示中直線左上方的點,即任何途徑的點(xx,yy)
Description
某城市的街道呈網格狀,左下角座標為A(0, 0),右上角座標為B(n, m),其中n >= m。現在從A(0, 0)點出發,只能沿著街道向正右方或者正上方行走,且不能經過圖示中直線左上方的點,即任何途徑的點(x, y)都要滿足x lca 打出 房子 include 動態 合並操作 return why 以及 題目
深繪裏一直很討厭雨天。
灼熱的天氣穿透了前半個夏天,後來一場大雨和隨之而來的洪水,澆滅了一切。
雖然深繪裏家鄉的小村落對洪水有著頑固的抵抗力,但也倒了幾座老房子,幾棵老樹被連
根拔起,以及
文章目錄題目:分析:程式碼:
題目:
傳送門
分析:
根據上面的式子,我們可以得出Nx+1\frac{N}{x}+1xN+1為偶數,因為111是奇數,而奇數+奇數才等於偶數,故Nx\frac{N
文章目錄題目:分析:程式碼:
題目:
傳送門
分析:
首先,關於這道題,有個很巧妙的ACACAC方法:在AJAJAJ沒出資料前,機智的提交,即可用returnreturnreturn 000成功AC
5793. 【NOIP2008模擬】小S練跑步
(File IO): input:run.in output:run.out
Time Limits: 2000 ms Memory Limits:
目錄:
題目:
分析:
程式碼:
題目:
分析:
實際上每次操作後的答案就是2^(圖中”元”環的個數)。
元環的意思如右圖所示,(1-2-3-4-1)和(3
目錄:
題目:
分析:
程式碼:
題目:
分析:
首先,同一列中的交換隻會影響行,同一行中的交換隻會影響列。所以我們可以分開考慮行與列這兩個問題。我做題時有一個疑
目錄:
題目:
分析:
程式碼:
題目:
分析:
面我們對 a 數列的性質做一些討論。
如果(B,K)=1(B,K)=1,對於任意的 i 都有 (a[i],B) script 連通 分配 mathjax cnblogs 沒有想到 -1 str 需要 Link
https://jzoj.net/senior/#main/show/2938
Description
地主某君有一塊由2×n個柵格組成的土地,有k個
題目
一個
n
∗
m
n*m
問題
小G有n個小弟,第i個小弟有ai點攻擊力,小G有m點血量。
小J在小G找小第的時間裡去找小Z學到了膜法,他在大戰前配置了三種魔法藥水
1:複用型藥水:花費1法力值,選擇小G的攻擊力小於等於2的一個小弟讓他跟隨自己(變為自己的小弟並且攻擊力和屬於小G時一樣
題目
解題思路
50分可以直接暴力。 能用一個變數儲存的,絕對不允許用陣列!! 定址時間卡爆!!!
#
d
題目
求一個n的全排列的變成 1…n的序列 期望最少交換次數。
題解
實在想不出來,可以找規律。 其實這題不需要找規律。
方法1
第一類斯特林數靈感? hzj的第一題,序列前n-1個元素只能夠與第n個交換,想到一圈一圈地換。 這裡也是類似的,只不過任意兩個元素都可以交
題目
給定一個點數為n個圖,m條邊。 走一條邊算1步。 共有q個詢問 每個詢問中有k個點,求有多少個點可以走最多v步走到詢問中的任意一個點。 資料範圍
n
題目
鴿鴿鴿 有一個序列,有3種操作。 ①刪除最左邊的元素 ②在序列的最左邊加入一個數。 ③查詢序列中第l個數到第r個數中第k小的數。
題解
想到之前ifk通過動態樹最終狀態的dfs序將問題轉化成靜態樹問題,我打算也用類似的方法。 其實不需要。 每次刪除和插入的都是最左邊的
題目
有 n 個瓶子,它們在桌子上排成一排。第 i 個瓶子的顏色為 ci,每次操作可以選擇兩個相鄰的瓶子,消耗他們顏色的數值乘積的代價將其中一個瓶子的顏色變成另一個瓶子的顏色。 現在要讓所以瓶子的顏色都一樣,操作次數不限,但要使得操作的總代價最小。
題解
比賽時看錯題了,看成
題目
n條線段
[
l
,
r
題目
給定一個帶權無向圖。每個點都有它的顏色。定義
D
(
s
Description
給出一個n個點,m條邊的無向圖,保證無重邊自環,第i條邊的長度為
2
i
走到對稱點
走到原終點A(n,m)的路徑數相關推薦
JZOJ.3431【GDOI2014模擬】網格 解題報告
【GDOI2014模擬】網格
【GDOI2014模擬】雨天的尾巴
JZOJ 5773. 【NOIP2008模擬】簡單數學題
JZOJ 5775. 【NOIP2008模擬】農夫約的假期
JZOJ P5793. 【NOIP2008模擬】小S練跑步
JZOJ 3385. 【NOIP2013模擬】黑魔法師之門
JZOJ 3382. 【NOIP2013模擬】七夕祭
JZOJ 3384. 【NOIP2013模擬】理科男
[jzoj]2938.【NOIP2012模擬8.9】分割田地
JZOJ 5938. 【NOIP2018模擬10.30】分離計劃
JZOJ 5937. 【NOIP2018模擬10.30】斬殺計劃
JZOJ 5936. 【NOIP2018模擬10.29】逛公園
JZOJ 5931. 【NOIP2018模擬10.27】氣泡排序
JZOJ 5932. 【NOIP2018模擬10.27】情報中心
JZOJ 5933. 【NOIP2018模擬10.27】百鴿籠
JZOJ 5925. 【NOIP2018模擬10.25】naive 的瓶子
JZOJ 5919. 【NOIP2018模擬10.22】逛公園
JZOJ 5926. 【NOIP2018模擬10.25】naive 的圖
[JZOJ 5895]【NOIP2018模擬10.5】旅遊