LSTM（long short-term memory,LSTM）:長短時記憶網路，是迴圈神經網路（recurrent neural network,RNN）的一個重要結構，迴圈神經的主要用途是處理和預測序列資料。全連線神經網路（感知機，BP神經網路，RBF 神經網路等）或卷積神經網路模型中，網路結構都是從輸入層到隱含層再到輸出層，層與層之間是全連線或部分連線，每層節點之間是無連線的。然而迴圈神經網路為了刻畫一個序列的當前的輸出資訊和之前資訊的關係。從結構上說，迴圈神經網路會記憶之前的資訊，並利用之前記憶的資訊影響後面節點的輸出。迴圈神經網路的隱藏層之間的節點是有連線的，隱藏層的輸入不僅包括輸入層的輸出，還包括上一時刻隱藏層的輸出。 

網路的具體結構以及意義，參考下文

下面是我的資料預測：

# -*- coding: utf-8 -*-
"""
 LSTM prediction
@author: ljq

"""
#匯入庫函式
import numpy 
import matplotlib.pyplot as plt
from pandas import read_csv
import math
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import mean_squared_error
#讀取資料
data= read_csv('data_s.csv') #csv檔案 n*1 ,n代表樣本數，反應時間序列，1維資料
values1 = data.values;
dataset=values1[:,0].reshape(-1,1)#注意將一維陣列，轉化為2維陣列
dataset = dataset.astype('float32')#將資料轉化為32位浮點型，防止0資料 
                  
# convert an array of values into a dataset matrix
def create_dataset(dataset, look_back=1):#後一個數據和前look_back個數據有關係
    dataX, dataY = [], []
    for i in range(len(dataset)-look_back-1):
        a = dataset[i:(i+look_back), 0]
        dataX.append(a) #.apeend方法追加元素
        dataY.append(dataset[i + look_back, 0])
    return numpy.array(dataX), numpy.array(dataY) #生成輸入資料和輸出資料 

numpy.random.seed(7)#隨機數生成時演算法所用開始的整數值


# normalize the dataset
scaler = MinMaxScaler(feature_range=(0, 1))#歸一化0-1
dataset = scaler.fit_transform(dataset)
# split into train and test sets  #訓練集和測試集分割
train_size = int(len(dataset) * 0.67)#%67的訓練集，剩下測試集
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]#訓練集和測試集

# use this function to prepare the train and test datasets for modeling
look_back = 1
trainX , trainY = create_dataset(train, look_back)#訓練輸入輸出
testX,testY=create_dataset(test, look_back)#測試輸入輸出


 #reshape input to be [samples, time steps, features]#注意轉化資料維數
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1]))

#建立LSTM模型
model = Sequential()
model.add(LSTM(11, input_shape=(1, look_back)))#隱層11個神經元 （可以斷調整此引數提高預測精度）
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')#評價函式mse，優化器adam
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)#100次迭代 
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
#資料反歸一化
trainPredict = scaler.inverse_transform(trainPredict)
trainY = scaler.inverse_transform([trainY])
testPredict = scaler.inverse_transform(testPredict)
testY = scaler.inverse_transform([testY])

trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))


trainPredictPlot = numpy.empty_like(dataset)
trainPredictPlot[:, :] = numpy.nan
trainPredictPlot[look_back:len(trainPredict)+look_back, :] = trainPredict

# shift test predictions for plotting
testPredictPlot = numpy.empty_like(dataset)
testPredictPlot[:, :] = numpy.nan
testPredictPlot[len(trainPredict)+(look_back*2)+1:len(dataset)-1, :] = testPredict

# plot baseline and predictions

plt.figure(figsize=(20,6))
l1,=plt.plot(scaler.inverse_transform(dataset),color='red',linewidth=5,linestyle='--')
l2,=plt.plot(trainPredictPlot,color='k',linewidth=4.5)
l3,=plt.plot(testPredictPlot,color='g',linewidth=4.5)
plt.ylabel('Height m')
plt.legend([l1,l2,l3],('raw-data','true-values','pre-values'),loc='best')
plt.title('LSTM Gait Prediction')
plt.show()
 

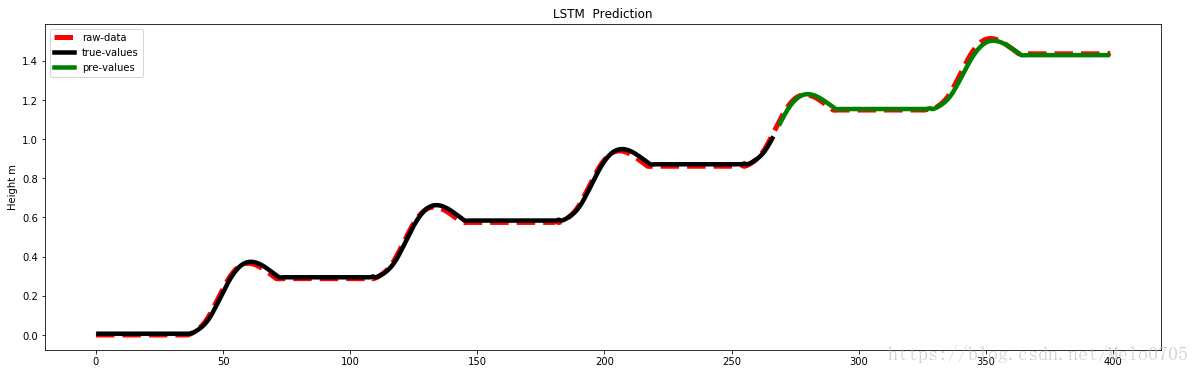
以下是實驗結果：

下面介紹程式中的一些用法及註釋：

Pandas資料匯入：可參考官方文件 ：

#舉一個簡單的例子 用一下pandas讀資料

import pandas as pd
 #Read data
data = pd.read_excel(r'C:\Users\1042zyl\Desktop\pptdata.xlsx',sheet_name=3,index_col = None)
#Normalization 規範化量程在0-1
data = (data - data.min()) / (data.max() - data.min())
#Export excel
data.to_excel('1.xlsx')

batch_size 大小選擇

numpy中的: 物件.shape():讀取物件的維度。物件.shape(0)讀取行數;  物件.shape(1)讀取列數,。注意list（列表）是沒有shape屬性的，需要把它轉化為    np.shape(x)或者np.arrray(x).shape.  擴充套件：numpy 中轉置：np.transpose(x)或者np.arrray(x).T

注意這裡的np.array（x）只是將資料化成numpy要求，維度並沒有變化。

numpy 中的reshape用法參考官網

對其中的一句做解釋，One shape dimension can be -1. In this case, the value is inferred from the length of the array and remaining dimensions.-1代表不確定數，當行數不確定[-1,1];當列數不確定[1,-1]

注意設定.reshape(資料，newspace=（行數，k個1，列數）) 可以實現增加維數。