35. 排序演算法(8):歸併排序的迭代實現
阿新 • • 發佈:2019-02-13
1. 基本原理
在上篇文章中介紹了歸併排序的遞迴實現,雖然遞迴的實現方式很簡單,通過遞迴呼叫就可以實現,但是會佔用大量的時間和空間,使得演算法的效率下降;使用迭代的方式代替遞迴的方式雖然會使得程式碼的編寫變得困難,但是會增大效率。
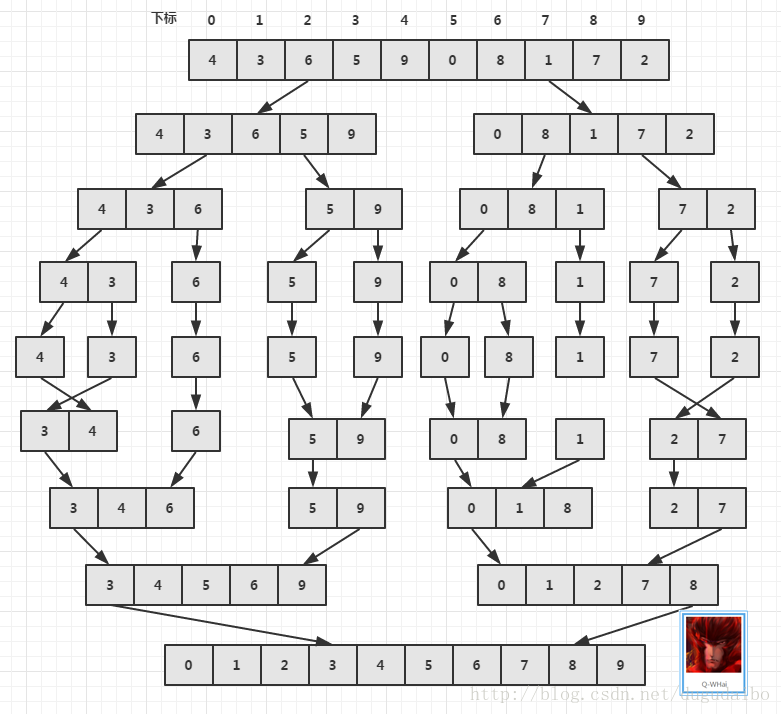
遞迴的思想實際上是從上往下“遞”,再從下往上“歸”。遞迴的實現過程可以看成如下的過程
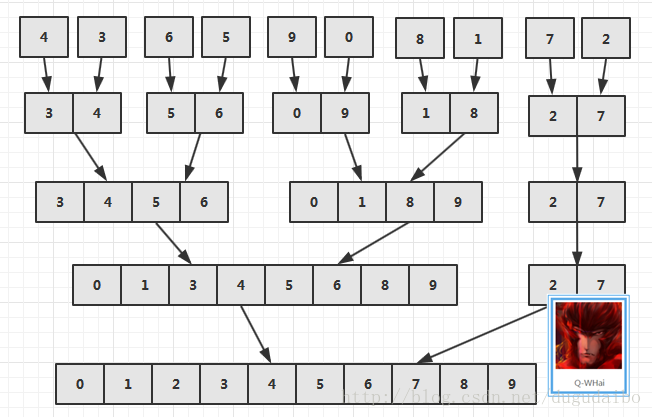
而迭代的過程就是化成一個個小的排序問題,再合併到一起,比如如下的過程
2. 程式碼實現
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 10
void MergeSort(int