最近在惡補一些計算機基礎內容，看到了堆排序，想想以前常說堆疊堆疊，但我竟然連堆有哪些應用都記不得了，所以，重溫了堆排序後，我來給大家分享一下，希望能對大家有所幫助。（程式碼實現不採用虛擬碼，使用java實現，畢竟來看部落格的都不想和看書一樣把）

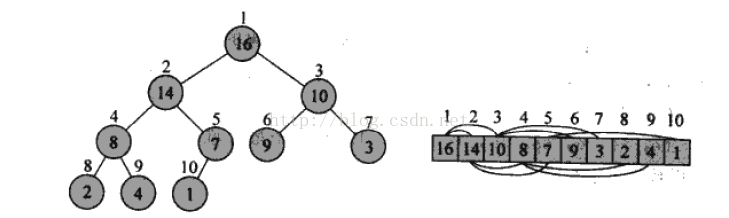
       首先，堆是一種資料結構，你可以把他看成一顆完全二叉樹，如下圖所示：圓圈上方的數字代表下標：他的特性就是：父結點的值要大於兩個兒子結點的值。

        上圖選自演算法導論，下標從1開始，但我們寫的時候，肯定是要按照從0開始的下標來寫程式碼拉，這一點後面不會再特別說明了。

        雖然堆可以用陣列表示，但堆和陣列有所區別，主要是在於陣列的長度（length）不一定等於堆的大小（heapSize）。heapSize <= length。下標大於heapSize但小於length的值都不屬於堆結構。

        所以，在java裡先新建一個類來表示堆：沒有使用陣列的原因是，java裡陣列初始化以後就不能再新增元素了，在講解後面內容的時候會有所不方便。

    public class Heap {  
      
        private ArrayList<Integer> A;  
      
        private int heapSize;  
      
        public ArrayList<Integer> getA() {  
            return A;  
        }  
      
        public void setA(ArrayList<Integer> a) {  
            A = a;  
        }  
      
        public int getHeapSize() {  
            return heapSize;  
        }  
      
        public void setHeapSize(int heapSize) {  
            this.heapSize = heapSize;  
        }  
          
    } 
 

很容易得知，結點i的左兒子右兒子或父結點的下標的計算函式

// 左節點下標
    public int left(int i) {
        return i * 2 + 1;
    }

    // 右節點下標
    public int right(int i) {
        return i * 2 + 2;
    }

    // 父節點下標
    public int parent(int i) {
        return (i - 1) / 2;
    }

要實現堆排序，我們首先得保持堆的性質。（下面用最大堆舉例）

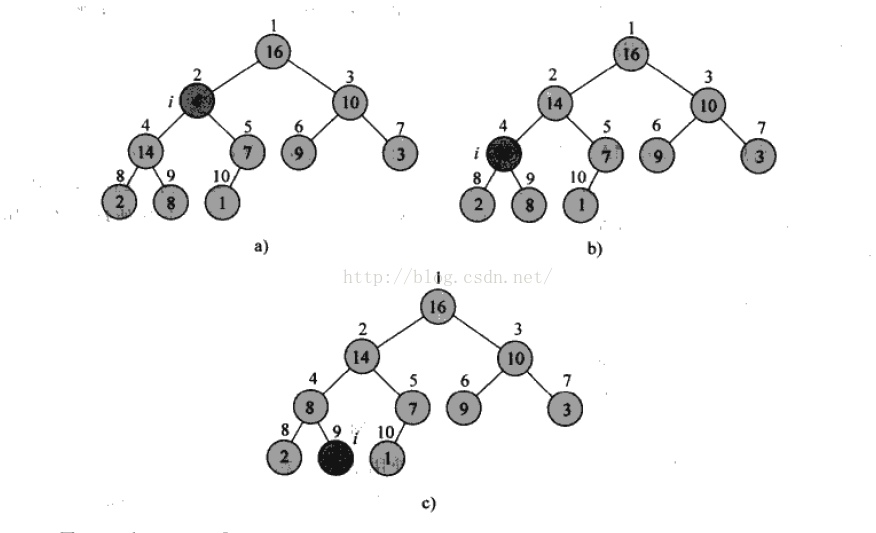
      當兒子結點大於父節點的時候，就失去了最大堆的性質，所以在這個時候，我們只要把兒子結點和父結點交換，但是交換以後，被交換的父結點的兒子結點發生了變化，可能會繼續違背最大堆這個性質，所以要遞迴呼叫這個演算法。過程大致如下圖所示：

對2號結點進行最大堆性質的保持

        要實現這個過程的程式碼如下：

   /**
     * 遞迴實現的堆排序
     * @param heap 堆
     * @param i 當前座標
     */
    public void MaxHeapify(Heap heap, int i) {
        int l = left(i);
        int r = right(i);
        int largest = i;
        if (l < heap.getHeapSize() && heap.getA().get(l) > heap.getA().get(i)) {
            largest = l;
        }
        if (r < heap.getHeapSize() && heap.getA().get(r) > heap.getA().get(largest)) {
            largest = r;
        }
        if (largest != i) {
            int temp = heap.getA().get(i);
            heap.getA().set(i, heap.getA().get(largest));
            heap.getA().set(largest, temp);
        } else
            return;
        MaxHeapify(heap, largest);
    }

其實，這個演算法是可以非遞迴實現的，可以提升效率：

/**
     * 非遞迴實現的堆排序
     * @param heap 堆
     * @param i 當前座標
     */
    public void MaxHeapifyNoRecursive(Heap heap, int i) {
        while (true) {
            int l = left(i);
            int r = right(i);
            int heapSize = heap.getHeapSize();
            ArrayList<Integer> A = heap.getA();
            int largest = i;
            if (l < heapSize && A.get(l) > A.get(i)) {
                largest = l;
            }
            if (r < heapSize && A.get(r) > A.get(largest)) {
                largest = r;
            }
            if (largest != i) {
                int temp = A.get(i);
                A.set(i, A.get(largest));
                A.set(largest, temp);
            } else
                return;
            i = largest;
        }
    }

有了上述的演算法，我們就可以進行建堆操作了，建堆的過程很簡單，從下標heapSize - 1開始，對每個結點都執行MaxHeapify就行了，但是葉子結點由於沒有子結點，所以只需要從（heapSize - 1）/2開始，對每個結點都執行MaxHeapify就行了

/**
     * 構建最大堆
     * @param heap 堆
     */
    public void BuildMaxHeap(Heap heap) {
        int heapsize = heap.getHeapSize();
        for (int i = (heapsize - 1) / 2; i>= 0; i--) {
            MaxHeapify(heap, i);
        }
    }

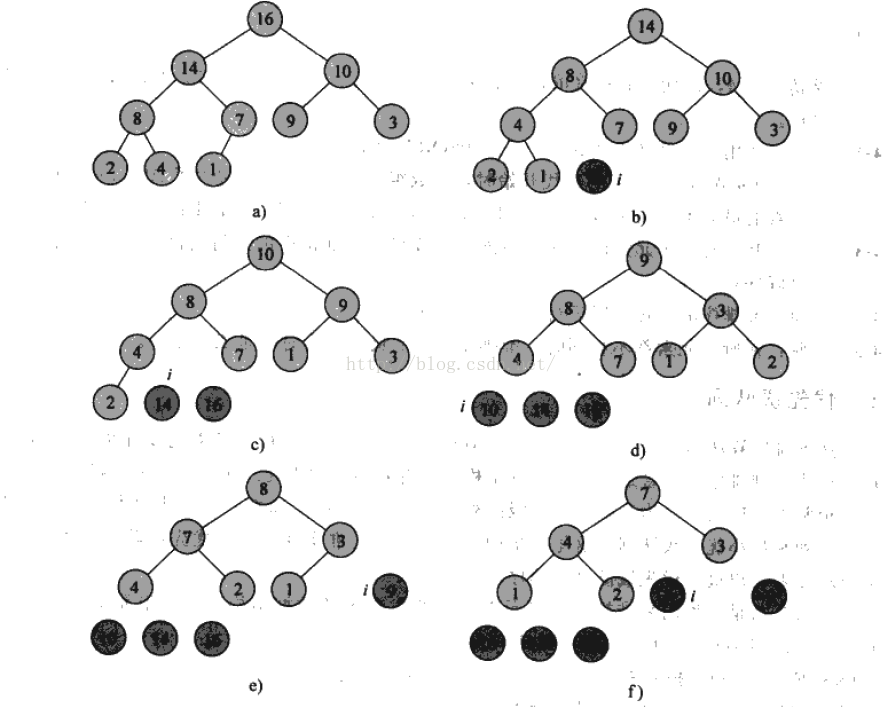
這個過程大概如下圖所示：

接下來，就是堆排序演算法了。

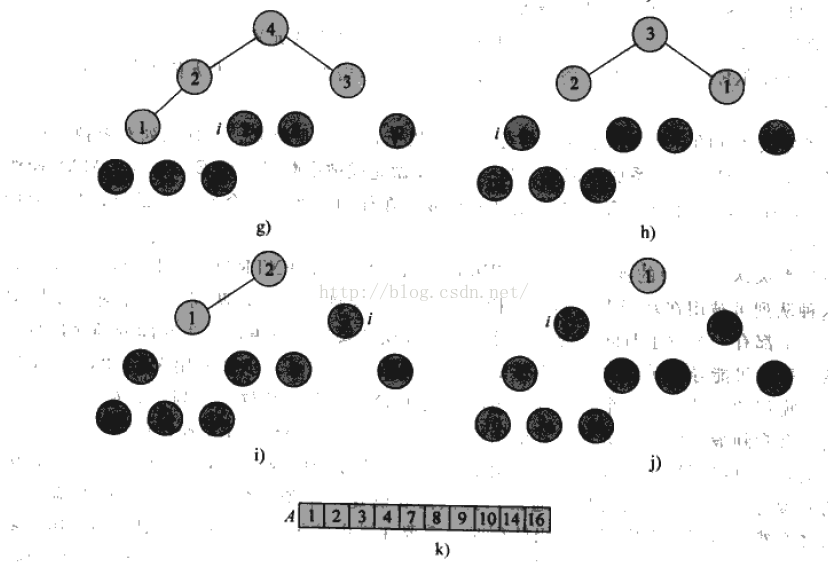
先用BuildMaxHeap把輸入的陣列A構造成最大堆。然後，把下標heapSize - 1的元素和下標為0的元素對換，通過減小heapSize，讓下標為heapSize - 1的元素從堆中剔除，再呼叫MaxHeapify（heap, 0）即可保證最大堆的性質。重複這個過程，直到堆中只剩下一個元素。

/**
     * 堆排序演算法
     * @param heap 堆
     */
    public void HeapSort(Heap heap) {
        BuildMaxHeap(heap);
        int length = heap.getA().size(), heapSize = heap.getHeapSize();
        for (int i = length - 1; i > 0; i--) {
            int temp = heap.getA().get(i);
            heap.getA().set(i, heap.getA().get(0));
            heap.getA().set(0,temp);
            heap.setHeapSize(--heapSize);
            MaxHeapify(heap, 0);
        }
    }

這個過程的圖示如下：

這樣堆排序演算法就算完成了，複雜度僅為O(nlg(n))，但是，其實快速排序往往優於它，雖然複雜度和它一樣。
如果有啥問題記得跟我說哈

原文：http://blog.csdn.net/qj30212/article/details/52443250

我略微修改了一下程式碼和描述