簡介

字尾三姐妹：字尾陣列，字尾自動機，字尾樹。
字尾自動機：Suffix Automation，也叫SAM。
創立演算法的思路來源：能不能構出一個自動機（本質就是一個有向圖），能識別一個串的所有後綴。

識別所有後綴基礎想法

把所有的字尾都放進一個trie裡面，比如串aabbabd。

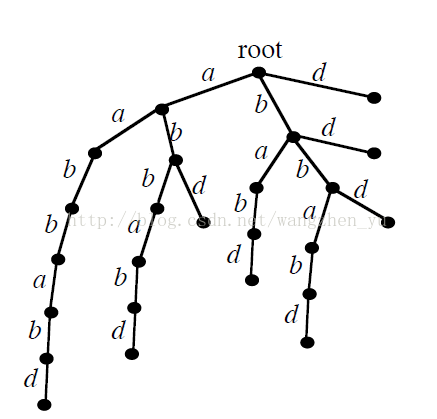
這樣的狀態太多了，怎麼把狀態數縮小。

減小狀態數的方法

定義一個子串的right集合為這個子串在原串中出現的右端點集合。
如果兩個子串A和B的right集合完全相同的話，那麼他們明顯一個是另一個的字尾，假設A是B的字尾，那麼他們再繼續擴充套件都只會是同一種狀態，所以可以把他們合併為同一種狀態。
其實字尾自動機就像是一個維護right集合的關係的一個自動機。
怎麼處理呢？下面會說。先看一些重要的變數。

重要的變數

先放個圖。

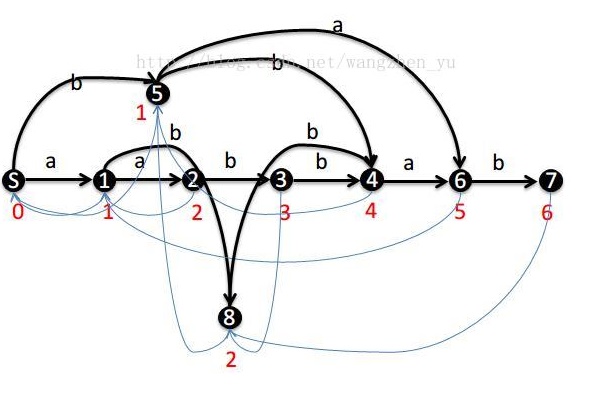
這個就是aabbab的字尾自動機。
標有數字的是狀態節點。
設S狀態（節點）為初始狀態，表示一個空串。S節點到達任意一個節點的任意一條路徑都可以形成一個字串，且這個字串與其他形成的字串不同。
每個點都有一些值：len,fa,son[26]。（這裡的字母都只考慮小寫字母,用0…25表示小寫字母）
∙1先來看看len是什麼：觀察上面的圖，每個節點的len是這個狀態（節點）表示的最大字串的長度，一個狀態表示的所有字串就是S到達這個節點形成的所有字串。上圖中的len[0…8]=0,1,2,3,4,1,6,7,2。
∙2再來看看son[26]是什麼：從一個節點x走c字元，走到了節點y，那麼son[x][c]=y。但是為什麼son[x][c]只連向y這個點不連向其他的點？這樣連有什麼性質嗎？回顧上面的《減小狀態數的方法》，如果兩個狀態的right集合相同那麼可以合併為一種狀態，現在這裡的x狀態表示的所有字串加了個c之後right集合和y的right集合完全一樣

，所以son[x][c]=y，就相當於把兩個狀態合併了。觀察上面所有節點，每個節點可能會有好幾條連向來的邊，這樣導致這個節點會表示好多字串，但是這些字串的right集合都是一樣的。
∙3網上很多都說的是這個節點可以接受新的字尾，fa[x]返回上一個可以接受新字尾的節點，怎麼都看不懂？後來直接去看論文才搞懂。其實fa[x]的right集合是包含x的right集合的且要保證fa[x]的right集合儘量的小。因為right集合儘量小就與x的right集合更接近，如果x向後擴展出一個新的字元構成的狀態y（新的字尾），fa[x]的right集合因為包含x的right集合，那麼fa[x]也可以擴展出這個新的字元並構成新的狀態，這個狀態可能會與y合併，這就是下面要講的字尾自動機的構造。

parent樹的一些性質

∙1：從葉子節點向上走就是right集合不斷合併的過程
∙2：設一個狀態最短串為mins，最長串為maxs=lens，那麼mins-1=max_fa[s]
∙3：網上說的接受字尾，其實可以換一種好理解的說法，parent的樹從下到上right集合不斷變大其實就是不斷尋找字尾的過程

字尾自動機的構造

當前字串S構建了i-1個點。
設表示S[1…i-1]的節點是last，現在要構建第i個節點，建出新的狀態np，那麼很明顯len[np]=i=len[last]+1。設p=last

    p=last,np=++num;
    t[np].len=t[p].len+1;

那麼現在要合併狀態了，現在已經把p擴展出的s[i]字元的狀態和np狀態合併了，那麼因為fa[p]的right集合包含了p的right集合，所以fa[p]擴展出s[i]這個字元的狀態可能會與np合併。
什麼情況下才會合並，如果son[p][s[i]]=0,那麼加上了s[i]字元的狀態，在當前狀態的自動機下它right集合肯定只有i，因為s[i]是新出現的，所以加上新出現的right集合肯定只有i。然後fa[p]肯能也沒有s[i]節點，fa[fa[p]]可能也沒有s[i]，所以一直找到p=0或p有s[i]節點。

while(p&&!t[p].son[c])t[p].son[c]=np,p=t[p].fa;

為了方便，我們沒有零號節點，空串用1號節點表示。
如果p=0的話，就說明已經走過了空串狀態（1號節點），但是空串的right集合肯定是包括np的right集合的，所以t[np].fa=1

 if(!p)t[np].fa=1;

如果p不等於0，就說明p現在有s[i]這個節點，設p走s[i]走到的節點為q。
現在就有兩種情況了
（強行把s[i]加入q可能會使t[q].len變小，而且藍色的串不能直接放入加上X字元的集合，因為會與字元B衝突如圖）：

1、t[p].len+1=t[q].len，說明p表示的最長字串和q表示的最長字串只差了一位（就是s字串走到第j個得到狀態p，走到第j+1個得到狀態q），現在p的right集合是包含last的right集合的，但是last走s[i]字元擴展出np，p走s[i]字元擴展出q，那麼q的right肯定也是包含np的right。
2、t[p].len+1< t[q].len(t[p].len+1!=t[q].len)現在多加了一個s[i]，在這種情況q代表的串中，長度不超過t[p].len+1的字串的right集合會多一個i超過t[p].len+1的字串因為與p表示的最長字串差了好幾位，這些字串的right集合明顯不會增加。那麼現在就要把狀態拆開了。
新建一個節點nq，因為nq只是從q拆出來的，那麼他的son和fa都是和q相等的，只是用len來拆開，len[nq]=len[p]+1。現在nq的right多了一個i，肯定包括q和np的right而且還儘量的小。
然後前面原來狀態與q合併的點，他們的right集合都會多一個i，所以要他們與nq合併。
然後字尾自動機就構造完了。

else{
        q=t[p].son[c];
        if(t[p].len+1==t[q].len)t[np].fa=q;
        else{
            nq=++num;
            t[nq]=t[q];
            t[num].len=t[p].len+1;
            t[q].fa=t[np].fa=nq;
            while(p&&t[p].son[c]==q)t[p].son[c]=nq,p=t[p].fa;
        }
    }

字尾自動機的運用

現說幾個字尾自動機的性質：
1、每個狀態i的點表示的字串長度的範圍是(len[fa[i]]…len[i]]。(從len[fa[i]]+1…len[i])
2、每個狀態i表示的所有字串的出現次數和right集合都是一樣的。
3、由fa構成的數叫做parent樹，parent樹上子節點的right是父節點的子集。
4、字尾自動機的parent樹是原串的反向字首樹，那麼也是原串的反串的字尾樹。
5、兩個串的最長公共字尾是在後綴自動機上對應的狀態在parent樹上的lca的狀態。

兩個串的最長公共子串

建出A串的字尾自動機，然後B串在後綴自動機上跑。

找不同的子串的個數

方法一：用dfs處理處每個點能擴展出多少個字串sum[x]=∑sum[t[x].son[i]]+1，其實可以不用dfs，拓撲一下（按len從小到大）然後倒著做。最後sum[1]就是所有子串的個數。
方法二：ans=∑t[x].len−t[t[x].fa].len，這裡運用了性質1，因為節點i表示的字串大小範圍是從len[fa[i]]+1…len[i]的，那麼包含不同串的個數=len[i]−(len[fa[i]]+1)+1=len[i]−len[fa[i]]

找第K大的子串

1、找不同串的第K大：預處理出每個狀態可以構出多少個字串，可以用dfs做，也可以對自動機拓撲一下（其實就相當於把len從小到大排序，因為len小的拓撲序也會小），然後倒著求一下（相當於DAG上的DP），然後dfs去找第K大的就好了。
2、找相同串的第K大：除了要預處理出上面的東西，還要預處理出所有狀態right集合的大小（每個串在原串中出現多少次），這個會影響上面的要求的值，然後在做dfs的時候同時處理一下就好了。
原題TJOI2015弦論

求最小迴圈表示

最小迴圈表示就是這個串的所有迴圈串中的字典序最小的串。
把原串複製一遍到後面，然後建立字尾自動機，每次當前連出走字典序最小的點，一直走到長度為|S|為止。

找回文串

構造原串的字尾自動機，求出每個節點right集合的rmax，然後把反串放到字尾自動機上面執行，如果當前的匹配串在原串中的範圍[l…r]覆蓋了當前節點的rmax，那麼[l…rmax]就是一個迴文串。

Trie上建SAM

看起來很高階的樣子，其實就是每個節點的last就是trie上的父節點。為什麼要在trie上建呢？
比如說要把很多個串同時建立字尾自動機，那麼有兩種方法：
方法一：把所有的字串都用一個與眾不同的字元隔起來，然後建立字尾自動機。
方法二：把所有的字串放到一個trie上，然後在trie上建立字尾自動機。（其實這個好像也叫廣義字尾自動機）

總結

其實字尾陣列能幹的很多事情都可以用字尾自動機來幹，字尾自動機因為有樹形結構所以加上了樹鏈剖分可以用很多資料結構來維護，它的程式碼簡介，常數又小，速度又快，但是需要多加思考才能解決題目。

由於本人是一個蒟蒻

對於字尾自動機知道的也只有這麼多了。

推薦題目