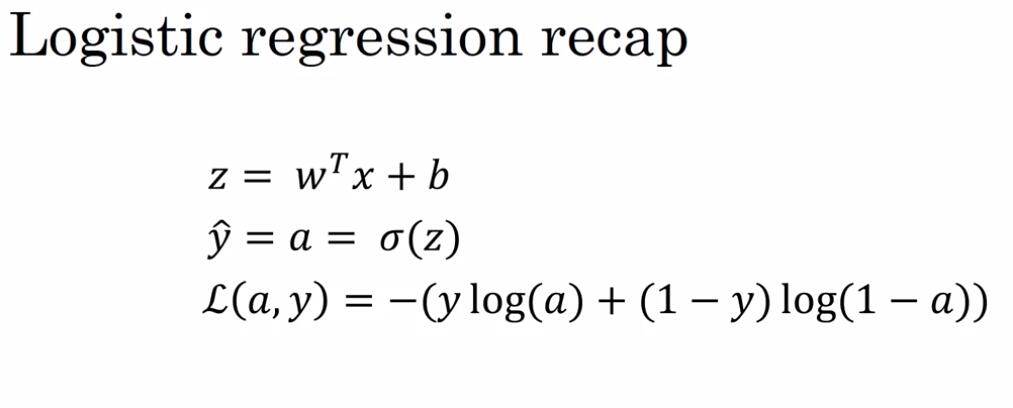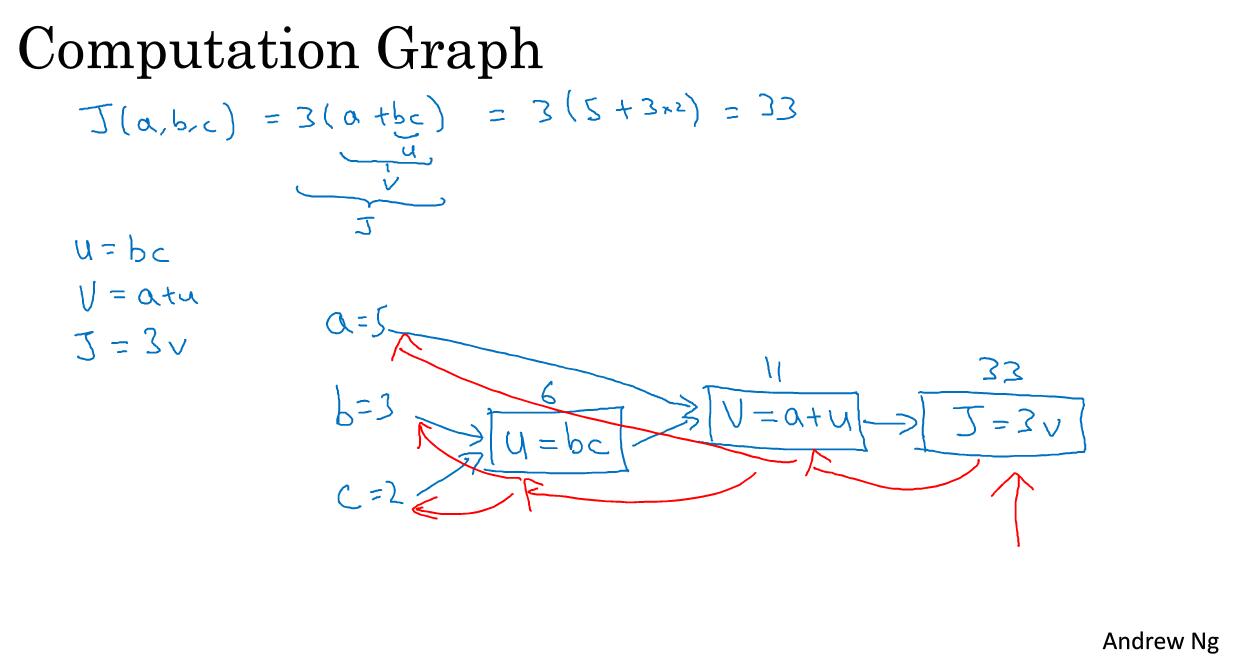
計算圖

可以說，一個神經網路的計算都是按照前向或者反向傳播過程來實現的，首先計算出神經網路的輸出，緊接著一個反向傳播的操作。後者，我們用來計算出對應的梯度或者導數。這個流程圖解釋了為什麼用這樣的方式來實現。

我們舉一個更為簡單的函式為例，如何計算該函式。具體流程如下：

流程圖是用藍色箭頭畫出來的，從左到右的計算過程。那麼紅色箭頭是從右到左的導數計算過程。

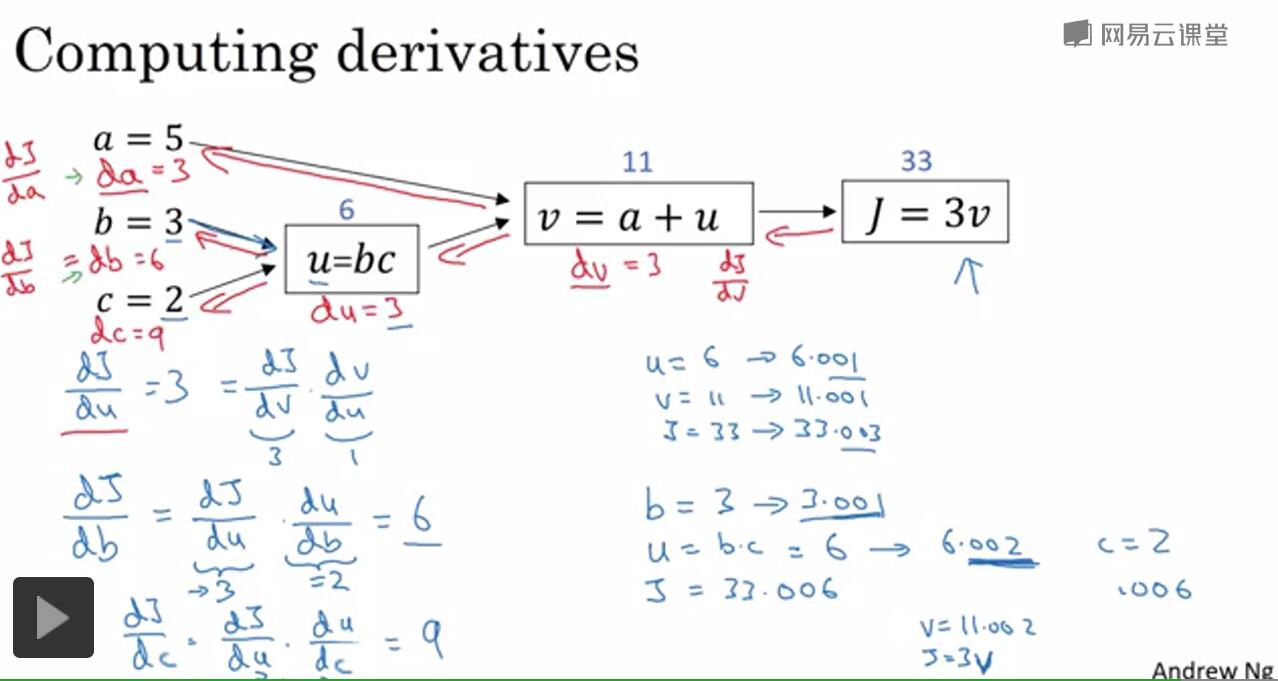
計算圖的導數計算

反向傳播演算法的實質實際上就是用微積分的鏈式法則求導的過程。

比如說我們算dJ/da的大小，就用鏈式法則反過來算一下。

logistic迴歸的梯度下降法

這一部分將介紹如何用導數流程圖來計算梯度。

我們回憶一下邏輯迴歸公式，注意這裡的a是預測值的意思等於y(i)

整個計算流程如圖

想要計算損失函式L的導數，要逐步返回計算前面各項的導數。

如圖所示，我們先用反向傳播方法求出各個導數值（對於單個變數的就是這麼算），然後使用梯度演算法，更新

m個樣本的梯度下降

之前我們介紹瞭如何將梯度迴歸應用到Logistic迴歸的一個訓練樣本上，現在我們想要把他們應用到m個訓練樣本上。

首先，我們要明確成本函式J(w,b)，期望使得成本函式達到最小的值。

如圖所示，我們這裡要做的就是使用之前的鏈式法則求出相應的導數值，做差，然後求平均。這就是Logistic迴歸和梯度下降演算法。

整個計算的程式設計流程如下：

完成左側的迭代計算之後，我們使用梯度演算法對w進行一次學習更新（寫在右側），即w1減去學習率乘以dw1。然後不斷重複這些步驟，即迭代完成之後進行更新

注意這裡我們每一個xi都會計算出一個dw，而我們希望得到的是dw的平均值，所以最後除以m。當我們用向量化進行計算也是一樣的，對於所有的X也就是X向量，除以m取一個平均值。