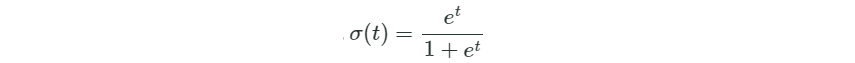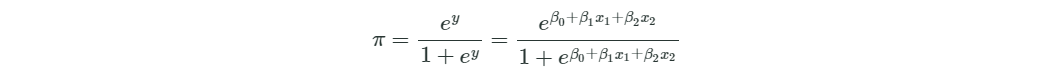Dataset

每年高中生和大學生都會申請進入到各種各樣的高校中去。每個學生都有一組唯一的考試分數，成績和背景資料。錄取委員會根據這個資料決定是否接受這些申請者。在這種情況下一個二元分類演算法可用於接受或拒絕申請，邏輯迴歸是個不錯的方法。

• 資料集admissions.csv包含了1000個申請者的資訊，特徵如下：

gre - Graduate Record Exam（研究生入學考試）, a generalized test for prospective graduate students（一個通用的測試未來的研究生）, continuous between 200 and 800.
gpa

- Cumulative grade point average（累積平均績點）, continuous between 0.0 and 4.0.
admit - Binary variable, 0 or 1, where 1 means the applicant was admitted to the program.

Use Linear Regression To Predict Admission

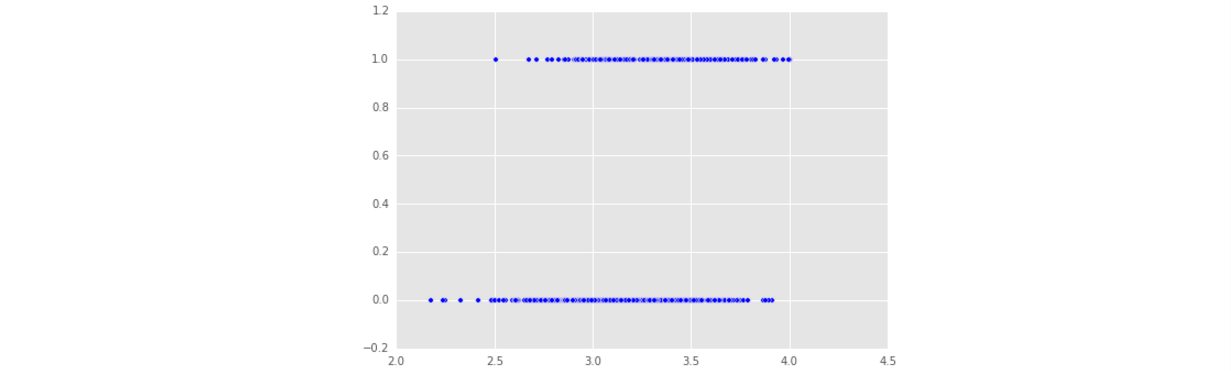
• 這是原本的資料，admit的值是0或者1。可以發現”gpa”和”admit”並沒有線性關係，因為”admit”只取兩個值。

import pandas
import matplotlib.pyplot
 
 as plt
admissions = pandas.read_csv("admissions.csv")
plt.scatter(admissions["gpa"], admissions["admit"])
plt.show()

• 這是通過線性迴歸模型預測的admit的值，發現admit_prediction 取值範圍較大，有負值，不是我們想要的。

# The admissions DataFrame is in memory

# Import linear regression class
from sklearn.linear_model import LinearRegression

# Initialize a linear regression model
model = LinearRegression()

# Fit model
model.fit(admissions[['gre', 'gpa']]
 
, admissions["admit"])

# Prediction of admission
admit_prediction = model.predict(admissions[['gre', 'gpa']])

# Plot Estimated Function
plt.scatter(admissions["gpa"], admit_prediction)

• 因此我們期望構造一個模型，能夠給我們一個接受（admission）的概率，並且這個概率取值在[0~1]，然後我們根據銀行信用卡批准——模型評估ROC&AUC這篇文章的方法來選擇合適的閾值進行分類。

The Logit Function

邏輯迴歸是一個流行的分類方法,它將輸出限制在0和1之間。這個輸出可以被視為一個給定一組輸入某個事件的概率,就像任何其他分類方法。

• logit function是邏輯迴歸的基礎，這個函式的形式如下：

  

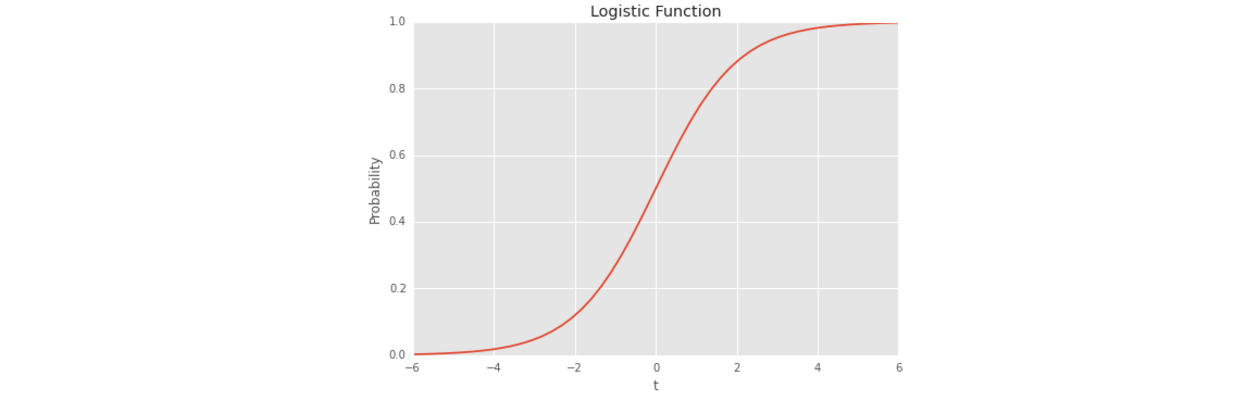
• 觀察一下logit function的樣子：

# Logistic Function
def logit(x):
    # np.exp(x) raises x to the exponential power, ie e^x. e ~= 2.71828
    return np.exp(x) / (1 + np.exp(x)) 

# Linspace is as numpy function to produced evenly spaced numbers over a specified interval.
# Create an array with 50 values between -6 and 6 as t
t = np.linspace(-6,6,50, dtype=float)

# Get logistic fits
ylogit = logit(t)

# plot the logistic function
plt.plot(t, ylogit, label="logistic")
plt.ylabel("Probability")
plt.xlabel("t")
plt.title("Logistic Function")
plt.show()
a = logit(-10)
b = logit(10)
'''
a:4.5397868702434395e-05
b:0.99995460213129761
'''

The Logistic Regression

• 邏輯迴歸就是將線性迴歸的輸出當做Logit Function的輸入然後產生一個輸出當做最終的概率。其中β0是截距，其他的βi是斜率，也是特徵的係數。
  
• 與線性模型一樣，我們想要找到最優的βi的值使得預測值與真實值之間的誤差最小。通常用來最小化誤差的方法是最大似然法和梯度下降法。

Model Data

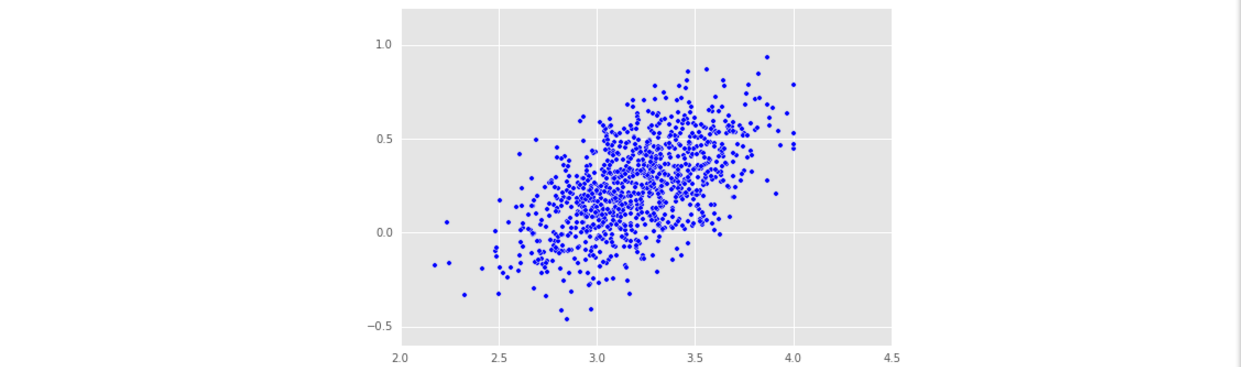
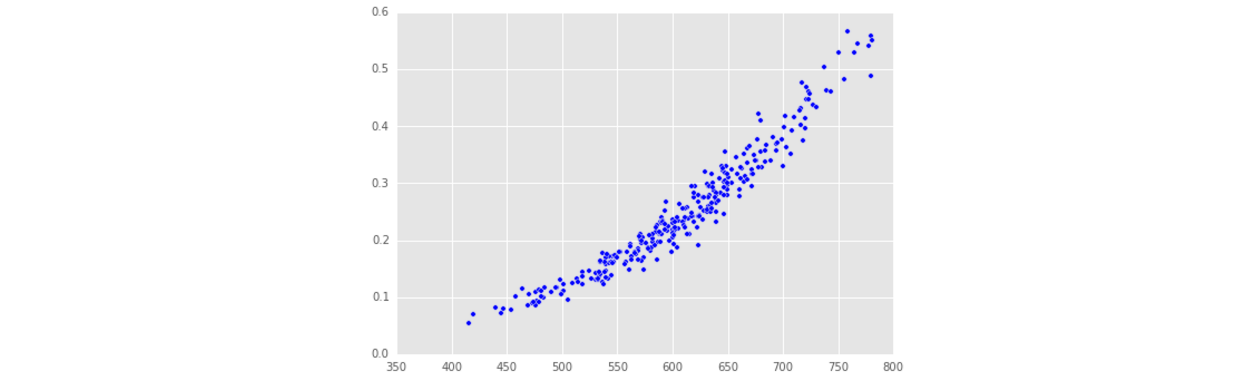
• 下面進行邏輯迴歸實驗，每次進行訓練測試集劃分之前，需要將樣本資料進行洗牌，這樣抽樣具有隨機性。看到最後的gre和預測值的關係發現，當gre越大時，被接受的概率越大，這是符合實際情況的。

from sklearn.linear_model import LogisticRegression

# Randomly shuffle our data for the training and test set
admissions = admissions.loc[np.random.permutation(admissions.index)]

# train with 700 and test with the following 300, split dataset 
num_train = 700
data_train = admissions[:num_train]
data_test = admissions[num_train:]

# Fit Logistic regression to admit with gpa and gre as features using the training set
logistic_model = LogisticRegression()
logistic_model.fit(data_train[['gpa', 'gre']], data_train['admit'])

# Print the Models Coefficients
print(logistic_model.coef_)
'''
[[ 0.38004023  0.00791207]]
'''

# Predict the chance of admission from those in the training set
fitted_vals = logistic_model.predict_proba(data_train[['gpa', 'gre']])[:,1]
fitted_test = logistic_model.predict_proba(data_test[['gpa', 'gre']])[:,1]

plt.scatter(data_test["gre"], fitted_test)
plt.show()

Predictive Power

• 這裡有個用法需要提一下，accuracy_train = (predicted == data_train[‘admit’]).mean()中predicted == data_train[‘admit’]得到是一個布林型array,在計算mean()時，會將True記作1，False記作0，然後求均值。但是在list中是不行的，list物件的布林型資料沒有mean()這個函式。

# .predict() using a threshold of 0.50 by default
predicted = logistic_model.predict(data_train[['gpa','gre']])

# The average of the binary array will give us the accuracy
accuracy_train = (predicted == data_train['admit']).mean()

# Print the accuracy
print("Accuracy in Training Set = {s}".format(s=accuracy_train))
'''
# 這種輸出方式也很好
Accuracy in Training Set = 0.7785714285714286
'''
# Percentage of those admitted
percent_admitted = data_test["admit"].mean() * 100

# Predicted to be admitted
predicted = logistic_model.predict(data_test[['gpa','gre']])

# What proportion of our predictions were true
accuracy_test = (predicted == data_test['admit']).mean()

• sklearn中的邏輯迴歸的閾值預設設定為0.5

Admissions ROC Curve

• 邏輯迴歸中的predict_proba這個函式返回的不是類標籤，而是接受的概率，這可以允許我們自己修改閾值。首先我們需要作出它的ROC曲線來觀察合適閾值：

from sklearn.metrics import roc_curve, roc_auc_score

# Compute the probabilities predicted by the training and test set
# predict_proba returns probabilies for each class.  We want the second column
train_probs = logistic_model.predict_proba(data_train[['gpa', 'gre']])[:,1]
test_probs = logistic_model.predict_proba(data_test[['gpa', 'gre']])[:,1]
# Compute auc for training set
auc_train = roc_auc_score(data_train["admit"], train_probs)

# Compute auc for test set
auc_test = roc_auc_score(data_test["admit"], test_probs)

# Difference in auc values
auc_diff = auc_train - auc_test

# Compute ROC Curves 
roc_train = roc_curve(data_train["admit"], train_probs)
roc_test = roc_curve(data_test["admit"], test_probs)

# Plot false positives by true positives
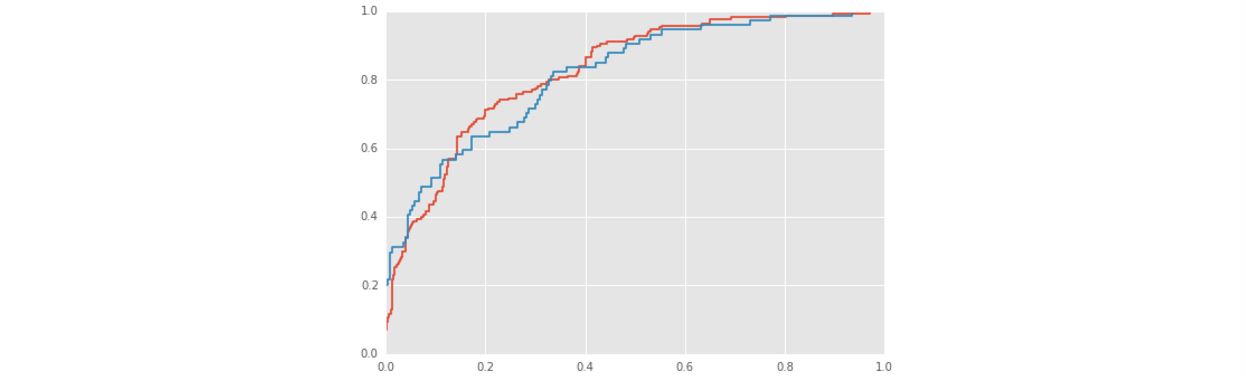
plt.plot(roc_train[0], roc_train[1])
plt.plot(roc_test[0], roc_test[1])

可以看到ROC曲線開始非常的陡峭，慢慢地變得平緩。測試集的AUC值是0.79小於訓練集的AUC值0.82，沒有過擬合.這些跡象表明我們的模型可以根據gre和gpa來預測是否錄取了。
我們也可以通過銀行信用卡批准——模型評估ROC&AUC這篇文章中提到的精確度，查準率，查全率等度量標準來衡量模型的好壞。