Dijkstra演算法是由荷蘭電腦科學家狄克斯特拉（Dijkstra）於1959 年提出的，因此又叫狄克斯特拉演算法。是從一個頂點到其餘各頂點的最短路徑演算法，解決的是有向圖中最短路徑問題。

其基本原理是：每次新擴充套件一個距離最短的點，更新與其相鄰的點的距離。當所有邊權都為正時，由於不會存在一個距離更短的沒擴充套件過的點，所以這個點的距離永遠不會再被改變，因而保證了演算法的正確性。不過根據這個原理，用Dijkstra求最短路的圖不能有負權邊，因為擴充套件到負權邊的時候會產生更短的距離，有可能就破壞了已經更新的點距離不會改變的性質。

舉例來說，如果圖中的頂點表示城市，而邊上的權重表示著城市間開車行經的距離。

一個最簡單的思路，是找出所有可能的從A到B的路徑，再通過比較，來尋找最短路徑。然而，這並沒有將問題簡化多少。因為搜尋從A到B的路徑，這本身就是很複雜的事情。而我們在搜尋所有路徑的過程中，有許多路徑已經繞了很遠，完全沒有搜尋的必要。比如從上海到紐約的路線，完全沒有必要先從上海飛到南極，再從南極飛到紐約，儘管這一路徑也是一條可行的路徑。

所以，我們需要這樣一個演算法：它可以搜尋路徑，並當已知路徑包括最短路徑時，即停止搜尋。我們先以無權網路為例，看一個可行的最短路徑演算法。

無權網路

無權網路(unweighted network)是相對於加權網路的，這裡的“權”是權重。每條邊的耗費相同，都為1。路徑的總耗費即為路徑上邊的總數。

我們用“甩鞭子”的方式，來尋找最短路徑。鞭子的長度代表路徑的距離。

手拿一個特定長度的鞭子，站在A點。甩出鞭子，能打到一些點。比如C和D。

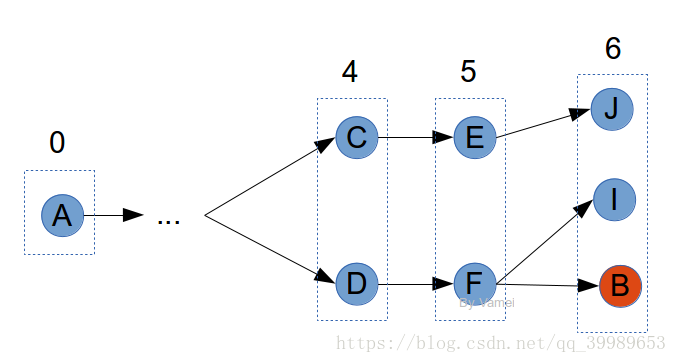
將鞭子的長度增加1。再甩出鞭子。此時，從C或D出發，尋找距離為1的鄰接點，即E和F。這些點到A點的距離，為此時鞭子的長度。

記錄點E和F，並記錄它們的上游節點。比如E(C)， F(D)。我們同樣可以記錄此時該點到A的距離，比如5。

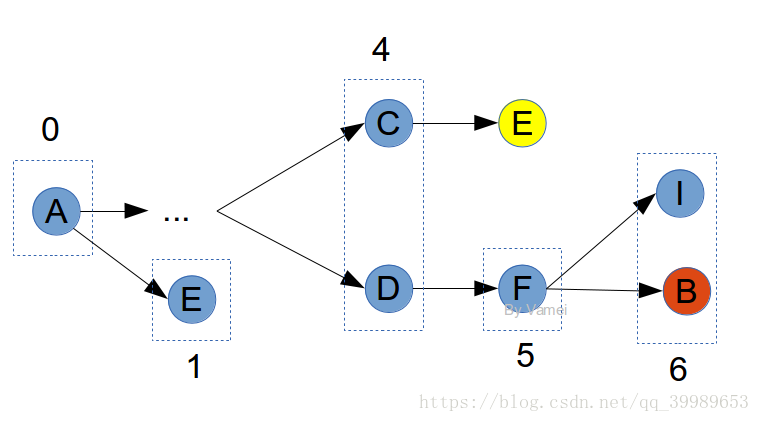
如果要記錄節點E時，發現它已經出現在之前的記錄中，這說明曾經有更短的距離到E。此時，不將E放入記錄中。畢竟，我們感興趣的是最短路徑。如下圖中的E：

黃色的E不被記錄

最初的鞭子長度為0，站在A點，只能打到A點自身。當我們不斷增加鞭子長度，第一次可以打到B時，那麼此時鞭子的長度，就是從A到B的最短距離。循著我們的記錄，倒推上游的節點，就可以找出整個最短路徑。我們的記錄本是個很有意思的東西。某個點放入記錄時，此時的距離，都是A點到該點的最短路徑。根據記錄，我們可以反推出記錄中任何一點的最短路徑。這就好像真誠對待每個人。這能保證，當你遇到真愛時，你已經是在真誠相待了。實際上，記錄將所有節點分割成兩個世界：記錄內的，已知最短距離的；記錄外的，未知的。

加權網路

在加權網路中(weighted network)，每條邊有各自的權重。當我們選擇某個路徑時，總耗費為路徑上所有邊的權重之和。

加權網路在生活中很常見，比如從北京到上海，可以坐火車，也可以坐飛機。但兩種選擇耗費的時間並不同。再比如，我們打出租車和坐公交車，都可以到市區，但車資也有所不同。在計算機網路中，由於硬體效能不同，連線的傳輸速度也有所差異。加權網路正適用於以上場景。無權網路是加權網路的一個特例。

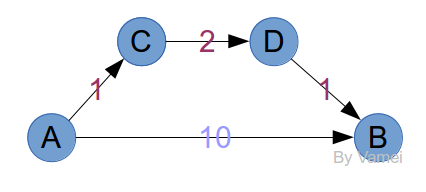
很明顯，最短路徑是A->C->D->B，因為它的總耗費只有4。按照上面的方法，我們先將A放入記錄。從A出發，有B和C兩個如果將B和C同時放入記錄，那麼記錄中的B並不符合最短距離的要求。

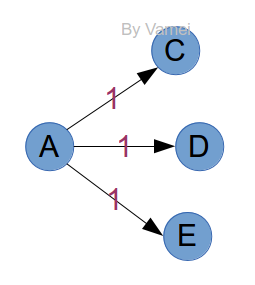
那麼，為什麼無權網路可行呢？假設某次記錄時，鞭子長度為5，那麼這次記錄點的鄰接點，必然是距離為6的點。如果這些鄰接點沒有出現過，那麼6就是它們的最短距離。所有第一次出現的鄰接點，都將加入到下次的記錄中。比如下面的例子，C/D/E是到達A的鄰接點，它們到A的最短距離必然都是1。

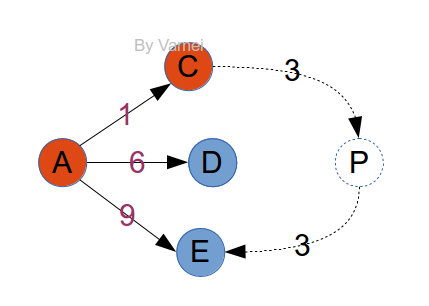
對於加權網路來說，即使知道了鄰接點，也無法判斷它們是否符合最短距離。在記錄C/D/E時，我們無法判斷未來是否存在如下圖虛線的連線，導致A的鄰接點E並不是下一步的最短距離點：

但情況並沒有我們想的那麼糟糕。仔細觀察，我們發現，雖然無法一次判定所有的鄰接點為下一步的最短距離點，但我們可以確定點C已經處在從A出發的最短距離狀態。A到C的其它可能性，比如途徑D和E，必然導致更大的成本。

也就是說，鄰接點中，有一個達到了最短距離點，即鄰接點中，到達A距離最短的點，比如上面的C。我們可以安全的把C改為已知點。A和C都是已知點，點P成為新的鄰接點。P到A得距離為4。

出於上面的觀察，我們可以將節點分為三種：

· 已知點：已知到達A最短距離的點。“我是成功人士。”

· 鄰接點：有從記錄點出發的邊，直接相鄰的點。“和成功人士接觸，也有成功的機會哦。”

· 未知點：“還早得很。” 

最初的已知點只有A。已知點的直接下游節點為鄰接點。對於鄰接點，我們需要獨立的記錄它們。我們要記錄的有：

· 當前情況下，從A點出發到達該鄰接點的最短距離。比如對於上面的點D，為6。

· 此最短距離下的上游節點。對於上面的點D來說，為A。

每次，我們將鄰接點中最短距離最小的點X轉為已知點，並將該點的直接下游節點，改為鄰接點。我們需要計算從A出發，經由X，到達這些新增鄰接點的距離：新距離 = X最短距離 + QX邊的權重。此時有兩種情況，

· 如果下游節點Q還不是鄰接點，那麼直接加入，Q最短距離 = 新距離，Q上游節點為X。

· 如果下游節點Q已經是鄰接點，記錄在冊的上游節點為Y，最短距離為y。如果新距離小於y，那麼最小距離改為新距離，上游節點也改為X。否則保持原記錄不變。

我們還用上面的圖，探索A到E的路徑：

第一步

第二步

第二步

第三步

最後，E成為已知。倒退，可以知道路徑為E, P, C, A。正過來，就是從A到E的最短路徑了。

上面的演算法是經典的Dijkstra演算法。本質上，每個鄰接點記錄的，是基於已知點的情況下，最好的選擇，也就是所謂的“貪婪演算法”(greedy algorithm)。當我們貪婪時，我們的決定是臨時的，並沒有做出最終的決定。轉換某個點成為已知點後，我們增加了新的可能性，貪婪再次起作用。根據對比。隨後，某個鄰接點成為新的“貪無可貪”的點，即經由其它任意鄰接點，到達該點都只會造成更高的成本； 經由未知點到達該點更不可能，因為未知點還沒有開放，必然需要經過現有的鄰接點到達，只會更加繞遠。好吧，該點再也沒有貪婪的動力，就被扔到“成功人士”裡，成為已知點。成功學不斷傳染，最後感染到目標節點B，我們就找到了B的最短路徑。

總結： 這個演算法只能計算單元最短路，而且不能計算負權值，這個演算法是貪心的思想， dis陣列用來儲存起始點到其他點的最短路，但開始時卻是存的起始點到其他點的初始路程。通過n-1遍的遍歷找最短。每次在剩餘節點中找dist陣列中的值最小的，加入到s陣列中，並且把剩餘節點的dist陣列更新。

程式待續。。。。。。