知識圖譜入門 (七) 知識推理
本節對本體任務推理做一個簡單的介紹,並介紹本體推理任務的分類。而後對本體推理的方法和工具做一個介紹。
知識推理簡介
知識推理任務分類
所謂推理就是通過各種方法獲取新的知識或者結論,這些知識和結論滿足語義。其具體任務可分為可滿足性(satisfiability)、分類(classification)、例項化(materialization)。
可滿足性可體現在本體上或概念上,在本體上即本體可滿足性是檢查一個本體是否可滿足,即檢查該本體是否有模型。如果本體不滿足,說明存在不一致。概念可滿足性即檢查某一概念的可滿足性,即檢查是否具有模型,使得針對該概念的解釋不是空集。
上圖是兩個不可滿足的例子,第一個本體那個是說,Man 和 Woman 的交集是空集,那麼就不存在同一個本體Allen 既是Man 又是Women。 第二個概念是說概念Eternity是一個空集,那麼他不具有模型,即不可滿足。
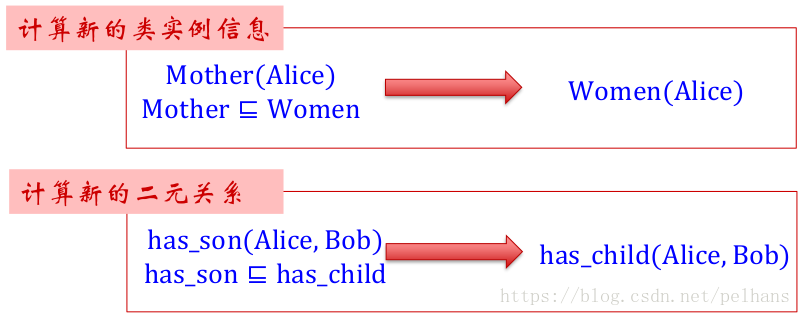
分類,針對Tbox的推理,計算新的概念包含關係。如:
即若Mother 是 Women的子集,Women是 Person的子集,那麼我們就可以得出 Mother是 Person的子集這個新類別關係。
例項化即計算屬於某個概念或關係的所有例項的集合。如:
第一個是計算新的類例項資訊,首先已知Alice 是Mother,Mother 是 Women的子集,那麼可知Alice 是一個Women。即為Women增加了一個新的例項。下面那個是計算新的二元關係,已知Alice 和Bob 有兒子,同時has_son 是has_child的子類,那麼可知Alice 和Bob has_child。
知識推理簡介
OWL本體語言是知識圖譜中最規範(W3C制定)、最嚴謹(採用描述邏輯)。表達能力最強的語言(是一階謂詞邏輯的子集),它基於RDF語法,使表示出來的文件具有語義理解的結構基礎。促進了統一詞彙表的使用,定義了豐富的語義詞彙。同時允許邏輯推理。
關於OWL語言的規範性我們再之前討論過,此處我們介紹一下它的邏輯基礎:描述邏輯。
描述邏輯
描述邏輯(Description Logic)是基於物件的知識表示的形式化,也叫概念表示語言或術語邏輯,是一階謂詞邏輯的一個可判定子集。
一個描述邏輯系統由四個基本部分組成:
- 最基本的元素:概念、關係、個體
- TBox術語集:概念術語的公理集合
- Abox斷言集:個體的斷言集合
- TBox 和 ABox上的推理機制
不同的描述邏輯系統的表示能力與推理機制由於對這四個組分的不同選擇而不同。下面對四個組分中的概念做一個簡單介紹。
最基本的元素有概念、關係、個體。
- 概念即解釋為一個領域的子集,如
- 關係解釋為該領域上的二元關係(笛卡爾積),如
- 個體解釋為一個領域內的例項,如小明:{Ming}
TBox為術語集,它是泛化的知識,是描述概念和關係的知識,被稱之為公理(Axiom)。由於概念之間存在包含關係,TBox 知識形成類似格(Lattice)的結構,這種結構是由包含關係決定的,與具體實現無關。TBox語言有定義和包含,其中定義為引入概念及關係的名稱,如Mother、Person、has_child,包含指宣告包含關係的公理,例如
ABox是斷言集,指具體個體的資訊,ABox包含外延知識(又稱為斷言(Assertion)), 描述論域中的特定個體。**描述邏輯的知識庫 , T即TBOx, A即ABOx。**ABox 語言包含概念斷言和關係斷言,概念斷言即表示一個物件是否屬於某個概念,例如Mother(Alice)、Person(Bob)。關係斷言表示兩個物件是否滿足特定的關係,例如 has_child(Alice, Bob)。
描述邏輯語義:解釋I是知識庫K的模型,當且僅當I是K中每個斷言的模型。若一個知識庫K有一個模型,則稱K是可滿足的。若斷言σ對於K的每個模型都是滿足的,則稱K邏輯蘊含σ,記為。對概念C,若K有一個模型I使得則稱C是可滿足的。
描述邏輯依據提供的構造運算元,在簡單的概念和關係上構造出複雜的概念和關係。描述邏輯至少包含以下構造運算元:交 (),並(),非 (¬),存在量詞 ()和全稱量詞 ()。有了語義之後,我們可以進行推理。通過語義來保證推理的正確和完備性。
下圖給出描述邏輯的語義表:
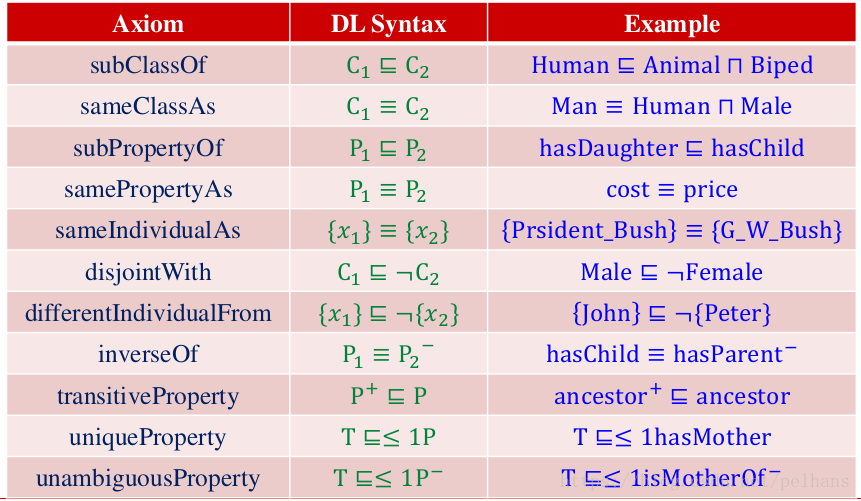
因為OWL採用描述邏輯,因此下圖給出了描述邏輯與OWL詞彙的對應表:
本體推理方法與工具介紹
基於本體推理的方法常見的有基於Tableaux運算的方法、基於邏輯程式設計改寫的方法、基於一階查詢重寫的方法、基於產生式規則的方法等。
- 基於Tableaux運算適用於檢查某一本體的可滿足性,以及例項檢測。
- 基於邏輯程式設計改寫的方法可以根據特定的場景定製規則,以實現使用者自定義的推理過程。
- 基於一節查詢重寫的方法可以高效低結合不同資料格式的資料來源,重寫方法關聯起了不同的查詢語言。以Datalog語言為中間語言,首先重寫SPARQL語言為Datalog,再將Datalog重寫為SQL查詢;
- 一種前向推理系統,可以按照一定機制執行規則從而達到某些目標,與一階邏輯類似,也有區別;
下面對上面的幾種方法做詳細介紹。
基於Tableaux運算
基於Tableaux運算適用於檢查某一本體的可滿足性,以及例項檢測。其基本思想是通過一系列規則構建Abox,以檢測可滿足性,或者檢測某一例項是否存在於某概念。這種思想類似於一階邏輯的歸結反駁。
Tableaux運算規則(以主要DL運算元舉例)如下:
這裡對第一個解釋一下,其他的類似。第一個是說如果C 和D(x) 的合取是,同時呢C(x) 和 D(x) 卻不在裡,那麼也就是說有可能只包含了部分C,而C(x)不在裡面,那麼我們就把它們新增到裡。下面我們舉個實際的例子:
現在給定如下本體,檢測例項Allen 是否在 Woman中? 即:
檢測 Woman(Allen)?其解決流程為:
- 首先加入帶反駁的結論:
初始Abox,記為 ,其內包含。
運用 規則,得到 。將其加入到中,現在的 為 。
運用 規則到 與上,得到