前言

最近在牛客網上做了幾套公司的真題，發現有關動態規劃（Dynamic Programming）演算法的題目很多。相對於我來說，演算法裡面遇到的問題裡面感覺最難的也就是動態規劃（Dynamic Programming）演算法了，於是花了好長時間，查找了相關的文獻和資料準備徹底的理解動態規劃（Dynamic Programming）演算法。一是幫助自己總結知識點，二是也能夠幫助他人更好的理解這個演算法。後面的參考文獻只是我看到的文獻的一部分。

動態規劃演算法的核心

理解一個演算法就要理解一個演算法的核心，動態規劃演算法的核心是下面的一張圖片和一個小故事。

A * "1+1+1+1+1+1+1+1 =？"
 
 *

A : "上面等式的值是多少"
B : *計算* "8!"

A *在上面等式的左邊寫上 "1+" *
A : "此時等式的值為多少"
B : *quickly* "9!"
A : "你怎麼這麼快就知道答案了"
A : "只要在8的基礎上加1就行了"
A : "所以你不用重新計算因為你記住了第一個等式的值為8!動態規劃演算法也可以說是 '記住求過的解來節省時間'"

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

由上面的圖片和小故事可以知道動態規劃演算法的核心就是記住已經解決過的子問題的解。

動態規劃演算法的兩種形式

上面已經知道動態規劃演算法的核心是記住已經求過的解，記住求解的方式有兩種：①自頂向下的備忘錄法

Fibonacci (n) = 1;   n = 0

Fibonacci (n) = 1;   n = 1

Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)

• 1
• 2
• 3
• 4
• 5

以前學c語言的時候寫過這個演算法使用遞迴十分的簡單。先使用遞迴版本來實現這個演算法：

public int fib(int n)
{
    if(n<=0)
        return 0;
    if(n==1)
        return
 
 1;
    return fib( n-1)+fib(n-2);
}
//輸入6
//輸出：8

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

先來分析一下遞迴演算法的執行流程，假如輸入6，那麼執行的遞迴樹如下：

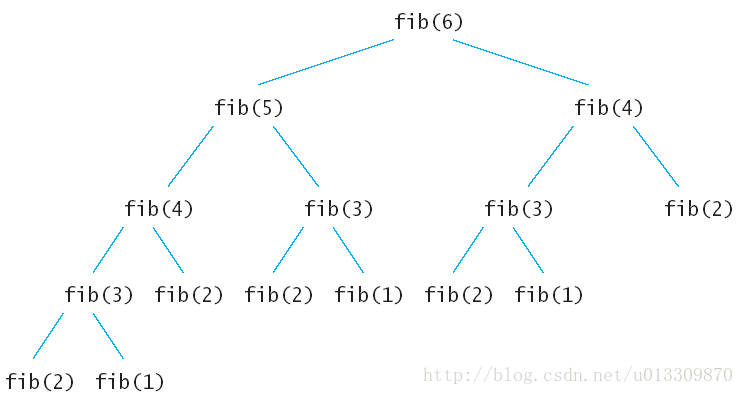
上面的遞迴樹中的每一個子節點都會執行一次，很多重複的節點被執行，fib(2)被重複執行了5次。由於呼叫每一個函式的時候都要保留上下文，所以空間上開銷也不小。這麼多的子節點被重複執行，如果在執行的時候把執行過的子節點儲存起來，後面要用到的時候直接查表呼叫的話可以節約大量的時間。下面就看看動態規劃的兩種方法怎樣來解決斐波拉契數列Fibonacci 數列問題。

①自頂向下的備忘錄法

public static int Fibonacci(int n)
{
        if(n<=0)
            return n;
        int []Memo=new int[n+1];        
        for(int i=0;i<=n;i++)
            Memo[i]=-1;
        return fib(n, Memo);
    }
    public static int fib(int n,int []Memo)
    {

        if(Memo[n]!=-1)
            return Memo[n];
    //如果已經求出了fib（n）的值直接返回，否則將求出的值儲存在Memo備忘錄中。               
        if(n<=2)
            Memo[n]=1;

        else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);  

        return Memo[n];
    }

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22

備忘錄法也是比較好理解的，建立了一個n+1大小的陣列來儲存求出的斐波拉契數列中的每一個值，在遞迴的時候如果發現前面fib（n）的值計算出來了就不再計算，如果未計算出來，則計算出來後儲存在Memo陣列中，下次在呼叫fib（n）的時候就不會重新遞迴了。比如上面的遞迴樹中在計算fib（6）的時候先計算fib（5），呼叫fib（5）算出了fib（4）後，fib（6）再呼叫fib（4）就不會在遞迴fib（4）的子樹了，因為fib（4）的值已經儲存在Memo[4]中。

②自底向上的動態規劃

備忘錄法還是利用了遞迴，上面演算法不管怎樣，計算fib（6）的時候最後還是要計算出fib（1），fib（2），fib（3）……,那麼何不先計算出fib（1），fib（2），fib（3）……,呢？這也就是動態規劃的核心，先計運算元問題，再由子問題計算父問題。

public static int fib(int n)
{
        if(n<=0)
            return n;
        int []Memo=new int[n+1];
        Memo[0]=0;
        Memo[1]=1;
        for(int i=2;i<=n;i++)
        {
            Memo[i]=Memo[i-1]+Memo[i-2];
        }       
        return Memo[n];
}

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13

自底向上方法也是利用陣列儲存了先計算的值，為後面的呼叫服務。觀察參與迴圈的只有 i，i-1 , i-2三項，因此該方法的空間可以進一步的壓縮如下。

public static int fib(int n)
    {
        if(n<=1)
            return n;

        int Memo_i_2=0;
        int Memo_i_1=1;
        int Memo_i=1;
        for(int i=2;i<=n;i++)
        {
            Memo_i=Memo_i_2+Memo_i_1;
            Memo_i_2=Memo_i_1;
            Memo_i_1=Memo_i;
        }       
        return Memo_i;
    }

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16

一般來說由於備忘錄方式的動態規劃方法使用了遞迴，遞迴的時候會產生額外的開銷，使用自底向上的動態規劃方法要比備忘錄方法好。
你以為看懂了上面的例子就懂得了動態規劃嗎？那就too young too simple了。動態規劃遠遠不止如此簡單，下面先給出一個例子看看能否獨立完成。然後再對動態規劃的其他特性進行分析。

動態規劃小試牛刀

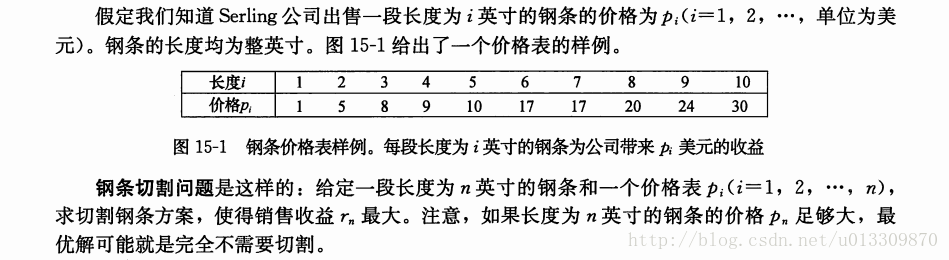
例題：鋼條切割

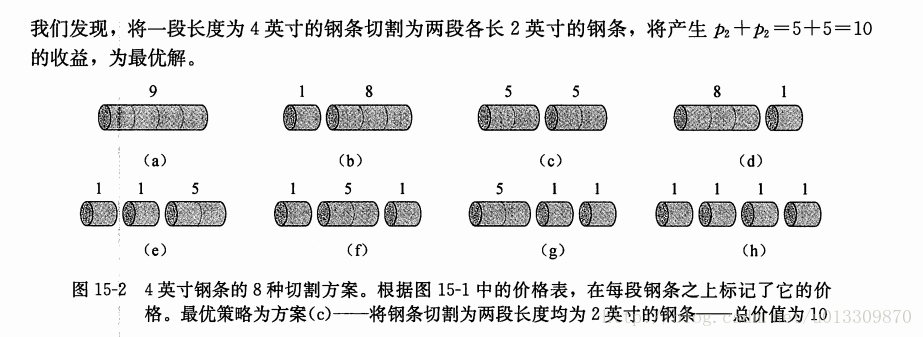
上面的例題來自於演算法導論
關於題目的講解就直接截圖演算法導論書上了這裡就不展開講。現在使用一下前面講到三種方法來來實現一下。
①遞迴版本

public static int cut(int []p,int n)
    {
        if(n==0)
            return 0;
        int q=Integer.MIN_VALUE;
        for(int i=1;i<=n;i++)
        {
            q=Math.max(q, p[i-1]+cut(p, n-i));  
        }
        return q;
    }

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11

遞迴很好理解，如果不懂可以看上面的講解，遞迴的思路其實和回溯法是一樣的，遍歷所有解空間但這裡和上面斐波拉契數列的不同之處在於，在每一層上都進行了一次最優解的選擇，q=Math.max(q, p[i-1]+cut(p, n-i));這個段語句就是最優解選擇，這裡上一層的最優解與下一層的最優解相關。

②備忘錄版本

public static int cutMemo(int []p)
    {
        int []r=new int[p.length+1];
        for(int i=0;i<=p.length;i++)
            r[i]=-1;                        
        return cut(p, p.length, r);
    }
    public static int cut(int []p,int n,int []r)
    {
        int q=-1;
        if(r[n]>=0)
            return r[n];
        if(n==0)
            q=0;
        else {
            for(int i=1;i<=n;i++)
                q=Math.max(q, cut(p, n-i,r)+p[i-1]);
        }
        r[n]=q;

        return q;
    }

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13
• 14
• 15
• 16
• 17
• 18
• 19
• 20
• 21
• 22

有了上面求斐波拉契數列的基礎，理解備忘錄方法也就不難了。備忘錄方法無非是在遞迴的時候記錄下已經呼叫過的子函式的值。這道鋼條切割問題的經典之處在於自底向上的動態規劃問題的處理，理解了這個也就理解了動態規劃的精髓。

③自底向上的動態規劃

public static int buttom_up_cut(int []p)
    {
        int []r=new int[p.length+1];
        for(int i=1;i<=p.length;i++)
        {
            int q=-1;
            //①
            for(int j=1;j<=i;j++)
                q=Math.max(q, p[j-1]+r[i-j]);
            r[i]=q;
        }
        return r[p.length];
    }

• 1
• 2
• 3
• 4
• 5
• 6
• 7
• 8
• 9
• 10
• 11
• 12
• 13

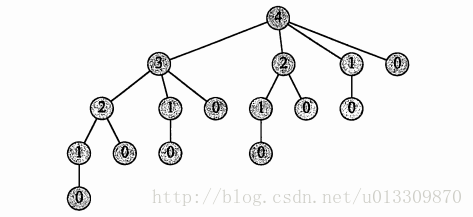
自底向上的動態規劃問題中最重要的是理解註釋①處的迴圈，這裡外面的迴圈是求r[1],r[2]……，裡面的迴圈是求出r[1],r[2]……的最優解，也就是說r[i]中儲存的是鋼條長度為i時劃分的最優解，這裡面涉及到了最優子結構問題，也就是一個問題取最優解的時候，它的子問題也一定要取得最優解。下面是長度為4的鋼條劃分的結構圖。我就偷懶截了個圖。

動態規劃原理

雖然已經用動態規劃方法解決了上面兩個問題，但是大家可能還跟我一樣並不知道什麼時候要用到動態規劃。總結一下上面的斐波拉契數列和鋼條切割問題，發現兩個問題都涉及到了重疊子問題，和最優子結構。

①最優子結構

用動態規劃求解最優化問題的第一步就是刻畫最優解的結構，如果一個問題的解結構包含其子問題的最優解，就稱此問題具有最優子結構性質。因此，某個問題是否適合應用動態規劃演算法，它是否具有最優子結構性質是一個很好的線索。使用動態規劃演算法時，用子問題的最優解來構造原問題的最優解。因此必須考查最優解中用到的所有子問題。

②重疊子問題

在斐波拉契數列和鋼條切割結構圖中，可以看到大量的重疊子問題，比如說在求fib（6）的時候，fib（2）被呼叫了5次，在求cut（4）的時候cut（0）被呼叫了4次。如果使用遞迴演算法的時候會反覆的求解相同的子問題，不停的呼叫函式，而不是生成新的子問題。如果遞迴演算法反覆求解相同的子問題，就稱為具有重疊子問題（overlapping subproblems）性質。在動態規劃演算法中使用陣列來儲存子問題的解，這樣子問題多次求解的時候可以直接查表不用呼叫函式遞迴。

動態規劃的經典模型

線性模型

線性模型的是動態規劃中最常用的模型，上文講到的鋼條切割問題就是經典的線性模型，這裡的線性指的是狀態的排布是呈線性的。【例題1】是一個經典的面試題，我們將它作為線性模型的敲門磚。

【例題1】在一個夜黑風高的晚上，有n（n <= 50）個小朋友在橋的這邊，現在他們需要過橋，但是由於橋很窄，每次只允許不大於兩人通過，他們只有一個手電筒，所以每次過橋的兩個人需要把手電筒帶回來，i號小朋友過橋的時間為T[i]，兩個人過橋的總時間為二者中時間長者。問所有小朋友過橋的總時間最短是多少。

每次過橋的時候最多兩個人，如果橋這邊還有人，那麼還得回來一個人（送手電筒），也就是說N個人過橋的次數為2*N-3（倒推，當橋這邊只剩兩個人時只需要一次，三個人的情況為來回一次後加上兩個人的情況…）。有一個人需要來回跑，將手電筒送回來（也許不是同一個人，realy？！）這個回來的時間是沒辦法省去的，並且回來的次數也是確定的，為N-2，如果是我，我會選擇讓跑的最快的人來幹這件事情，但是我錯了…如果總是跑得最快的人跑回來的話，那麼他在每次別人過橋的時候一定得跟過去，於是就變成就是很簡單的問題了，花費的總時間：

T = minPTime * (N-2) + (totalSum-minPTime)

來看一組資料 四個人過橋花費的時間分別為 1 2 5 10，按照上面的公式答案是19，但是實際答案應該是17。

具體步驟是這樣的：

第一步：1和2過去，花費時間2，然後1回來（花費時間1）；

第二歩：3和4過去，花費時間10，然後2回來（花費時間2）；

第三部：1和2過去，花費時間2，總耗時17。

所以之前的貪心想法是不對的。我們先將所有人按花費時間遞增進行排序，假設前i個人過河花費的最少時間為opt[i]，那麼考慮前i-1個人過河的情況，即河這邊還有1個人，河那邊有i-1個人，並且這時候手電筒肯定在對岸，所以opt[i] = opt[i-1] + a[1] + a[i] (讓花費時間最少的人把手電筒送過來，然後和第i個人一起過河)如果河這邊還有兩個人，一個是第i號，另外一個無所謂，河那邊有i-2個人，並且手電筒肯定在對岸，所以opt[i] = opt[i-2] + a[1] + a[i] + 2*a[2] (讓花費時間最少的人把電筒送過來，然後第i個人和另外一個人一起過河，由於花費時間最少的人在這邊，所以下一次送手電筒過來的一定是花費次少的，送過來後花費最少的和花費次少的一起過河，解決問題)
所以 opt[i] = min{opt[i-1] + a[1] + a[i] , opt[i-2] + a[1] + a[i] + 2*a[2] }

區間模型

區間模型的狀態表示一般為d[i][j]，表示區間[i, j]上的最優解，然後通過狀態轉移計算出[i+1, j]或者[i, j+1]上的最優解，逐步擴大區間的範圍，最終求得[1, len]的最優解。

【例題2】給定一個長度為n（n <= 1000）的字串A，求插入最少多少個字元使得它變成一個迴文串。
典型的區間模型，迴文串擁有很明顯的子結構特徵，即當字串X是一個迴文串時，在X兩邊各新增一個字元’a’後，aXa仍然是一個迴文串，我們用d[i][j]來表示A[i…j]這個子串變成迴文串所需要新增的最少的字元數，那麼對於A[i] == A[j]的情況，很明顯有 d[i][j] = d[i+1][j-1] （這裡需要明確一點，當i+1 > j-1時也是有意義的，它代表的是空串，空串也是一個迴文串，所以這種情況下d[i+1][j-1] = 0）；當A[i] != A[j]時，我們將它變成更小的子問題求解，我們有兩種決策：

1、在A[j]後面新增一個字元A[i]；

2、在A[i]前面新增一個字元A[j]；

根據兩種決策列出狀態轉移方程為：

d[i][j] = min{ d[i+1][j], d[i][j-1] } + 1; (每次狀態轉移，區間長度增加1)

空間複雜度O(n^2)，時間複雜度O(n^2)， 下文會提到將空間複雜度降為O(n)的優化演算法。

揹包模型

揹包問題是動態規劃中一個最典型的問題之一。由於網上有非常詳盡的揹包講解，這裡只將常用部分抽出來。

【例題3】有N種物品（每種物品1件）和一個容量為V的揹包。放入第 i 種物品耗費的空間是Ci，得到的價值是Wi。求解將哪些物品裝入揹包可使價值總和最大。f[i][v]表示前i種物品恰好放入一個容量為v的揹包可以獲得的最大價值。決策為第i個物品在前i-1個物品放置完畢後，是選擇放還是不放，狀態轉移方程為：

f[i][v] = max{ f[i-1][v], f[i-1][v – Ci] +Wi }

時間複雜度O(VN)，空間複雜度O(VN) （空間複雜度可利用滾動陣列進行優化達到O(V) ）。

動態規劃題集整理

2、最大M子段和
Max Sum ★☆☆☆☆
最長公共子串 ★★☆☆☆

3、線性模型
Skiing ★☆☆☆☆

總結

弄懂動態規劃問題的基本原理和動態規劃問題的幾個常見的模型，對於解決大部分的問題已經足夠了。希望能對大家有所幫助，轉載請標明出處http://write.blog.csdn.net/mdeditor#!postId=75193592，創作實在不容易，這篇部落格花了我將近一個星期的時間。

參考文獻

1.演算法導論