bzoj1367 可並堆
題面
參考:《左偏樹的特點及運用——黃河源》
我們將這個數列劃為很多個互不相交的區間,每一段區間內的 \(b\) 是相等的,即
- \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=w[i]?\), \(l[i],r[i]?\) 為區間 \(i?\) 的左右端點
先假設題目時要求b不下降的(比較好討論),那麽答案應該會呈現出這樣子:
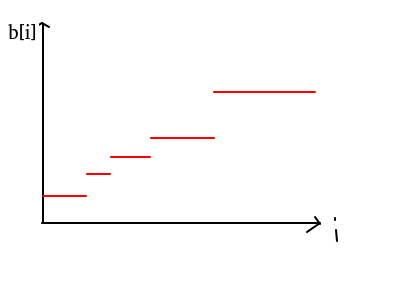
定理一:對於單個區間的最優解為其中位數,即 \(a[l[i]],a[l[i]+1],...,a[r[i]]\) 的最優解為 \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=\) 中位數。
- 由絕對值的幾何意義可得.
如果我們將"b不下降"這一條件忽略
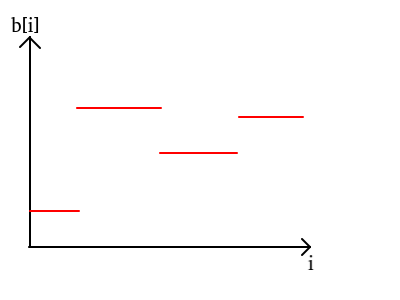
在討論如何將不合法的最優解轉化為合法的最優解之前,先來了解一些結論:
結論一:對於一段連續的a不下降(可能由多個區間組成),則 \(b[i]=a[i]\) 時為最優解。
證明:該段絕對值之差為0.
引理一:對於相鄰的兩個區間 \([l[i]],\ r[i]]\ and\ [l[i+1],\ r[i+1]]?\) , \(u,v?\) 為其最優解,若 \(u\le v?\), 則 \([l[i],r[i+1]]?\) 的區間最優解為 \(b[l[i]]=b[l[i]+1]=...=b[r[i]]=u,\ b[l[i+1]]=b[l[i+1]+1]=...=b[r[i+1]]=v?\)
證明:子問題最優 -> 整體最優.
引理二:對於相鄰的兩個區間 \([l[i]],\ r[i]]\ and\ [l[i+1],\ r[i+1]]\) , \(u,v\) 為其最優解,若 \(v < u\) ,則 \(b[r[i]]\le u, v\le b[l[i+1]].\)
畫個圖:
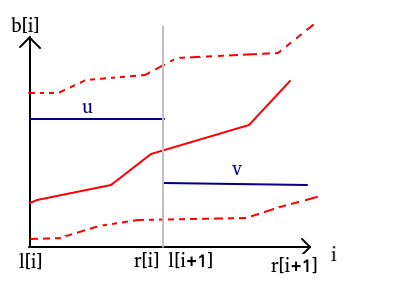
因為除此之外的情況(虛線)一定不會比這種情況更好
如:上面那條虛線沒有u+右邊部分更優,下面那條虛線沒有v+左邊部分更優
而u+右邊部分與v+左邊部分是屬於紅色折線的.
結論二:對於任意一個序列 \(a[1] , a[2] , ... , a[n]\) ,如果最優解為 \(( u , u , ... , u )\)
給出 \(u\le u‘\le b[1]\) 的證明,後者類似可證.
證明:
對於 \(n=1,a[1]=u,?\) 顯然成立.
假設對於n是成立的,那麽將 \(b[1],b[2]...b[n],b[n+1]\) 都設為 \(b[1]\) , 若解變得更壞了,則最優解應該是 \((u,u,...,u,b[n+1])\) 而不是 \((u,u,...u,u)\), 而由幾何意義得 \((b[1],b[1]...b[1])\) 比 \((u‘,u‘,...,u‘)\) 會差,故對於 \(n+1\) 也成立.
由數學歸納原理可得命題成立.
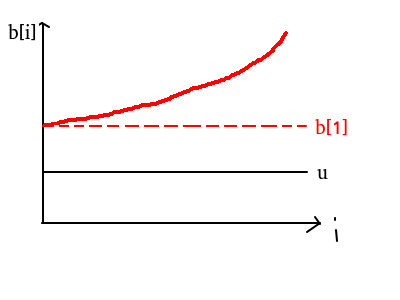
至此,我們已經可以將局部最優解合成整體最優解了!
一:
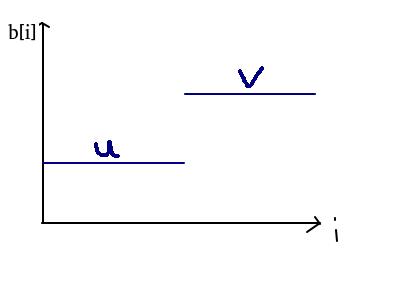
u,v為兩段區間的最優解,由引理一全局最優解為 \((u,u,...,u,v,v,...,v)\).
二:
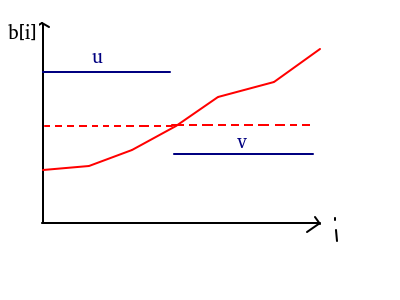
這種情況較為復雜,由引理二可得最優解一定是左邊\(\le u\), 右邊的 \(\geq v\),即為紅色部分,
又由結論二得虛線部分比紅色部分更優(其實是不會更差), 所以這個整個區間的最優解一定為一個定值!
註:其實左邊的虛線是比右邊低的,但是左邊的虛線越往上越優,右邊的虛線越往下越優,故最優時它們高度相同,為一定值。
接下來就轉換成求這個定值了。
由定理一,值該定值即為整個數列的中位數!!
所以一開始假設每個數就是一個區間,然後不斷合並區間,最終知道全局最優解。
- 假設我們已經找到前 \(k\) 個數 \(a[1], a[2], ... , a[k] (k<n)\) 的最優解,
- 得到 \(m\) 個區間組成的隊列, 對應的解為 \((w[1], w[2] , ... , w[m])\),
- 現在要加入 \(a[k+1]\), 並求出前 \(k+1\) 個數的最優解。
- 首先我們把 \(a[k+1]\) 作為一個新區間直接加入隊尾,令 \(w[m+1]=a[k+1]\) ,
- 然後不斷檢查隊尾兩個區間的解 \(w[m]\) 和 \(w[m+1]\),如果 ?\(w[m] > w[m+1]\) ,
- 我們需要將最後兩個區間合並,並找出新區間的最優解(也就是序列 \(a?\) 中,下標在這個新區間內的各項的中位數)。
- 重復這個合並過程,直至 \(w[1] ≤ w[2] ≤ ... ≤ w[m]?\) 時結束,然後繼續處理下一個數。
- 畫圖理解...
現在我們需要考慮一下數據結構的選取,
算法中涉及到以下兩種操作:
1.合並兩個有序集
2.查詢某個有序集內的中位數
我們很容易想到平衡樹,但是就算是啟發式合並,復雜度也有 \(O(nlog^2n)?\), \(1e6?\) 過不了.
我們可以用大根堆來維護每個區間內的中位數,我們發現右端的堆都是單個元素的加入,只要一下降,就會合並,所以合並是正確的。
“通過進一步分析,我們發現,只有當某一區間內的中位數比後一區間內的中位數大時,合並操作才會發生,也就是說,任一區間與後面的區間合並後,該區間內的中位數不會變大。於是我們可以用最大堆來維護每個區間內的中位數,當堆中的元素大於該區間內元素的一半時,刪除堆頂元素,這樣堆中的元素始終為區間內較小的一半元素,堆頂元素即為該區間內的中位數。” —— 黃源河
堆頂元素即為該區間內的中位數。
考慮到我們必須高效地完成合並操作,左偏樹是一個理想的選擇,每個操作都是 \(O(logn)\),
總時間復雜度 \(O(nlogn)?\).
bzoj1367 可並堆
