概率論面試系列第一彈: 貝葉斯公式
貝葉斯公式是一個非常常用的概率論裡的關於條件概率的公式,是資料科學麵試中的常見題型。掌握貝葉斯公式的原理並且使用該公式解決這些問題是資料科學家求職者的必備技能。
條件概率(conditional probability)的定義
條件概率Pr[A|B]必須定義在兩個事件A和B上,含義是在B發生的條件下,A發生的概率。
可以想象B是已經滿足的條件,條件概率即是在給定條件下A事件的概率。除非A與B獨立,否則B的發生會影響A,因此一定有 與
不想等。
數學上,
為A與B同時發生的概率與B發生的概率的比例。
條件概率的幾何意義
幾何上,可以用文恩圖表示事件A與B:
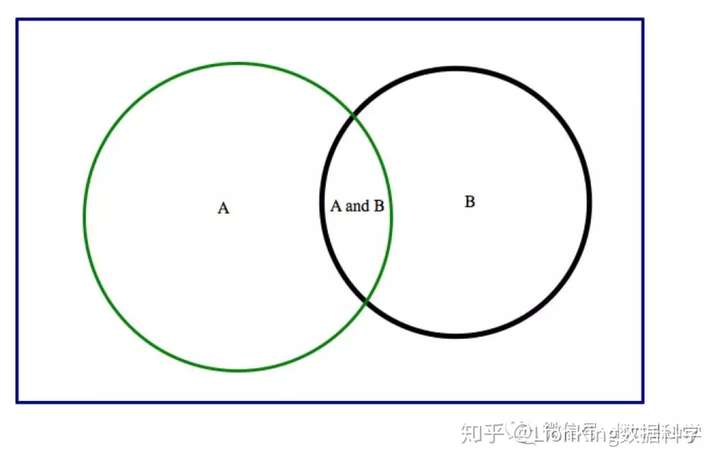
B已經滿足條件可以看作全集是B,即黑色圈出的區域,在該區域中發生A,對應A與B的交集區域。因此概率為A與B交際區域的面積與B的面積的比例。
全概率公式
全概率公式非常直觀,其含義是如果有一些互斥的事件 , 它們的並集為全集。則任何事件A發生的概率可以拆分為每一個
的概率之和。
數學上,
由條件概率的定義,等價於
全概率公式的幾何意義
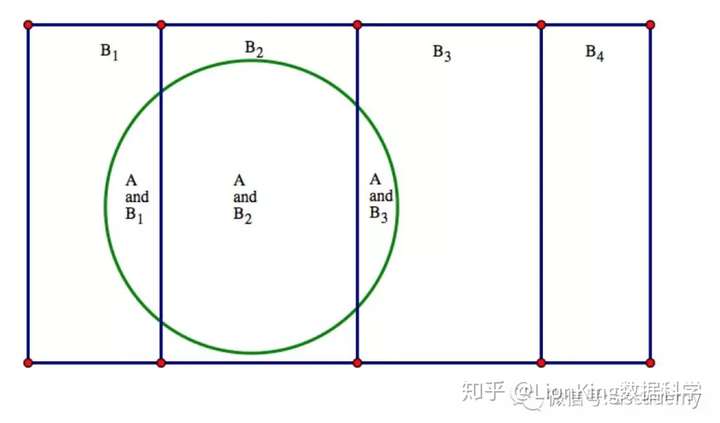
A被 這些事件劃分成了
,因此A的面積為這些面積之和。
貝葉斯公式
貝葉斯公式對於兩個事件A和B定義,只要事件B的概率非0,有如下關係:
推導非常容易:
例子
貝葉斯公式一般結合全概率公式使用,我們以一個簡單的例子說明:
Q: 某城市發生了一起汽車撞人逃跑事件,該城市只有兩種顏色的車,藍20%綠80%,事發時現場有一個目擊者,他指證是藍車,但是根據專家在現場分析,當時那種條件能看正確的可能性是80%,那麼,肇事的車是藍車的概率是多少?
A: 目擊者指證藍車記為事件B, 肇事的車是藍車記為事件A, 需要計算條件概率 。
由貝葉斯公式,只需要計算 ,以及
。
根據題目條件, 。
比較困難的是計算 本身。為了計算
,我們使用全概率公式:
其中 為A的補事件,即肇事的車是綠車。
前面兩項已經知道, ,關鍵是最後一項
,即肇事的車是綠車的條件下,目擊者指正該車為藍車的概率。
這一概率就是目擊者看錯的概率0.2。
因此,我們有
根據貝葉斯公式
練習題
我們對貝葉斯公式的介紹到這裡就告一段落,大家可以嘗試以下這些練習題,都是知名網際網路的面試真題哦。
- 有8個箱子,現在有一封信,這封信放在這8個箱子中每一個的概率均為1/10, 不放在任何一個箱子的概率為1/5, 現在我開啟1號箱子發現是空的,求下面7個箱子中含有這封信的概率?
- 一個盒子裡面有2張撲克牌有正反兩面,有1張撲克牌只有正面。隨機地取出了一張牌看到了正面,求該撲克牌的對面也是正面的概率。
- 你有三位好友,他們都在西雅圖工作,西雅圖是出了名的愛下雨,每天下雨的概率高達2/3。假設你的好友視力都不是很好並且辦公室的視野也一般,因此以1/3的概率能正確地判斷是否在下雨。假如他們中恰好有兩位告訴你今天西雅圖在下雨,問西雅圖實際上在下雨的概率是多少?
