前言

理論

在學習馬爾科夫鏈的時候，我有一篇譯文《馬爾科夫鏈和馬爾科夫鏈蒙特卡洛方法》中提到了對於馬爾科夫鏈，存在唯一的一個穩態分佈，也就是說當馬爾科夫鏈達到穩態分佈以後，其後得到的所有轉移狀態都具有相同的概率分佈。而Q-learning的最終目的就是利用價值迭代演算法尋找最優穩態(策略)。
通俗點將Q-learning的根本目的就是尋找在某種狀態下采取某種策略得到的價值是多少，比如踩雷，在某個格子，我標雷或者點開，如果炸了，就懲罰，如果沒炸就獎勵

類似於隱馬爾科夫模型(HMM)，我們也需要提前知道一些變數，以掃雷為例：

• S：狀態，當前在哪個格子上
• A：行為，對當前格子標雷還是踩下去
• r：長期獎勵和短期獎勵的折扣因子，短期獎勵就是說炸了我就扣分扣到你懷疑人生，長期獎勵就是價值函式，即根據以往經驗，我去下一個格子標雷或者踩下去是個啥情況
• P：狀態轉移矩陣，維度是[行為*狀態]，與HMM不同的是，Qlearning是依據狀態轉移和採取的行動得到下一個狀態，即當前格子選擇完處理行為後，下一個格子我會去哪裡踩
• R：短期獎勵

最終目的：

• Q：價值函式

更新價值函式的迭代流程：

• 初始化當前狀態：踩到哪個格子了
• 在當前狀態下采取哪個行動(標雷，踩下去)
• 計算每種行動獲得的反饋，計算哪個行動得到最大的價值
• 根據狀態轉移矩陣得到下一次我可能去探雷的位置，重複2和3步驟

其中最主要的是怎麼獲取行動反饋，答案就是一句長期獎勵和短期獎勵，大概意思就是以下兩項的和：

• 短期獎勵：R[當前狀態][當前行為]
• 長期獎勵：折扣因子* 依據當前狀態和行為轉移到下一個狀態後再採取的所有可能行為中依據以往經驗能得到的最大獎勵，即
  $r$
  ×max(q[下一個狀態][所有的下一個行為]) r\times max(q[下一個狀態][所有的下一個行為])
  然後根據這個最大獎勵更新Q[當前狀態][當前行為]
  $Q[當前狀態][當前行為]=(1-\alpha)Q[當前狀態][當前行為]+\alpha (R+r\times max(Q[下一個狀態][所有的行為]))$
  其實這部分為看到了好幾種更新方法：

你沒看錯，理論到此結束，最主要的就是如何依據短期利益和長期利益去確定當前狀態下采取行動所獲得的最大獎勵。

• 知乎上@牛阿的回答
  

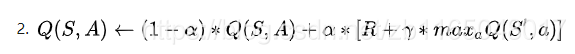
• 參考部落格1的方法
  $Q=R+r*max(Q[next\_state][action\_next])$

• 參考部落格2的方法更奇怪，這裡就不貼了額，有興趣自己去看看
  不過所有的程式碼意思幾乎都是在長遠利益中選擇最大值，但是長遠利益的計算方法有所不同，最後更新方法也有點區別，這個可能是屬於不同的更新演算法，後續繼續學習應該能知道

虛擬碼實現：

state=1;//把踩雷遊戲的最左上角的格子當做初始狀態
while !finish_game:
	action=random(0,1);//0是標記雷，1是踩下去
	next_state=P[state][action];//依據當前狀態和行為得到下一個位置
	for next_action in [0,1]//踩雷和標雷都計算
		temp_reward[next_state][next_action]=Q[next_state][next_action]
	Q[state][action]=(1-a)*Q[state][aciton]+a*[R+max(temp_reward[nextstate][:])]

貌似看著不難，後面找個啥例子再深入瞭解一波。

後記