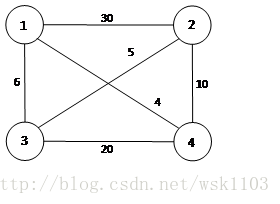
1. 某售貨員要到4個城市去推銷商品，已知各城市之間的路程，如右圖所示。請問他應該如何選定一條從城市1出發，經過每個城市一遍，最後回到城市1的路線，使得總的周遊路程最小？並分析所設計演算法的計算時間複雜度。
   
   (1) 演算法設計思路
   解向量：{1,2,3,4,1}{1,2,4,3,1,}{1,3,4,2,1}{1,3,2,4,1}{1,4,2,3,1}{1,4,3,2,1}
   解空間：是一個排序樹，樹的葉結點個數為（n-1）!=6
   上界函式：當前第一次所得到的值作為約束條件，然後比該值小時更新約束值
   int n,圖的頂點數，int[] x 當前解，int[] bestx 當前最優解，int[][] a 圖的鄰接矩陣，int cc 當前費用，int bestc 當前最優值，No 無邊標記
   (2) 演算法實現的虛擬碼及其計算時間複雜度分析
   求解旅行售貨員問題的演算法back（int t）
   輸入：t為當前城市的個數
   輸出：最短路徑和其對應值

s1:  If (t=n){
s2: if (a[x[n-1]][x[n]]!=No&&a[x[n]][1]!=No && (cc+a[x[n-1]][n]+a[x[n]][1])<bestc || bestc=No){
s3: for (inti =1 to n )best[i]=x[i]
s4: bestc=cc+ a[x[n-1]][n]+a[x[n]][1]
s5: }
s6:  else{
s7: for (inti =t to n){
s8: if(a[x[t-1]][i]!=No && (cc+a[x[n-1]][n
 
]+a[x[n]][1]<bestc || bestc =No)){
s9: swap(x[t],x[i]) ;
s10: cc+=a[x[t-1]][t];
s11: back(t+1)
s12: cc-=a[x[t-1]][t]
s13: swap(x[t],x[i])
s14: }
s15:  }

演算法fucntionA的計算時間複雜度分析：
O(n!)

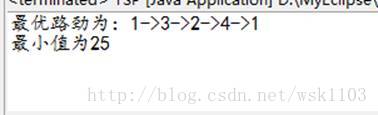
(3) 實驗程式碼及執行結果

    public class TSP {
        static int[] x = new int[5];
        static int[] bestx = new int
 
[5];
        static int[][] a = new int[5][5];
        static int cc = 0;
        static int no = 10000;
        static int bestc = no;
        static int n = 4;

        static void back(int i) {
            if (i == n) {
                if (a[x[n - 1]][x[n]] != 0
                        && a[x[n]][1] != 0
                        && (cc + a[x[n - 1]][x[n]] + a[x[n]][1] < bestc || bestc == 0)) {
                    for (int j = 1; j <= n; j++)
                        bestx[j] = x[j];
                    bestc = cc + a[x[n - 1]][x[n]] + a[x[n]][1];
                }
            } else {
                for (int j = i; j <= n; j++) {
                    // 是否可進入x[j]子樹?
                    if (a[x[i - 1]][x[j]] != 0
                            && (cc + a[x[i - 1]][x[i]] < bestc || bestc == 0)) {
                        // 搜尋子樹
                        // swap(x[i], x[j]);
                        int temp1 = x[i];
                        x[i] = x[j];
                        x[j] = temp1;
                        cc += a[x[i - 1]][x[i]]; // 當前費用累加
                        back(i + 1); // 排列向右擴充套件,排列樹向下一層擴充套件
                        cc -= a[x[i - 1]][x[i]];
                        // swap(x[i], x[j]);
                        int temp2 = x[i];
                        x[i] = x[j];
                        x[j] = temp2;
                    }
                }
            }
        }

        // private static void swap(int i, int j) {
        // // TODO Auto-generated method stub
        // int temp = i;
        // i = j;
        // j = temp;
        // }

        public static void main(String[] args) {
            a[1][1] = no;
            a[1][2] = 30;
            a[1][3] = 6;
            a[1][4] = 4;
            a[2][1] = 30;
            a[2][2] = no;
            a[2][3] = 5;
            a[2][4] = 10;
            a[3][1] = 6;
            a[3][2] = 5;
            a[3][3] = no;
            a[3][4] = 20;
            a[4][1] = 4;
            a[4][2] = 10;
            a[4][3] = 20;
            a[4][4] = no;

            for (int i = 0; i <= 4; i++)
                x[i] = i;
            // x[1]=1;
            // x[2]=3;x[3]=2;x[4]=4;
            back(2);
            System.out.print("最優路勁為：");
            for (int i = 1; i <= 4; i++)
                System.out.print(bestx[i]+"->");
            System.out.println(x[1]);
            System.out.println("最小值為"+bestc);
        }
    }

//

//

(4) 體會
用回溯演算法搜尋排列樹的演算法框架可以描述為

void back(int t){
if (t>n) output(x);
else for (inti =t,i<n;i++){
swap(x[t],x[i]);
if( contriant(t)&&bound(t)) back(t+1)
swap(x[t],x[i])
}
}

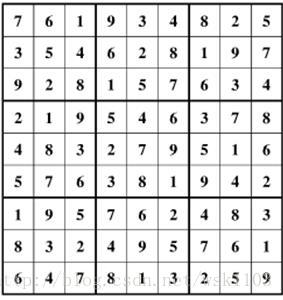
1. 數獨遊戲：九宮格是在81個格子(9×9)中，要滿足以下條件：① 每個橫行和豎列中的9個格子都包含數字1～9，且不重複；② 每個黑色粗實線圍住的9個格子(3×3)都包含數字1～9，且不重複。如圖所示：
   要求：找出給定數字的九宮格。
   輸入：輸入9行9列81個數字，其中0表示要填的數字。
   輸出：輸出滿足條件的九宮格。
   
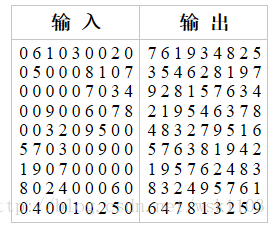
   某測試樣例如下：
   
   (1) 演算法設計思路
   數獨遊戲是N後問題的變形版本。將n*n看成二維矩陣，行i列j，解空間是完成n叉樹。
   先判斷要變化的數是否為0，如果為0，在行，列和小九宮格中判斷有沒有相同數字，有相同數字則+1，直到9，如果不為0，直接變化下一個數。

(2) 演算法實現的虛擬碼及其計算時間複雜度分析
求解數獨遊戲的演算法back(int i,int j)
輸入：陣列 的行i，列j
輸出：滿足條件的九宮格

s16:  if(i=8並且j=9){
s17: 輸出滿足條件的九宮格
s18: }
s19: if (j=9){
s20: j=0;i++
s21: } 
s22:  if (x[i][j]=0)
s23: for (int n=1 to 9){
s24: if (判斷是否在行，列，小九宮格中出現重複的值){
s25: x[i][j]=n;
s26: back(i,j+1)
s27: x[i][j]=0;
s28: }
s29: else back(i,j+1)

演算法fucntionB的計算時間複雜度分析：
O(n^n)

(3) 實驗程式碼及執行結果

    public class 數獨遊戲 {
        static int[][] bestx = new int[9][9];
        static int[][] x = { { 0, 6, 1, 0, 3, 0, 0, 2, 0 },
                { 0, 5, 0, 0, 0, 8, 1, 0, 7 }, { 0, 0, 0, 0, 0, 7, 0, 3, 4 },
                { 0, 0, 9, 0, 0, 6, 0, 7, 8 }, { 0, 0, 3, 2, 0, 9, 5, 0, 0 },
                { 5, 7, 0, 3, 0, 0, 9, 0, 0 }, { 1, 9, 0, 7, 0, 0, 0, 0, 0 },
                { 8, 0, 2, 4, 0, 0, 0, 6, 0 }, { 0, 4, 0, 0, 1, 0, 2, 5, 0 }, };;
        static int cc = 0;
        static int bestc;

        static void back(int i, int j) {
            if (i == 8 && j == 9) {
                for (int a = 0; a <= 8; a++)
                    for (int b = 0; b <=8; b++)
                        bestx[a][b] = x[a][b];
                return;
            }
            //如果j=9，則重置j，然後行+1
            if (j == 9) {
                j = 0;
                i++;
            }
            if (x[i][j] == 0)
                for (int n = 1; n < 10; n++) {
                    if (!boo(i, j, n)) {//判斷是否在行，列，小九宮格中出現重複的值
                        x[i][j] = n;
                        back(i, j + 1);
                        x[i][j] = 0;
                    }
                }
            else
                back(i, j + 1);
        }
        //判斷是否在行，列，小九宮格中出現重複的值
        static boolean boo(int i, int j, int k) {
            int m = i / 3;
            int n = j / 3;
            for (int a = 0; a < 9; a++) {
                //判斷行
                if (k == x[i][a])
                    return true;
                //判斷列
                if (k == x[a][j])
                    return true;
                //判斷小九宮格
                if (k == x[3 * m + a / 3][3 * n + a % 3])
                    return true;
            }
            return false;
        }

        public static void main(String[] args) {
            System.out.println("test");
            back(0, 0);
            System.out.println("test");
            for (int i = 0; i < 9; i++) {
                for (int j = 0; j < 9; j++) {
                    if (j < 8)
                        System.out.print(bestx[i][j] + " ");
                    else {
                        System.out.println(bestx[i][j]);
                    }
                }
            }
        }
    }

/
(4) 體會
回溯演算法一般都有一個套路，先找出問題的解空間，再思考回溯方法。
用回溯演算法搜尋子集樹的一般演算法可以描述為：

    void back(int i){
    if (i>n) output(x);
    else 
    for (int j=0 to n){
    x[t]=i,
    if (constraint(i)&&bound(i)) back(i+1)
    }
    }