轉載請註明出處： 轉載自  Thinkgamer的CSDN部落格：blog.csdn.net/gamer_gyt

1：稀疏矩陣的背景

2：什麼是稀疏矩陣？

3：為什麼要對稀疏矩陣進行壓縮儲存以及壓縮儲存的方式？

4：稀疏矩陣的相關運算

一：背景

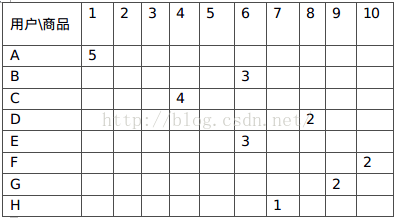
        第一此介紹稀疏矩陣是在資料結構學習時，然後當時並沒有多麼用心的去學習它，因為，感覺它在實際應用中很少遇見，直到後來自己看了基於使用者的協同過濾推薦演算法時，才有了較大的感觸，在協同過濾中稀疏矩陣產生的背景是，例如下表是某寶N個使用者對購買商品的評分，因為某寶的商品特別多，所以各個使用者之間的交集就小了，此時便產生了稀疏矩陣

        那麼下面我們針對稀疏矩陣做以下總結和討論

二：什麼是稀疏矩陣？

        數值為0的元素數目遠遠多於非0元素的數目，並且非零元素的分佈沒有規律的矩陣稱為稀疏矩陣（sparse），

        其實往往對於稀疏矩陣的定義並沒有明確的規則或者標準，更大程度上是根據人的經驗準則來進行判斷的。

三：為什麼要對稀疏矩陣進行壓縮儲存以及主要的壓縮儲存的方式？

        由於稀疏矩陣中存在大量的“空”值，佔據了大量的儲存空間，而真正有用的資料卻少之又少，且在計算時浪費資源，所以要進行壓縮儲存以節省儲存空間和計算方便。

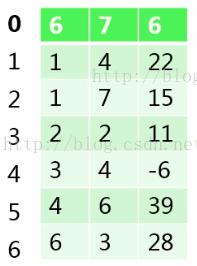
        拿下面這個圖來舉例

        這裡我們首先採用三元組表示方法來表示稀疏矩陣，例如上邊的稀疏矩陣可以表示為：

        (  (1,4,22),(1,7,15),(2,2,11),(3,4,-6),(4,6,39),(6,3,28)  )

       接下來我們討論儲存方式

       1：順序儲存

             若把稀疏矩陣的三元組線性表按順序儲存結構儲存，則稱為稀疏矩陣的三元組順序表。
　　     順序表中除了儲存三元組外，還應該儲存矩陣行數、列數和總的非零元素數目，這樣才能唯一的確定一個矩陣。

             (1)用一個二維陣列A[0..m,1..3]:Integer

             (2)儲存方法：a[0,1]——總行數，a[0,2]——總列數，a[0,3]——存放非零元素個數

             (3)按行存放：每個非零元素所在行，列數以及值

         順序儲存的缺點：

         與用二維陣列儲存稀疏矩陣比較，用三元組表表示的稀疏矩陣不僅節約了空間，而且使得矩陣某些運算的時間比經典演算法還少，但是在進行矩陣加法，減法和乘法等運算時，有時矩陣中的非零元素的位置和個數會發生很大的變化，如A = A+ B，將矩陣B加到矩陣A上，此時若還用三元組順序表，勢必會為了保持三元組表 “ 以行序為主序”而移動大量的元素

       2：鏈式儲存（即稀疏矩陣的三元連結串列）

       鏈式儲存又可以分為三類：

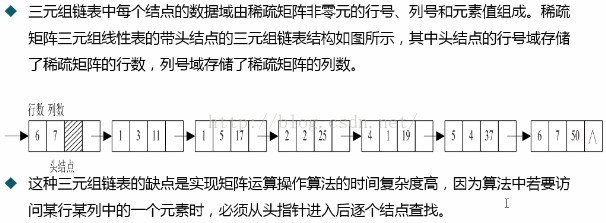
       (1)三元組連結串列：用連結串列儲存的三元線性表

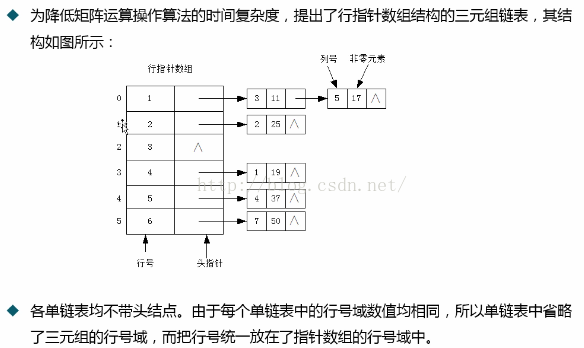
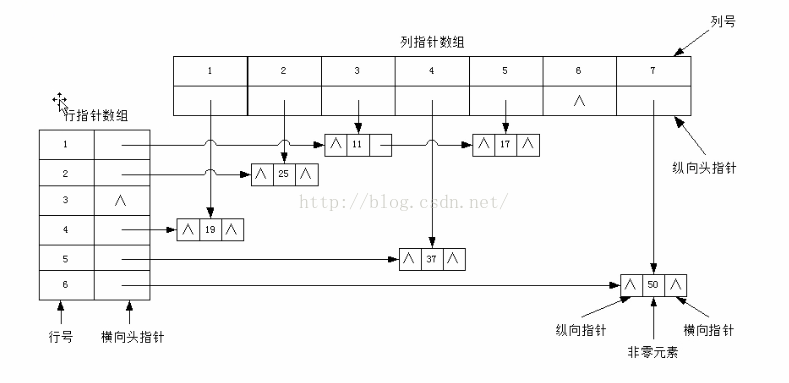
      (2)  行指標陣列結果的三元組連結串列：把每行非零元素三元組組織乘一個單鏈表，再設計一個指標型別的陣列儲存所有單鏈表的頭指標

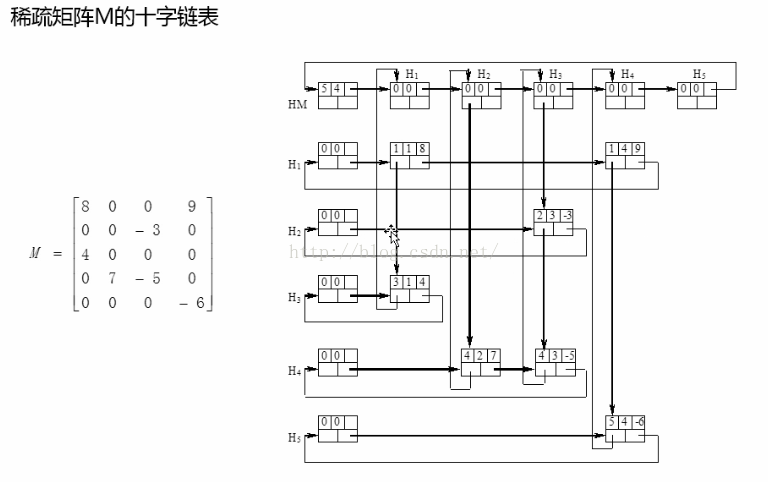
      (3)三元組十字連結串列：用的最多的形式，把非零元素三元組按行和按列組織乘單鏈表，這樣稀疏矩陣的每個非零元素三元組節點都將即勾鏈在行單鏈表上，又都勾鏈在列單鏈表上，形成十字連結串列。

                                 表結點， 行頭結點和列結點，總表頭結點

       3：兩種儲存方式的比較

             三元組順序表：非零元素在表中按行序有序儲存，因此便於進行依行順序處理的矩陣運算，但是，若需按行號存取某一行的非零元素，則需從頭開始進行查詢。（時間複雜度高）

             行邏輯連線的順序表：便於隨機存取任意一行的非零元素

             十字連結串列：當家族很的非零元素個數和位置操作過程中變化較大時，就不適宜採用順序儲存結構來表示三元組的線性表

四：稀疏矩陣的相關運算

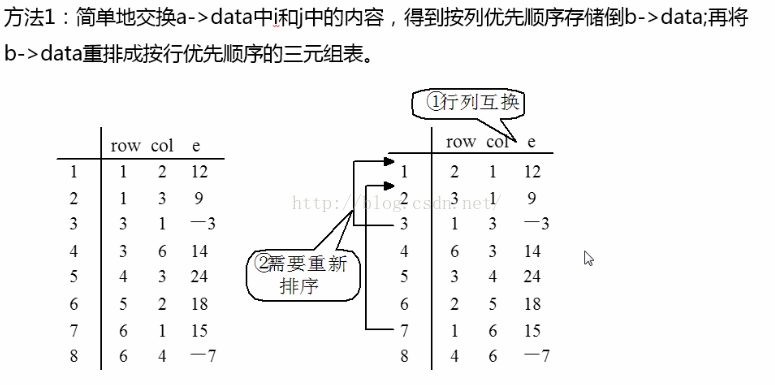
1：轉置

2：基於順序表儲存的稀疏矩陣乘法的實現

前提條件是：前者矩陣的列和後者矩陣的行數目相同，即m*n  n*p，如下兩個矩陣，進行矩陣相乘

其遵循的主要規則是：

                                                C[ i ][ j ] = sum（A[ i ][ k ] * B[ k ][ j ]） (k從1到n)

3：基於兩個十字連結串列儲存的稀疏矩陣的加法

該部分參考：點選檢視

首先矩陣A和B滿足矩陣相加的條件即兩者的行列數相同

已知兩個稀疏矩陣A 和B，分別採用十字連結串列儲存，計算C=A+B，C 也採用十字連結串列方式儲存，並且在A 的基礎上形成C。

由矩陣的加法規則知，只有A 和B 行列對應相等，二者才能相加。C 中的非零元素cij 只可能有３種情況：或者是aij+bij，或者是aij (bij=0)，或者是bij (aij=0)，因此當B 加到A 上時，對A 十字連結串列的當前結點來說，對應下列四種情況：或者改變結點的值（aij+bij≠０），或者不變（bij＝０），或者插入一個新結點（aij＝０），還可能是刪除一個結點（aij+bij＝０）。整個運算從矩陣的第一行起逐行進行。對每一行都從行表的頭結點出發，分別找到A 和B 在該行中的第一個非零元素結點後開始比較，然後按４種不同情況分別處理。

設pa和pb 分別指向A 和B 的十字連結串列中行號相同的兩個結點，４種情況如下：

(1) 若pa->col=pb->col 且pa->v+pb->v≠0，則只要用aij+bij 的值改寫pa 所指結點的值域即可。

(2) 若pa->col=pb->col 且pa->v+pb->v=0，則需要在矩陣A 的十字連結串列中刪除pa 所指結點，此時需改變該行連結串列中前趨結點的right 域，以及該列連結串列中前趨結點的down 域。

(3) 若pa->col < pb->col 且pa->col≠0（即不是表頭結點），則只需要將pa 指標向右推進一步，並繼續進行比較。

(4) 若pa->col > pb->col 或pa->col＝0（即是表頭結點），則需要在矩陣A 的十字連結串列中插入一個pb 所指結點。