人工神經元模型

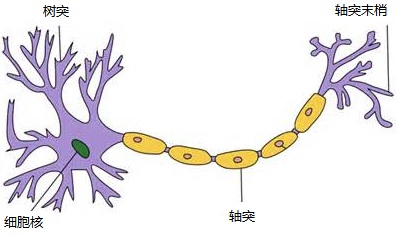
生物學上神經元通常由細胞體，細胞核，樹突和軸突構成。

樹突用來接收其他神經元傳導過來的訊號，一個神經元有多個樹突；

細胞核是神經元中的核心模組，用來處理所有的傳入訊號；

軸突是輸出訊號的單元，它有很多個軸突末梢，可以給其它神經元的樹突傳遞訊號。

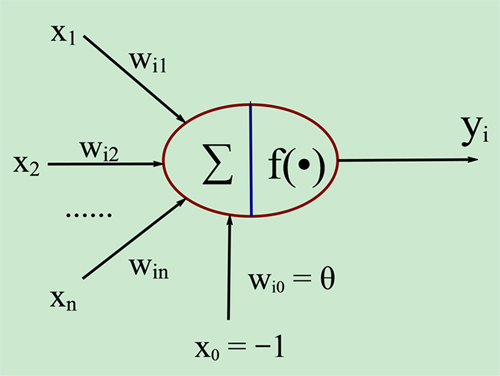
人工神經元的模型可以由下圖來表述：

圖中X1~Xn是從其它神經元傳入的輸入訊號，Wi1~Win分別是傳入訊號的權重，θ表示一個閾值，或稱為偏置（bias），偏置的設定是為了正確分類樣本，是模型中一個重要的引數。神經元綜合的輸入訊號和偏置（符號為-1~1）相加之後產生當前神經元最終的處理訊號net，該訊號稱為淨啟用或淨激勵（net activation），啟用訊號作為上圖中圓圈的右半部分f（*）函式的輸入，即f(net)； f稱為啟用函式或激勵函式

常見的啟用函式

1.  Sigmoid

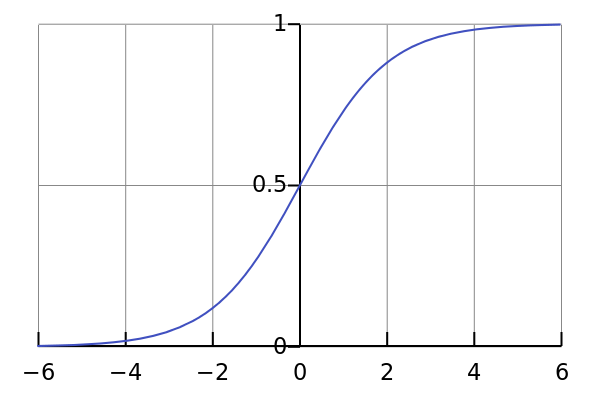
Sigmoid函式的特點是會把輸出限定在0~1之間，如果是非常大的負數，輸出就是0，如果是非常大的正數，輸出就是1，這樣使得資料在傳遞過程中不容易發散。

Sigmod有兩個主要缺點，一是Sigmoid容易過飽和，丟失梯度。從Sigmoid的示意圖上可以看到，神經元的活躍度在0和1處飽和，梯度接近於0，這樣在反向傳播時，很容易出現梯度消失的情況，導致訓練無法完整；二是Sigmoid的輸出均值不是0，基於這兩個缺點，SIgmoid使用越來越少了。

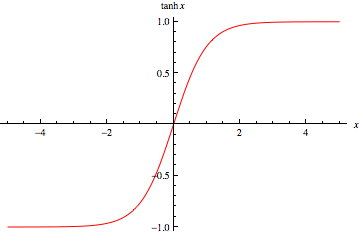
2. tanh

tanh是Sigmoid函式的變形，tanh的均值是0，在實際應用中有比Sigmoid更好的效果。

3. ReLU

ReLU是近來比較流行的啟用函式，當輸入訊號小於0時，輸出為0；當輸入訊號大於0時，輸出等於輸入。

ReLU的優點：

1. ReLU是部分線性的，並且不會出現過飽和的現象，使用ReLU得到的隨機梯度下降法（SGD）的收斂速度比Sigmodi和tanh都快。

2. ReLU只需要一個閾值就可以得到啟用值，不需要像Sigmoid一樣需要複雜的指數運算。

ReLU的缺點：

在訓練的過程中，ReLU神經元比價脆弱容易失去作用。例如當ReLU神經元接收到一個非常大的的梯度資料流之後，這個神經元有可能再也不會對任何輸入的資料有反映了，所以在訓練的時候要設定一個較小的合適的學習率引數。

4. Leaky-ReLU

相比ReLU，Leaky-ReLU在輸入為負數時引入了一個很小的常數，如0.01，這個小的常數修正了資料分佈，保留了一些負軸的值，在Leaky-ReLU中，這個常數通常需要通過先驗知識手動賦值。

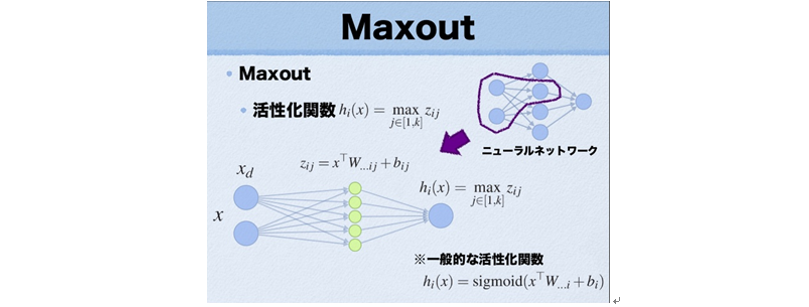
5. Maxout

Maxout是在2013年才提出的，是一種激發函式形式，一般情況下如果採用Sigmoid函式的話，在前向傳播過程中，隱含層節點的輸出表達式為：

其中W一般是二維的，這裡表示取出的是第i列，下標i前的省略號表示對應第i列中的所有行。而在Maxout激發函式中，在每一個隱含層和輸入層之間又隱式的添加了一個“隱含層”，這個“隱隱含層”的啟用函式是按常規的Sigmoid函式來計算的，而Maxout神經元的啟用函式是取得所有這些“隱隱含層”中的最大值，如上圖所示。

Maxout的啟用函式表示為：

f(x)=max(wT1x+b1,wT2x+b2)

可以看到，ReLU 和 Leaky ReLU 都是它的一個變形（比如，w1,b1=0 的時候，就是 ReLU）。

Maxout的擬合能力是非常強的，它可以擬合任意的的凸函式，優點是計算簡單，不會過飽和，同時又沒有ReLU的缺點（容易死掉），但Maxout的缺點是過程引數相當於多了一倍。

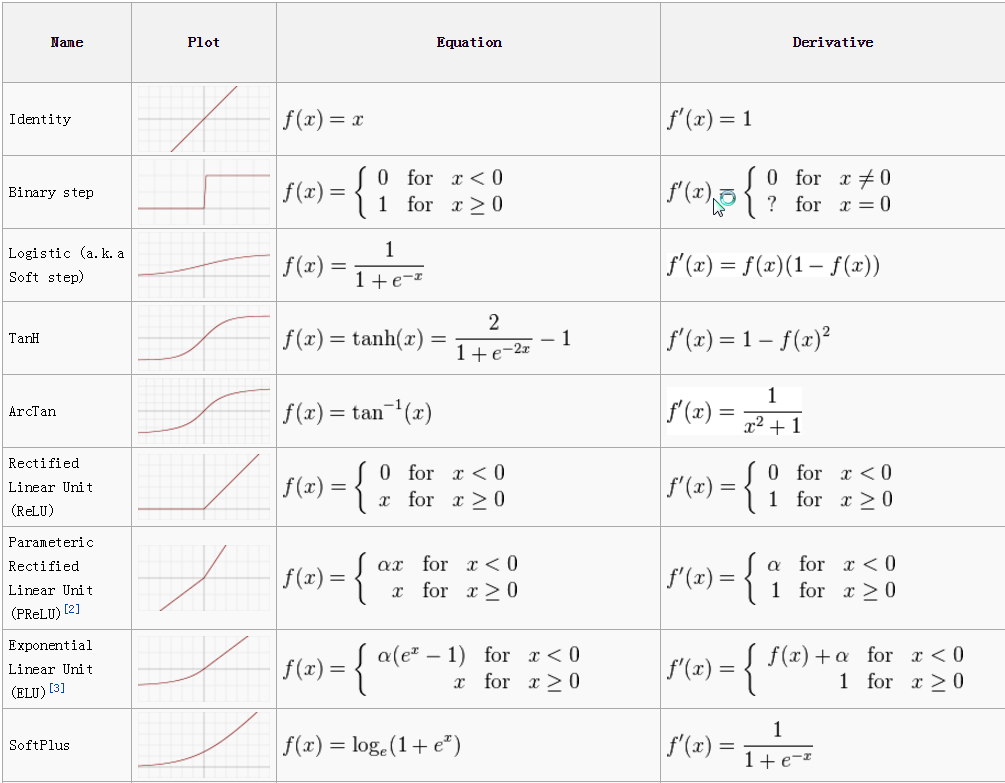
其他一些啟用函式列表：

3. 神經網路模型分類

神經網路由大量的神經元互相連線而構成，根據神經元的連結方式，神經網路可以分為3大類。

(1) 前饋神經網路　(　Feedforward Neural Networks )

前饋網路也稱前向網路。這種網路只在訓練過程會有反饋訊號，而在分類過程中資料只能向前傳送，直到到達輸出層，層間沒有向後的反饋訊號，因此被稱為前饋網路。前饋網路一般不考慮輸出與輸入在時間上的滯後效應，只表達輸出與輸入的對映關係；

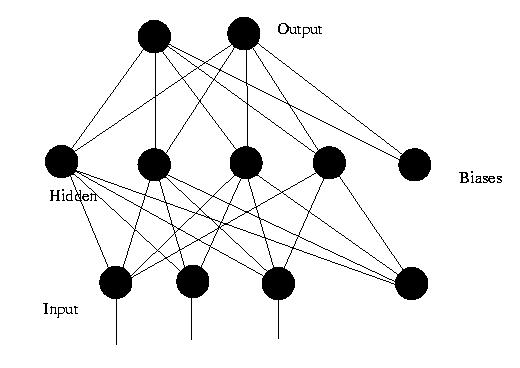
感知機( perceptron)與BP神經網路就屬於前饋網路。下圖是一個3層的前饋神經網路，其中第一層是輸入單元，第二層稱為隱含層，第三層稱為輸出層（輸入單元不是神經元，因此圖中有2層神經元）。

（2）反饋神經網路　(　Feedback Neural Networks )

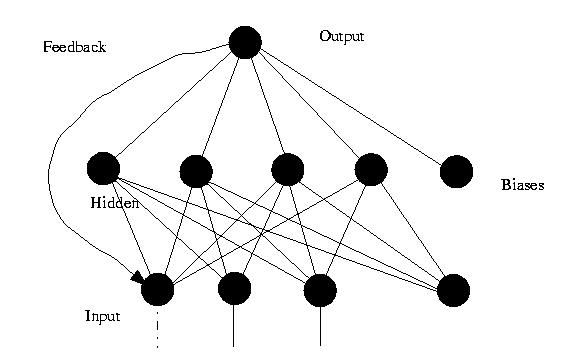
反饋型神經網路是一種從輸出到輸入具有反饋連線的神經網路，其結構比前饋網路要複雜得多。反饋神經網路的“反饋”體現在當前的（分類）結果會作為一個輸入，影響到下一次的（分類）結果，即當前的（分類）結果是受到先前所有的（分類）結果的影響的。

典型的反饋型神經網路有：Elman網路和Hopfield網路。

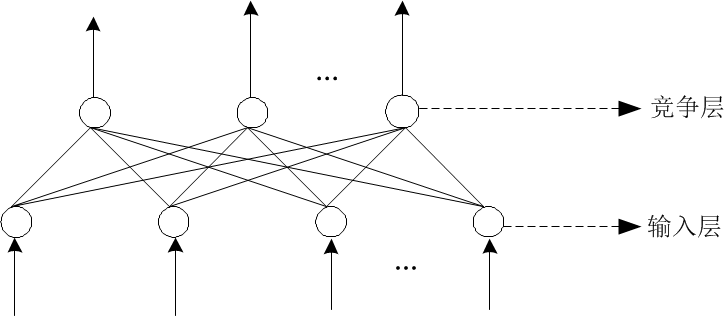
（3）自組織網路 ( SOM ,Self-Organizing Neural Networks )

自組織神經網路是一種無導師學習網路。它通過自動尋找樣本中的內在規律和本質屬性，自組織、自適應地改變網路引數與結構。