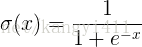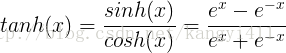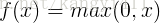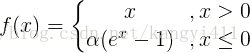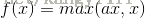注意非線性函式部分（也稱為啟用函式），是神經網路中很重要的一個部分，但是即使我們把非線性函式部分去掉，直接相乘也可以得到類別得分，但是這樣就少了一些擾動（wiggle），影響泛化效能等。 

 Rectified Linear Unit(ReLU) - 用於隱層神經元輸出
Sigmoid - 用於隱層神經元輸出
Softmax - 用於多分類神經網路輸出
Linear - 用於迴歸神經網路輸出（或二分類問題）
 =================================================                          
1. sigmod函式

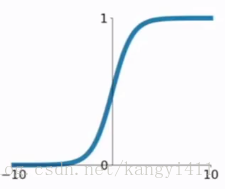
函式公式和圖表如下圖

在sigmod函式中我們可以看到，其輸出是在(0,1)這個開區間內，這點很有意思，可以聯想到概率，但是嚴格意義上講，不要當成概率。sigmod函式曾經是比較流行的，它可以想象成一個神經元的放電率，在中間斜率比較大的地方是神經元的敏感區，在兩邊斜率很平緩的地方是神經元的抑制區。

當然，流行也是曾經流行，這說明函式本身是有一定的缺陷的。

1) 當輸入稍微遠離了座標原點，函式的梯度就變得很小了，幾乎為零。在神經網路反向傳播的過程中，我們都是通過微分的鏈式法則來計算各個權重w的微分的。當反向傳播經過了sigmod函式，這個鏈條上的微分就很小很小了，況且還可能經過很多個sigmod函式，最後會導致權重w對損失函式幾乎沒影響，這樣不利於權重的優化，這個問題叫做梯度飽和，也可以叫梯度彌散。

2) 函式輸出不是以0為中心的，這樣會使權重更新效率降低。對於這個缺陷，在斯坦福的課程裡面有詳細的解釋。

3) sigmod函式要進行指數運算，這個對於計算機來說是比較慢的。

2.tanh函式

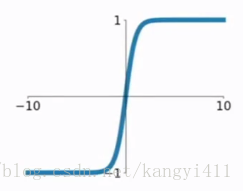
tanh函式公式和曲線如下

tanh是雙曲正切函式，tanh函式和sigmod函式的曲線是比較相近的，咱們來比較一下看看。首先相同的是，這兩個函式在輸入很大或是很小的時候，輸出都幾乎平滑，梯度很小，不利於權重更新；不同的是輸出區間，tanh的輸出區間是在(-1,1)之間，而且整個函式是以0為中心的，這個特點比sigmod的好。

一般二分類問題中，隱藏層用tanh函式，輸出層用sigmod函式。不過這些也都不是一成不變的，具體使用什麼啟用函式，還是要根據具體的問題來具體分析，還是要靠除錯的。

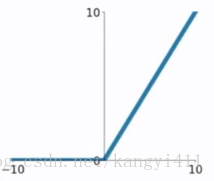
3.ReLU函式

ReLU函式公式和曲線如下

ReLU(Rectified Linear Unit)函式是目前比較火的一個啟用函式，相比於sigmod函式和tanh函式，它有以下幾個優點：

1) 在輸入為正數的時候，不存在梯度飽和問題。

2) 計算速度要快很多。ReLU函式只有線性關係，不管是前向傳播還是反向傳播，都比sigmod和tanh要快很多。（sigmod和tanh要計算指數，計算速度會比較慢）

當然，缺點也是有的：

1) 當輸入是負數的時候，ReLU是完全不被啟用的，這就表明一旦輸入到了負數，ReLU就會死掉。這樣在前向傳播過程中，還不算什麼問題，有的區域是敏感的，有的是不敏感的。但是到了反向傳播過程中，輸入負數，梯度就會完全到0，這個和sigmod函式、tanh函式有一樣的問題。

2) 我們發現ReLU函式的輸出要麼是0，要麼是正數，這也就是說，ReLU函式也不是以0為中心的函式。

4.ELU函式

ELU函式公式和曲線如下圖

ELU函式是針對ReLU函式的一個改進型，相比於ReLU函式，在輸入為負數的情況下，是有一定的輸出的，而且這部分輸出還具有一定的抗干擾能力。這樣可以消除ReLU死掉的問題，不過還是有梯度飽和和指數運算的問題。

5.PReLU函式

PReLU函式公式和曲線如下圖

PReLU也是針對ReLU的一個改進型，在負數區域內，PReLU有一個很小的斜率，這樣也可以避免ReLU死掉的問題。相比於ELU，PReLU在負數區域內是線性運算，斜率雖然小，但是不會趨於0，這算是一定的優勢吧。

我們看PReLU的公式，裡面的引數α一般是取0~1之間的數，而且一般還是比較小的，如零點零幾。當α=0.01時，我們叫PReLU為Leaky ReLU，算是PReLU的一種特殊情況吧。
===================================================

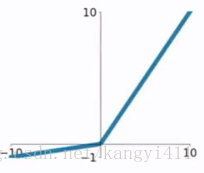
Sigmoid. Sigmoid 非線性啟用函式的形式是，其圖形如上圖左所示。之前我們說過，sigmoid函式輸入一個實值的數，然後將其壓縮到0~1的範圍內。特別地，大的負數被對映成0，大的正數被對映成1。sigmoid function在歷史上流行過一段時間因為它能夠很好的表達“啟用”的意思，未啟用就是0，完全飽和的啟用則是1。而現在sigmoid已經不怎麼常用了，主要是因為它有兩個缺點:

• Sigmoids saturate and kill gradients. Sigmoid容易飽和，並且當輸入非常大或者非常小的時候，神經元的梯度就接近於0了，從圖中可以看出梯度的趨勢。這就使得我們在反向傳播演算法中反向傳播接近於0的梯度，導致最終權重基本沒什麼更新，我們就無法遞迴地學習到輸入資料了。另外，你需要尤其注意引數的初始值來儘量避免saturation的情況。如果你的初始值很大的話，大部分神經元可能都會處在saturation的狀態而把gradient kill掉，這會導致網路變的很難學習。
• Sigmoid outputs are not zero-centered. Sigmoid 的輸出不是0均值的，這是我們不希望的，因為這會導致後層的神經元的輸入是非0均值的訊號，這會對梯度產生影響：假設後層神經元的輸入都為正(e.g. x>0 elementwise in ),那麼對w求區域性梯度則都為正，這樣在反向傳播的過程中w要麼都往正方向更新，要麼都往負方向更新，導致有一種捆綁的效果，使得收斂緩慢。 

當然了，如果你是按batch去訓練，那麼每個batch可能得到不同的符號（正或負），那麼相加一下這個問題還是可以緩解。因此，非0均值這個問題雖然會產生一些不好的影響，不過跟上面提到的 kill gradients 問題相比還是要好很多的。

• Tanh. Tanh和Sigmoid是有異曲同工之妙的，它的圖形如上圖右所示，不同的是它把實值得輸入壓縮到-1~1的範圍，因此它基本是0均值的，也就解決了上述Sigmoid缺點中的第二個，所以實際中tanh會比sigmoid更常用。但是它還是存在梯度飽和的問題。Tanh是sigmoid的變形：。

 
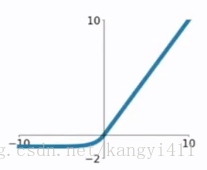
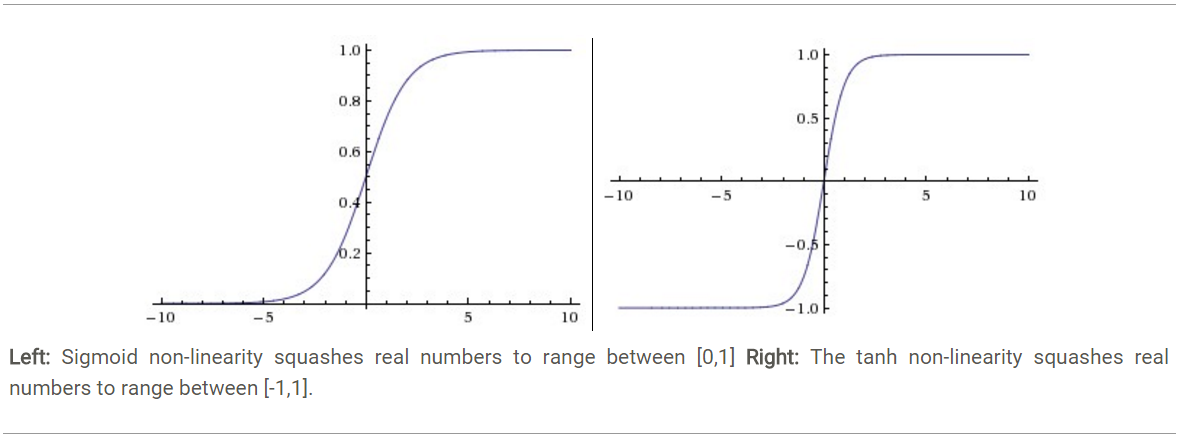
ReLU. 近年來，ReLU 變的越來越受歡迎。它的數學表示式是： f(x)=max(0,x)。很顯然，從上圖左可以看出，輸入訊號 
<0時，輸出為0，>0時，輸出等於輸入。ReLU的優缺點如下：

• 優點1：Krizhevsky et al. 發現使用 ReLU 得到的SGD的收斂速度會比 sigmoid/tanh 快很多(如上圖右)。有人說這是因為它是linear，而且梯度不會飽和
• 優點2：相比於 sigmoid/tanh需要計算指數等，計算複雜度高，ReLU 只需要一個閾值就可以得到啟用值。
• 缺點1： ReLU在訓練的時候很”脆弱”，一不小心有可能導致神經元”壞死”。舉個例子：由於ReLU在x<0時梯度為0，這樣就導致負的梯度在這個ReLU被置零，而且這個神經元有可能再也不會被任何資料啟用。如果這個情況發生了，那麼這個神經元之後的梯度就永遠是0了，也就是ReLU神經元壞死了，不再對任何資料有所響應。實際操作中，如果你的learning rate 很大，那麼很有可能你網路中的40%的神經元都壞死了。 當然，如果你設定了一個合適的較小的learning rate，這個問題發生的情況其實也不會太頻繁。

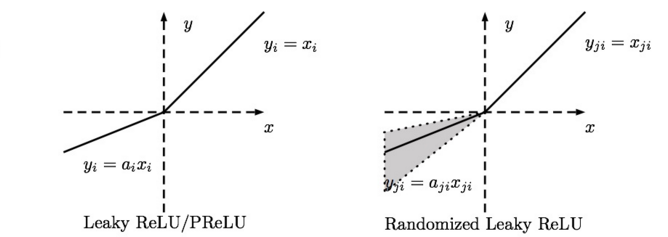
Leaky ReLU. Leaky ReLUs 就是用來解決ReLU壞死的問題的。和ReLU不同，當x<0時，它的值不再是0，而是一個較小斜率(如0.01等)的函式。也就是說f(x)=1(x<0)(ax)+1(x>=0)(x),其中a是一個很小的常數。這樣，既修正了資料分佈，又保留了一些負軸的值，使得負軸資訊不會全部丟失。關於Leaky ReLU 的效果，眾說紛紜，沒有清晰的定論。有些人做了實驗發現 Leaky ReLU 表現的很好;有些實驗則證明並不是這樣。 
- PReLU. 對於 Leaky ReLU 中的a，通常都是通過先驗知識人工賦值的。然而可以觀察到，損失函式對a的導數我們是可以求得的，可不可以將它作為一個引數進行訓練呢? Kaiming He 2015的論文《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》指出，不僅可以訓練，而且效果更好。原文說使用了Parametric ReLU後，最終效果比不用提高了1.03%. 
-Randomized Leaky ReLU. Randomized Leaky ReLU 是 leaky ReLU 的random 版本, 其核心思想就是，在訓練過程中，a是從一個高斯分佈中隨機出來的，然後再在測試過程中進行修正。 

Maxout. Maxout的形式是f(x)=max(w_1^Tx+b_1,w_2^Tx+b_2)，它最早出現在ICML2013上，作者Goodfellow將maxout和dropout結合後，號稱在MNIST, CIFAR-10, CIFAR-100, SVHN這4個數據上都取得了start-of-art的識別率。可以看出ReLU 和 Leaky ReLU 都是Maxout的一個變形，所以Maxout 具有 ReLU 的優點（如：計算簡單，不會 saturation），同時又沒有 ReLU 的一些缺點 （如：容易飽和）。不過呢Maxout相當於把每個神經元的引數都double了，造成引數增多。 
Maxout的擬合能力非常強，它可以擬合任意的的凸函式。作者從數學的角度上也證明了這個結論，即只需2個maxout節點就可以擬合任意的凸函數了(相減)，前提是”隱含層”節點的個數可以任意多。 

=======================================================================
How to choose a activation function? 怎麼選擇啟用函式呢? 
　　我覺得這種問題不可能有定論的吧，只能說是個人建議。 
　　如果你使用 ReLU，那麼一定要小心設定 learning rate，而且要注意不要讓你的網路出現很多壞死的 神經元，如果這個問題不好解決，那麼可以試試 Leaky ReLU、PReLU 或者 Maxout. 
　　友情提醒：最好不要用 sigmoid，你可以試試 tanh，不過可以預期它的效果會比不上 ReLU 和 Maxout. 
　　還有，通常來說，很少會把各種啟用函式串起來在一個網路中使用的。　

轉自：

1.https://blog.csdn.net/kangyi411/article/details/78969642

2.https://blog.csdn.net/u014365862/article/details/52710698