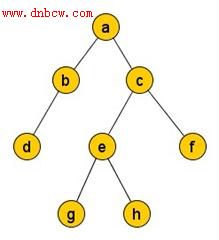
• 類似於層次遍歷
• 首先訪問起始頂點v，
• v出發，依次訪問領接的頂點w1,w2,...,wi

• 不後退，一步可以訪問一批結點

  //結果：abcdefgh

 //演算法：
 bool visited[MAX_VERTEX_NUM]；//訪問標記陣列
 void BFSTraverse(Graph G){
 //圖G進行廣度優先遍歷，設訪問函式visit()
     for(i=0;i<G.vexnum;++i)
         visited[i]=FALSE
     InitQueue(Q);  //初始化輔助佇列
     for(i=0;i<G.vexnum;++i) //從0開始遍歷
         if
 
(!visited[i])     //對每個連通分量呼叫BFS
             BFS(G,i); //vi 未訪問，從vi開始BFS
 }

 void  BFS(Graph G, int v){
     visit(v); // 訪問初始化頂點v
     visited[v]=TRUE; //對v做標記
     Enqueue(Q,v); //頂點v入隊
     while(!isEmpty(Q)){
         DeQueue(Q,v); //頂點v出佇列
         for(w=FristNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)) //檢查v的所有領接點
 

             if(!visited[w]) //w是尚未檢查的頂點
                 visited(w); //訪問頂點
                 visited[w]=TRUE; //標記w
                 EnQueue(Q,w); //頂點w入佇列
     }
 }

• 複雜度
  藉助佇列工作：空間複雜度：O(|V|)
  領接矩陣：查詢每個頂點的時間複雜度是O(|v|2)
  領接表：查詢的時間(O(|E|)),訪問的時間O(|v|); 總時間=O（|V|+|E|）

迷宮最短路徑

• 給定一個大小是N*M的迷宮，每一步向領接的上下左右四格的通道移動。請求出從起點到終點所需的最小步數
  限制條件：N,M<=100

* 輸入
N=10，M=10
#： 牆壁；.:通道； S：起點 G：終點 
#S########
......#..#
.#.##.##.#
.#........
##.##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#

輸出：22

• 演算法：
  
  1. 有近及遠的順序操作
  2. 將訪問過的狀態標註
  3. d[N][M]陣列表示最短距離

#include <stdio.h>  
#include <string.h>  
#include <queue>  
using namespace std;  

struct node  
{  
    int x,y,step;  
};  

char map[105][105];  
int vis[105][105];  
int to[4][2]= {1,0,-1,0,0,1,0,-1};  
int n,m,sx,sy,ex,ey,ans;  

int check(int x,int y)  
{  
    if(x<0 || x>=n || y<0 || y>=m)  
        return 1;  
    if(vis[x][y] || map[x][y]=='#')  
        return 1;  
    return 0;  
}  

void bfs()  
{  
    int i;  
    queue<node> Q;  
    node a,next;  
    a.x = sx;  
    a.y = sy;  
    a.step = 0;  
    vis[a.x][a.y]=1;  
    Q.push(a);  
    while(!Q.empty())  
    {  
        a = Q.front();  
        Q.pop();  
        if(map[a.x][a.y]=='E')  
        {  
            ans = a.step;  
            return ;  
        }  
        for(i = 0; i<4; i++)  
        {  
            next = a;  
            next.x+=to[i][0];  
            next.y+=to[i][1];  
            if(check(next.x,next.y))  
                continue;  
            next.step=a.step+1;  
            vis[next.x][next.y] = 1;  
            Q.push(next);  
        }  
    }  
    ans = -1;  
}  

int main()  
{  
    int t;  
    scanf("%d",&t);  
    while(t--)  
    {  
        scanf("%d%d",&n,&m);  
        int i,j;  
        for(i = 0; i<n; i++)  
            scanf("%s",map[i]);  
        for(i = 0; i<n; i++)  
        {  
            for(j = 0; j<m; j++)  
            {  
                if(map[i][j]=='S')  
                {  
                    sx = i;  
                    sy = j;  
                }  
            }  
        }  
        memset(vis,0,sizeof(vis));  
        bfs();  
        printf("%d\n",ans);  
    }  

    return 0;  
}