金鑰交換的過程，是通訊雙方AB協商一個公共金鑰的過程，該過程的輸出是一個金鑰K，這個金鑰K用於接下來的AB間的通訊過程的加解密。

考慮到因特網可以被竊聽，需要一個演算法來保護這個協商過程，確保只有AB知道協商的結果。

很自然大家會想到非對稱加密機制，實際上D-H金鑰交換過程確實比RSA演算法早。

舉個例子：

A使用一個只有他自己知道的整數Sa，B使用一個只有他知道的整數Sb。

如何使用這2個整數協商出來一個A B知道的金鑰K，而其他人C看到這個過程，也無法知道K，除非C擁有Sa和Sb。

DH協商金鑰過程

DH交換選擇一個巨大整數P,和一個基礎數g，構造一個有限迴圈群Group(g,P)。

這個群有這個特色:

TextA = f(g，P，Sa)

TextB = f(g，P，Sb)

同時：f(TextA, P, Sb) = f2( TextB, P, Sa)  而且都等於 K

f是關於公開常數（g， P）的公開演算法，C不知Sa或者Sb的情況下，無法得知K。

如果具有這個形式就可以使用這個K來作為AB的公共金鑰（e.g. 作為AES演算法的金鑰）來通訊：

f(g(a),b) = f(g(b),a) 

RSA演算法如何協商金鑰

那麼在後來的RSA演算法中，如何協商公共金鑰呢？

RSA演算法的特色是什麼呢？

RSA(Text, Ka) = code && RSA(code, Kb) = Text

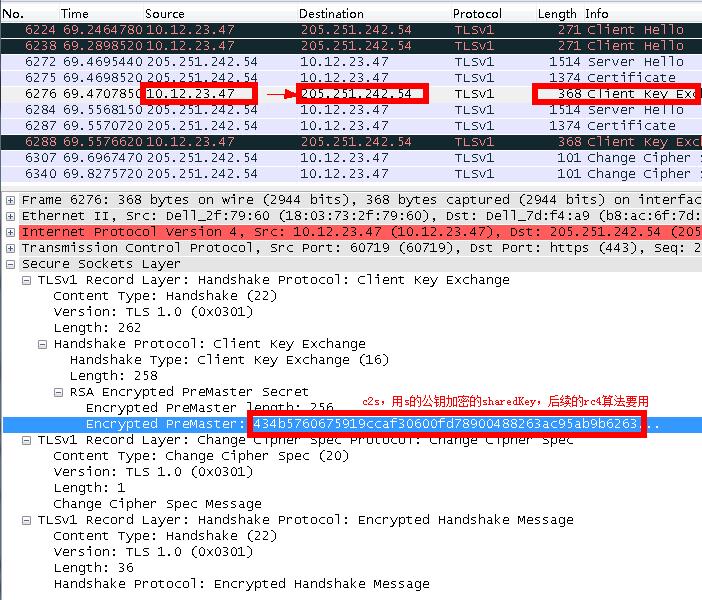
實際上持有公鑰的一方加密一個公共金鑰傳送給持有私鑰的一方就可以了。

RSA(SharedKey, PubKey) = code, RSA(code, PriKey) = SharedKey

DH演算法的缺陷：無法抵禦中間人攻擊

(1) 如果這個時候有個C，在A的uplink上冒充B，在B的uplink上冒充A。

(2) C可以和A協商一個公共金鑰X1， C可以和B協商出來一個金鑰X2。

(3) A傳送的給B的訊息T， f(T1, x1) = c1， C截獲以後，解密得到T1。

(4) C篡改T1，T2 = Hack(T1)。

(5) C 用X2加密 f(T2, X2)=c2, 傳送給B。

(6) B收到訊息c2，解密f(c2, X2) 得到T2，T2是被篡改的T1。

備註：

關於中間人攻擊，實際上，RSA演算法本身也無法抵禦中間人攻擊，比如，如果使用TLS代理伺服器，它實際上就是一箇中間人，所有資訊對它來說都是透明的。

RSA抵禦中間人攻擊，引入了第三方信任機制，通過信任頂層CA，並使用CA簽發它的公鑰和CN，使得中間人無法冒充。

如果DH交換過程中也引入第三方信任機制，也可以解決中間人攻擊問題。