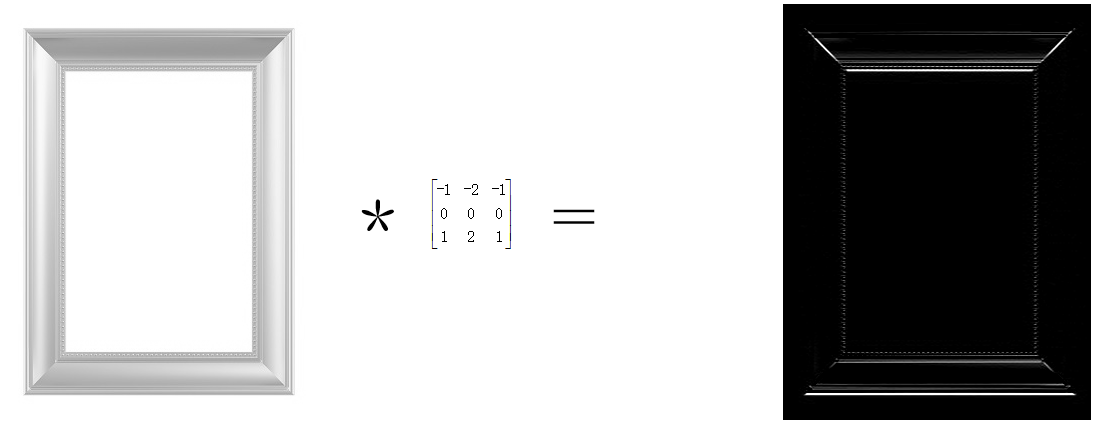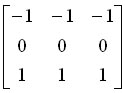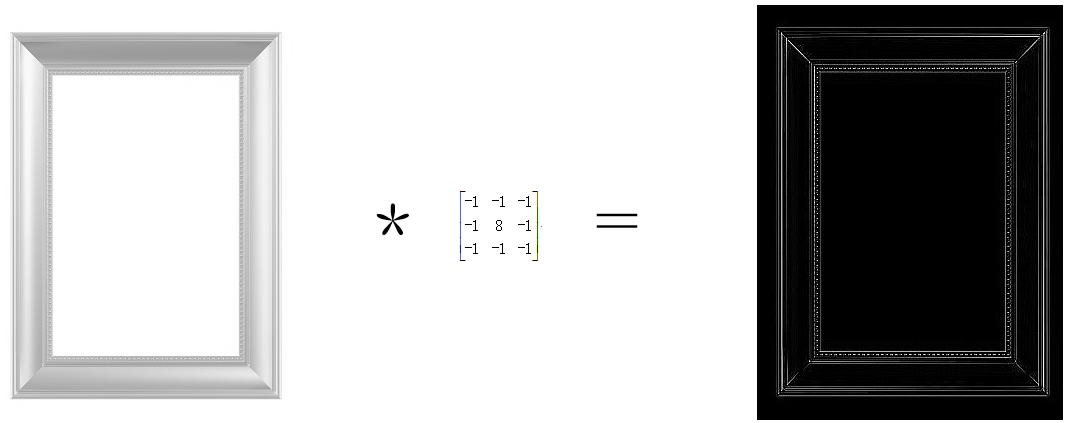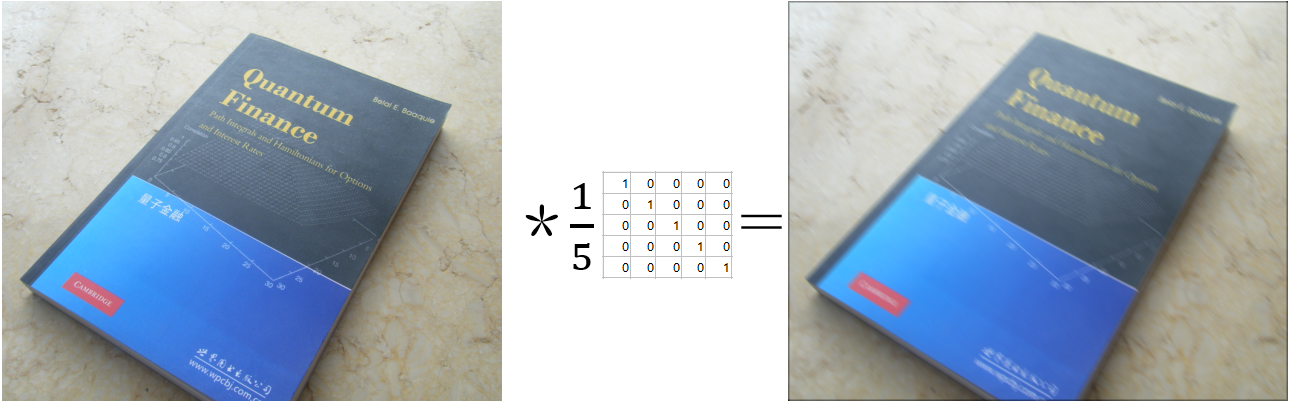影象去模糊（一）——理解模糊核
阿新 • • 發佈：2019-02-19
1、數學模型
當用相機拍攝物體時，物體運動、相機抖動或者物體失焦會造成影象模糊，降低影象的視覺質量。這個過程即為影象退化。影象模糊一般被看作清晰影象卷積模糊核得到模糊影象的過程，其退化模型如下式所示：
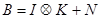
其中，B為模糊影象( blurry image )，I為待估計的清晰影象( latent image )，K為模糊核( blur kernel )，N為附加的噪聲，ⓧ為卷積操作。
2、影象卷積基本概念
2.1 線性濾波
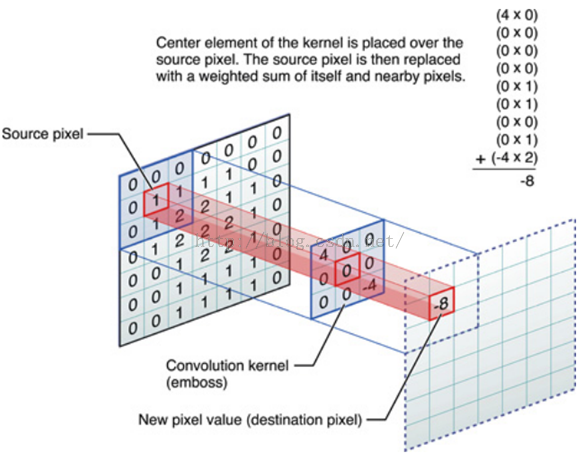
線性濾波是影象處理的基本方法。假設我們有影象矩陣A和濾波器矩陣（卷積核）B，如下圖所示：
對於影象的每一個畫素點，計算它的鄰域畫素和濾波器矩陣的對應元素的乘積，然後加起來，作為該畫素位置的值。這樣就完成了濾波過程。
2.2 卷積與相關
對影象和濾波矩陣進行逐個元素相乘再求和的操作就相當於將一個二維的函式移動到另一個二維函式的所有位置，這個操作就叫卷積或者相關。卷積和相關的差別是，卷積需要先對濾波矩陣進行180的翻轉，但如果矩陣是對稱的，那麼兩者就沒有什麼差別了。
3、模糊核（卷積核）
模糊核實際上就是一個矩陣，清晰影象與模糊核卷積後導致影象變得模糊，因此叫模糊核。模糊核是卷積核的一種。影象卷積操作的本質是矩陣卷積。某些特殊的卷積核會使影象產生特殊的效果。
3.1 邊緣檢測
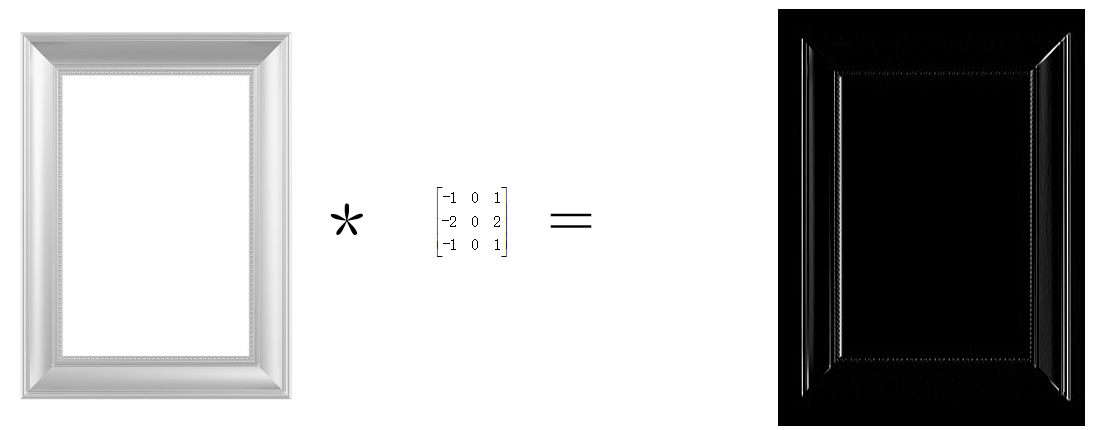
1）Sobel運算元
橫向邊緣檢測：
縱向邊緣檢測：
2）Prewitt運算元
橫向邊緣檢測運算元
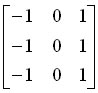。其效果與Sobel運算元幾乎一致，但Prewitt運算元對噪聲相對不敏感。
3）Laplacian運算元
3.2 影象銳化
影象的銳化和邊緣檢測很像，首先找到邊緣，然後把邊緣加到原來的影象上面，這樣就強化了影象的邊緣，使影象看起來更加銳利了。這兩者操作統一起來就是銳化濾波器了，也就是在邊緣檢測濾波器的基礎上，再在中心的位置加1，這樣濾波後的影象就會和原始的影象具有同樣的亮度了，但是會更加銳利。
下面的卷積核更強調邊緣：
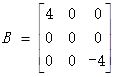
3.3 浮雕
3.4 運動模糊
